График амплитудно – фазовой характеристики (годограф). Частотные характеристики

Задача 1.19. Найти передаточную функцию звена К(р)

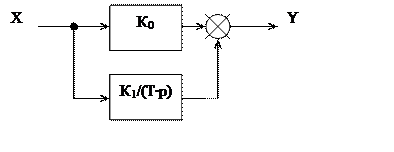Построить график амплитудно – фазовой характеристики (годограф) при К₀ = 10, К₁ = 2, Т = 1 с.

Решение.

Передаточная функция звена определяется суммой передаточных функций безинерционного и интегрирующего звена.

К(р) = К₀ + К₁/(Т∙р) = (К₀∙Т∙р + К₁)/(Т∙р)

тогда

К(jω) = (К₀∙Т∙ jω + К₁)/(Т∙ jω) помножим и поделим на число, комплексно сопряженное со знаменателем

К(jω) = [ - jω∙(К₀∙Т∙ jω + К₁)]/[- jω∙(Т∙ jω)] = (ω²∙К₀∙Т – jω∙К₁)/( ω²∙Т) =

= К₀ – j[К₁/( ω∙Т)] откуда частотные характеристики звена

К(ω) = √Re(K(jω))² + Im(K(jω))²

φ(ω) = arctg[Im(K(jω))/Re(K(jω))]

графики частотных характеристик

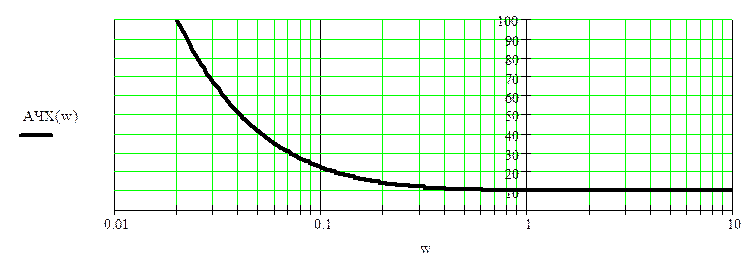
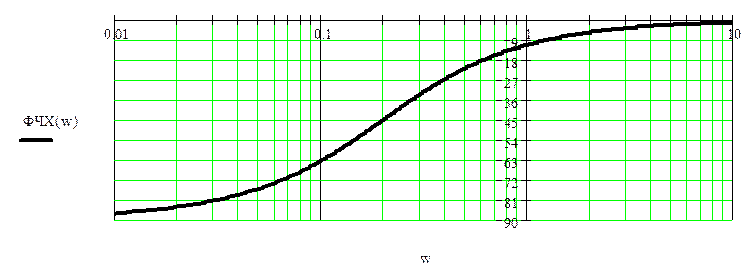
Используя комплексную передаточную функцию цепи изобразим амплитудно – фазовую характеристику цепи.

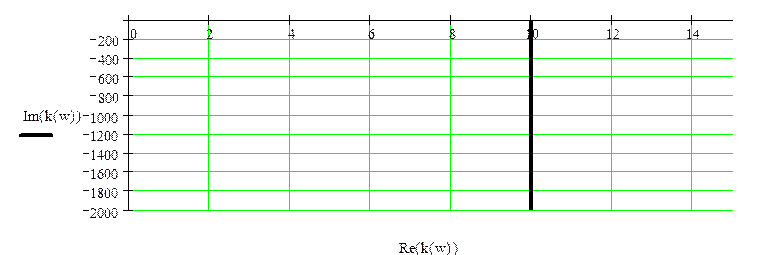
функция представляет собой прямую, исходящую из точки (10; -∞) – при частотах близких к нулю, и заканчивающейся в точке (10; 0) – при частотах близких к ∞. Это объяснятся значительным влиянием на низких частотах интегрирующего звена, а на высоких частотах влиянием безинерционного звена.