Структурная схема следящей системы и преобразованная структурная схема. Оптимальные значения параметров

1)        Структурная схема следящей системы и преобразованная структурная схема:

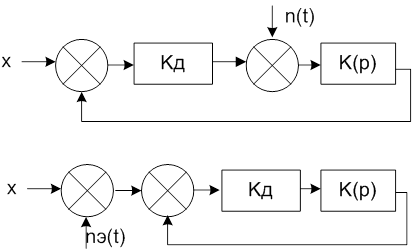
Где Кд – коэффициент передачи дискриминатора, В/Гц; К(р) – передаточная функция фильтра. Вторая схема получается из первой по правилу переноса сумматора с выхода на вход звена при преобразовании спектральной плотности шума: Nэ=No/Кд², где [No]=Вт/Гц.

Передаточная функция разомкнутой цепи:

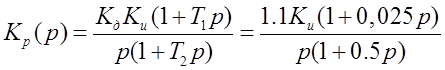
Передаточная функция замкнутой цепи:

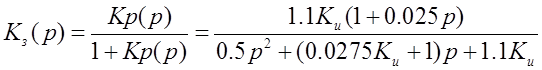
Спектральная плотность эквивалентных флуктуаций, приведенных ко входу дискриминатора:

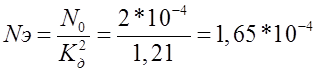
2)        Задача – оптимизировать систему по параметру Ки, т.е. найти такой параметр Ки, при котором достигается минимум величины:

при заданной структуре.

Динамическая ошибка, обусловленная инерционностью следящей системы по отношению к меняющемуся задающему воздействию(порядок астатизма системы равен единице):

, .

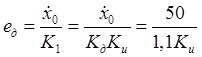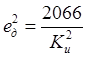Дисперсия шумовой ошибки, обусловленная помехой n(t):

,

где 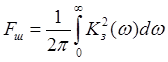 - шумовая полоса следящей системы,  - АЧХ замкнутой системы.

, ,

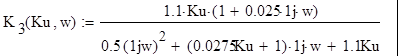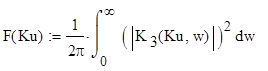Зависимость  ( ^___, …, --- соответственно)от параметра Ки:

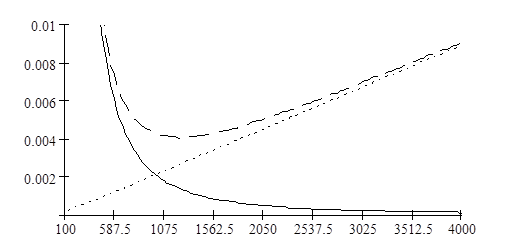 , отсюда оптимальное значение параметра Ки, значение шумовой полосы при оптимальном Ки и квадрат минимально достижимой ошибки слежения:

3)        Передаточная функция разомкнутой цепи при оптимальном параметре:

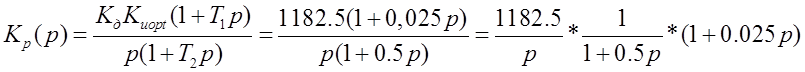
ЛАХ разомкнутой системы (показана сплошной линией):

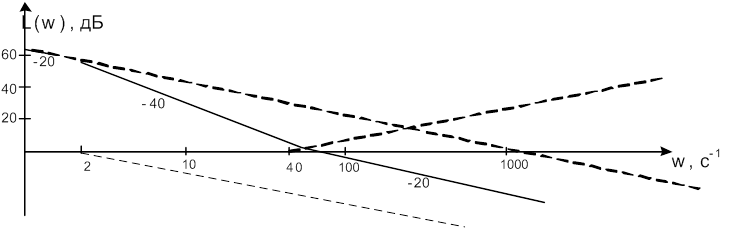
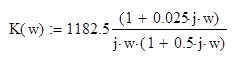
ЛФХ:

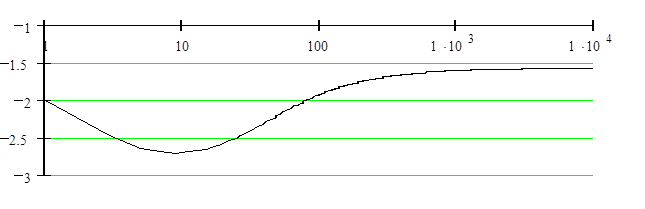
Запас устойчивости по фазе:  - удовлетворительный. Запас устойчивости по амплитуде не определяем, т.к. ЛФХ не пересекает линию -180гр., а от Ки не зависит.

4)        Моделирование следящей системы на ЭВМ. Дискретная передаточная функция цифровой модели следящей системы получается из передаточной функции замкнутой непрерывной системы Кз(р) путем замены оператора непрерывного интегрирования 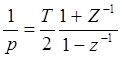, где Т – интервал дискретизации, выбираемый из условия: T<1/2Fш. Т=1/(2*14,306)=0,0035.

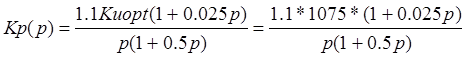
при подстановке

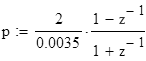 для Ке(z) получим: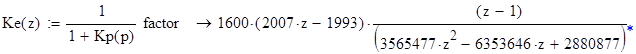

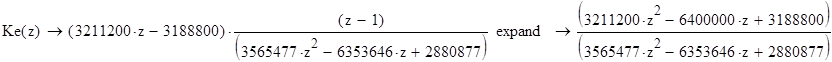
Разделим числитель и знаменатель на z² и после преобразования получим:

,                                   

Отсюда:

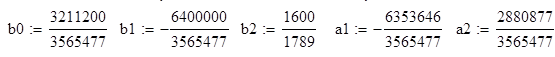
Разностное уравнение запишется в виде:

При единичном воздействии х[k]=1 при к>-1

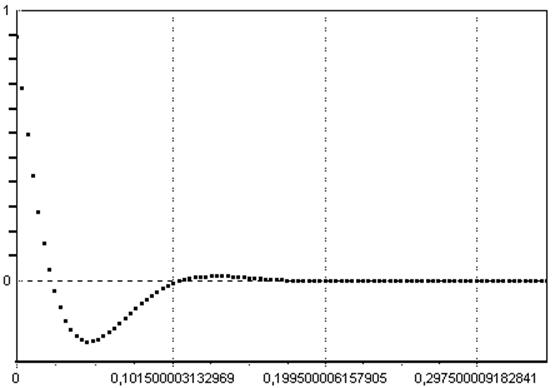
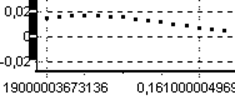
по оси абсцисс – К*Т (с), по оси ординат – значение е(к). Перерегулирование e_max=-0,224=22%, быстродействие (по уровню |е(к)|<0.01) ≈0.161 с.

при линейном воздействии: x[k]=kTx’₀=k*0.0035*50

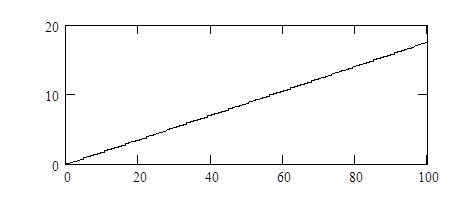
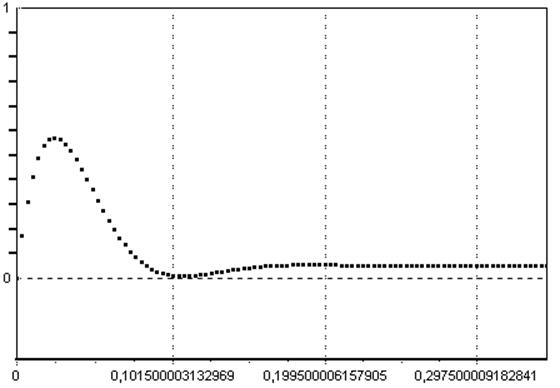
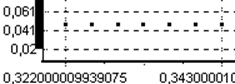
установившаяся ошибка  ≈0,047.