







Федеральное агентство по образованию РФ
Государственное образовательное учреждение высшего профессионального образования
Северо - Западный государственный заочный технический университет
Институт приборостроения и систем обеспечения безопасности
Кафедра метрологии
Учебная дисциплина: Контроль качества
Специальность: 200501
Шифр: 25-0140
2008г.
Задание 1
Необходимо:
- описать вполне реальную информацию, в которой возникает задача синтеза оптимального решения;
- проанализировать априорную информацию с точки зрения её достаточности для синтеза оптимального решения. При необходимости сделать или обосновать необходимые допущения (относящиеся, например, к закону распределения вероятности);
- определить критерий оптимальности, по которому должно быть синтезировано решение;
- сформулировать постановку задачи, обратив особое внимание на требования к качеству решения;
- привести подробные математические выкладки, представляющие собой синтез оптимального решения;
- представить вариант схемотехнической реализации полученного решения; сформулировать предложения по метрологическому обслуживанию устройства;
- прокомментировать результат проделанной работы.
Решение
1. Задача синтеза оптимального решения возникает в нефтепроводном транспорте при фиксации момента и установления факта прохождения внутритрубного объекта (очистного устройства, снаряда дефектоскопа ) по трубопроводу сигнализатором прохождения очистного устройства ДПС-7В. Принцип работы сигнализатора основан на приёме и регистрации акустических шумов, возникающих при движении внутритрубного объекта по трубопроводу в месте его прохождения. Необходимо обнаружить и выделить полезный сигнал на фоне аддитивных помех. Сигнализатор ДПС-7В служит своего рода индикатором для обнаружения акустического сигнала определённой мощности.
2. Проанализируем априорную информацию. Задачей синтеза оптимального решения является обнаружение полезного сигнала на фоне случайных помех, т.е. определение порога обнаружения.
Плотность вероятности мощности помех:
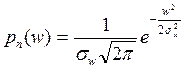 ;
;
Плотность вероятности смеси сигнала с помехами на выходе индикатора:
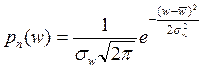
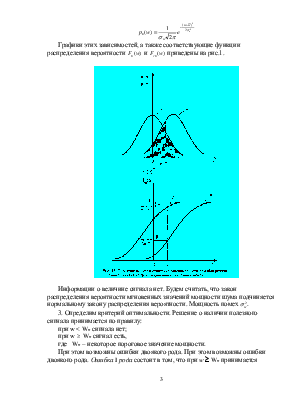
Графики этих зависимостей, а также соответствующие функции распределения
вероятности ![]() и
и ![]() приведены
на рис.1.
приведены
на рис.1.
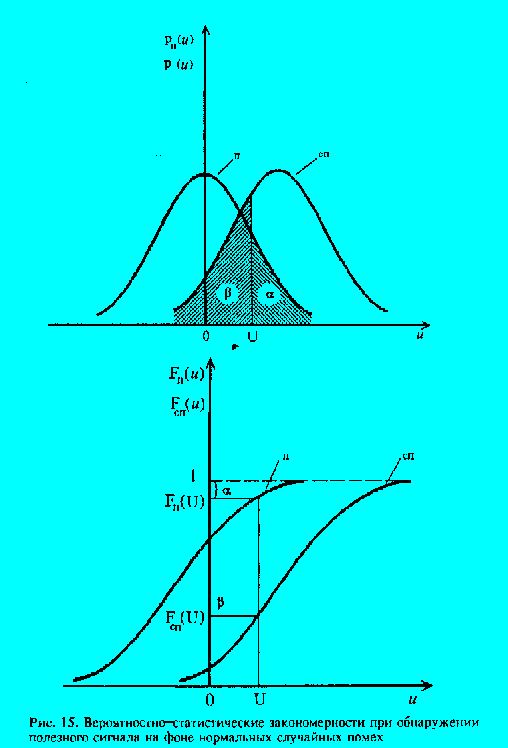
Информации о величине сигнала нет. Будем считать, что закон распределения
вероятности мгновенных значений мощности шума подчиняется нормальному закону
распределения вероятности. Мощность помех ![]() .
.
3. Определим критерий оптимальности. Решение о наличии полезного сигнала принимается по правилу:
при w < Wп сигнала нет;
при w ![]() Wп сигнал есть, где Wп – некоторое
пороговое значение мощности.
Wп сигнал есть, где Wп – некоторое
пороговое значение мощности.
При этом возможны ошибки двоякого рода. При этом возможны ошибки двоякого рода. Ошибка I рода состоит в том, что при w ³ Wп принимается решение «сигнал есть», в то время, как его нет. Вероятность этой ошибки при условии, что сигнала нет, т.е. условная вероятность ошибки I рода:
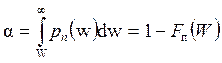 |
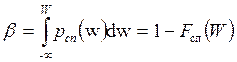 |
Оптимизировать пороговое значение по требованию: ![]() ,
, ![]()
![]() Вт.
Вт.
5. Для решения поставленной задачи необходимо найти
отношение мощности сигнала к мощности помех ![]() .
Решим систему уравнений:
.
Решим систему уравнений:
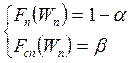 |
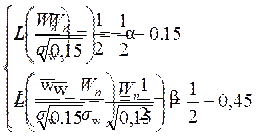 |
Найденное в результате решения первого уравнения значение функции Лапласа подставим во второе уравнение, в результате чего получим:
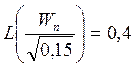
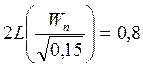
Определим значение функции Лапласа из табл.10 [1].
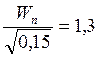 , тогда
, тогда ![]()
6. Представим вариант схемотехнической реализации полученного решения:
Сигнал есть при ![]()
 Сигнала нет при
Сигнала нет при ![]()
7. Вычисленное значение ![]() является
метрологической характеристикой, поэтому следует назначить межповерочный
интервал для проверки: не изменилось ли пороговое значение.
является
метрологической характеристикой, поэтому следует назначить межповерочный
интервал для проверки: не изменилось ли пороговое значение.
Сигнализатор прохождения очистного устройства ДПС-7В, расчётное
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.