Солнце, как основной источник энергии в пределах солнечной системы, страница 2

Ускорение силы тяжести на поверхности Солнца - 274 м/с², т. е. больше земного почти в 30 раз. При этом средняя плотность вещества нашего светила равна 1,41 г/см³. На первый взгляд этот результат кажется удивительным. Ведь масса Солнца так велика, и ускорение на его поверхности большое, - казалось бы, и вещество Солнца должно быть сильно сжато. А на самом, деле средняя плотность его чуть больше, чем у воды, и заметно меньше, чем средняя плотность Земли ρ₎= 5,52_*10³ кг/м³. Причиной этого является низкая молекулярная масса солнечного газа и высокая температура солнечных недр. А что можно сказать о температуре поверхности Солнца? Оказывается, солнечный спектр (смотри

рисунок ІІ.3.1.) довольно близок планковскому спектру равновесного теплового излучения. Эффективная температура поверхности Солнца равна, по различным оценкам - 5770К (5785К). Интересно заметить, что при такой температуре наибольшая энергия излучается как раз в том участке спектра, к которому чувствителен человеческий глаз: в диапазоне длин волн от 400 до 800 нм. Случайно ли это? Вряд ли. Наверное, глаза живых существ и должны приспосабливаться к самому яркому участку спектра окружающего их света.

Для того чтобы более наглядно представить распределение энергии в солнечном спектре рассмотрим данные таблицы ІІ.3.1.

Как видим из таблицы, основная честь энергии Солнца (~92%) сосредоточена в диапазоне длин волн 0,3…3,0 мкм. Именно электромагнитные волны этого диапазона переносят основную часть энергии Солнца, определяющую условия на поверхности планет, тепловой режим КА и т. п. На область длин волн 0,3…0,38 мкм приходится чуть более 6% энергии Солнца, а на область длин волн 0,2…0,3 мкм приходится 1,2…1,4%. Но, как известно, именно излучения ультрафиолетового диапазона длин волн, а его верхней границей можно считать λ = 0,38 мкм, во многом определяют процессы деградации полупроводниковых материалов в ФЭП солнечных батарей КА и коэффициенты лучеиспускания внешних поверхностей КА.

Температура поверхности Солнца определяет, какая энергия во всем спектре приносится солнечными лучами за секунду на единичную площадь, скажем, на квадратный метр земной поверхности, обращенной к Солнцу.

Эта величина (S_◉) очень важна для объяснения земного климата, для проведения расчетов параметров энергетических систем, использующих энергию Солнца и во многих других случаях. Оказывается, что она практически неизменна - поток энергии от Солнца не меняется. Поэтому величину и называют солнечной постоянной. Измерять ее лучше за пределами земной атмосферы, поглощающей часть солнечного излучения. Солнечная постоянная равна 1,36_*10³ Вт/м².

Здесь необходимо небольшое отступление. Дело в том, что Солнечная постоянная для поверхности атмосферы Земли не является постоянной. Она постоянна на поверхности сферы радиусом в 1 а. е., но расстояние от Земли до Солнца, как уже говорилось, испытывает сезонные изменения. Эти сезонные вариации Солнечной постоянной для Земли составляют ± 3,5%. Обусловлены они эллиптичностью земной орбиты. В январе (Земля при этом находится в перигелии) S_◉ = 1,44_*10³ Вт/м², а в июне (Земля при этом находится в афелии) S_◉ уменьшается до 1,36_*10³ Вт/м².

Считая Солнце точечным источником, можно вычислить величину потока его энергии на любом расстоянии

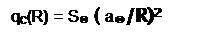где а_◉ = 1,496_*10¹¹ м, R – расстояние на котором определяется q_C(R), т. е. поток энергии Солнца.

Если величину а_◉ подставлять в а. е. то это выражение еще упростится

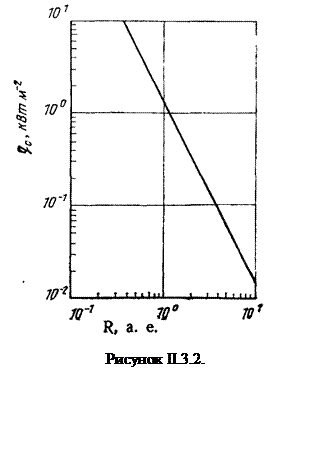
q_C(R) = S_◉*R^-2, но значения R также необходимо переводить в а. е.(см. рисунок ІІ.3.2.).

За секунду Солнце излучает энергию (эта величина называется светимостью Солнца):

L_◉= 4πa²_◉S_◉=3,83_*10²⁶Вт.

Весь поток солнечной энергии проходит, конечно, и через солнечную поверхность. Там плотность потока энергии, т. е. мощность которая излучается квадратным метром поверхности Солнца или, другими словами, яркость Солнца, равна S = L_◉/4πR²_◉ = 6,29.10⁷ Вт/м². Кстати, отсюда, используя закон Больцмана, связывающий плотность потока S с температурой излучающей поверхности, можно вычислить поверхностную температуру Солнца – Т_◉ = (S/σ)^1/4 = 5780 К.