Применение экспертных методов при расчете условной эффективности

15 Застосування експертних методів при розрахунку умовної ефективності. Метод парних переваг

1.3-4.5. Применение экспертных методов при расчете условной эффективности

Под экспертными методами понимают комплекс логических и математико-статистических процедур, предназначенных для получения информации от специалистов, ее последующего анализа и обобщения.

Эксперт при сравнении и оценке возможных вариантов использует определенную систему предпочтения, приписывая каждому из вариантов определенное число.

Рассмотрим основные типы шкал, применяемых при экспертных оценках Номинальная шкала. При сравнении характеристик систем в этой шкале используются понятия «эквивалентно - неэквивалентно» без какой-либо численной оценки сравниваемых характеристик ([А] = [В], [А] ≠[В]).

Порядковая шкала. В отличие от номинальной шкалы в этой шкале, кроме понятия эквивалентности, определяется предпочтительность. Характеристики одной системы перед аналогичной характеристикой другой системы ([А] > [В], [А] < [В]).

Интервальная шкала. В этой шкале, кроме определения предпочтения, дается численная оценка этого предпочтени. определяется, насколько [А] > [В] или [А] < [В]).

Шкала отношения отличается от интервальной шкалы только наличием нулевой точки отсчета.

Для сравнения исследуемых систем необходимо расположить их в порядке возрастания или убывания какого-либо присущего им свойства, или, другими словами, произвести ранжирование.

Ранжированиеприменяется в случаях, когда:

1) необходимо упорядочить какие-либо системы во времени или пространстве, причем интересуются не сравнением степени выраженности какого-либо их качества, а лишь их взаимным расположением;

2) необходимо упорядочить системы в соответствии с каким-либо качеством, которое не может быть точно определено, исходя из практических или теоретических соображений.

При ранжировании эксперт должен расположить системы в порядке, который представляется ему рациональным, и приписать каждому из них числа натурального ряда - ранги.

Если эксперт не всегда в состоянии указать порядок следования для двух или нескольких систем то сумму рангов можно определить сумма рангов S_N, полученная в результате ранжирования n систем, будет равна сумме чисел натурального ряда, т. е.

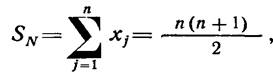                                 где x_j — ранг j-й системы.                                      

Наивысший ранг присваивают системе, получившей наименьшую сумму рангов и, наоборот, системе, получившей наибольшую сумму рангов, присваивают самый низший ранг N. Остальные системы упорядочивают в соответствии со значением суммы рангов относительно системы, которой присвоен первый ранг. Точность и надежность процедуры ранжирования в значительной степени зависит от количества систем: чем систем меньше, тем выше их различимость с точки зрения эксперта.

Метод ранжирования редко используется в чистом виде, чаще всего он сочетается с другими методами, обеспечивающими более четкое различие между системами. Одним из этих методов является метод непосредственной оценки и некоторые его модификации.

Метод непосредственной оценки состоит в том, что диапазон изменения какой-либо переменной разбивается на несколько интервалов, каждому из которых присваивается определенная оценка (балл). Задача эксперта заключается в помещении каждой из рассматриваемых систем или факторов в определенный оценочный интервал в соответствии со степенью обладания тем или иным свойством.

Полученное каждой системой число баллов используется для ранжирования объектов.

1.3-4.5.2. Метод парных сравнений

Суть метода парных сравнений состоит в том, что общая задача экспертизы разбивается на ряд элементарных задач. В каждой элементарной задаче i-й эксперт (i=1, …,m) попарно сравнивает между собой по нескольким показателям важности (S=1,…Q) только два варианта.

Результаты сравнения заносятся в матрицу A^iS размерности J_*J.

Если i-й эксперт оценивает приоритет jי задачи по сравнению с j-й величиной , то важность j-й задачи по отношению к j′-йопределяется выражением

                                           где

Используя усреднение матрицы A^S по всем показателям, вычисляют результирующую матрицу А:

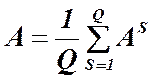
Элементы a_j'j матрицы А называются бифакторными показателями. Конечной целью обработки матрицы А является получение значений приоритетов J систем в виде J - мерного финального вектора, на компоненты которого (т. н. мультифакторные показатели) наложены условия нормировки:

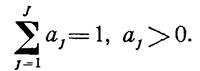
Для построения процедуры перехода от бифакторных оценок к мультифакторным показателям постулируем равенство (т. н. «правило постоянства отношений»)

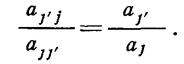
На практике исходные данные являются согласованными весьма приблизительно. Применение описанной выше процедуры для плохо согласованных данных приводит к нарушению условия нормирования. Чтобы избежать этого, необходимо скорректировать исходные данные. Принципиальная возможность такого согласования базируется на том, что дисциплинирующее условие вносит эффект избыточности.Пользуясь правилом согласованности данных, можно построить всю матрицу ω - показателей, если известна только одна ее строка.В качестве сглаживающих преобразователей рекомендуется следующее:

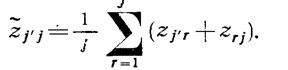Правило согласованности для z-показателей приобретает аддитивный вид:Из матрицы z строится скорректированная матрица по правилуПосле проведения обратного преобразования получаем значение сглаженного ω - показателя: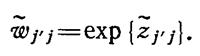

Анализируя эти матрицы, можно увидеть, какие элементарные сравнения являются основными источниками несогласованности и, следовательно, требуют пересмотра.

Недостатком рассмотренного метода является быстрое возрастание числа парных сравнений при увеличении количества оцениваемых задач, что влечет за собой трудности вычислительного и психологического характера.

В связи с этим в случае большой размерности (J > 10) представляется целесообразным разбиение оцениваемых систем по группам. При этом экспертиза проводится в два этапа: между группами и затем внутри групп. Тогда приоритет каждой системы определяется финальным вектором, полученным при проведении сравнения внутри каждой группы и скорректированным в соответствии с оценкой значимости, определяемой финальным вектором сравнения между группами.