Оборудование стендов, контрольная и исследовательская аппаратура стендов для проведения испытаний и отработки ЭРД, страница 7

Примем, что плазма является однородной и оптически тонкой (т. е. отсутствует самопоглощение в объеме самого излучателя). Интенсивность монохроматического излучения, соответствующего спонтанному переходу атомов с верхнего возбужденного уровня s на нижний уровень г, равна

                                  (4.10-11.6.)

где А — эйнштейновский коэффициент спонтанного перехода; N_s — число излучающих атомов, находящихся на верхнем возбужденном энергетическом уровне s; hν — энергия кванта излучения. Уравнение (4.10-11.6.) можно представить так:

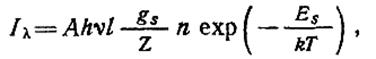                (4.10-11.7.)

где l — толщина излучающего слоя; q_S — статистический вес возбужденного уровня;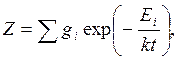 - сумма по состояниям; n - концентрация частиц; E_i - энергия возбуждения уровня; k - постоянная Больцмана; Т - температура.

Для термодинамически равновесной системы Т представляет температуру.

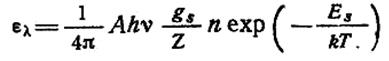              (4.10-11.8.)

Если спектральная линия уширена вследствие линейного эффекта Штарка, то

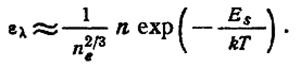                   (4.10-11.9.)

Удобно использовать относительный (нормированный) коэффициент монохроматического излучения, который равен

                      (4.10-11.10.)

где e_λmax — максимальное значение, которое достигается при некоторой температуре Т.

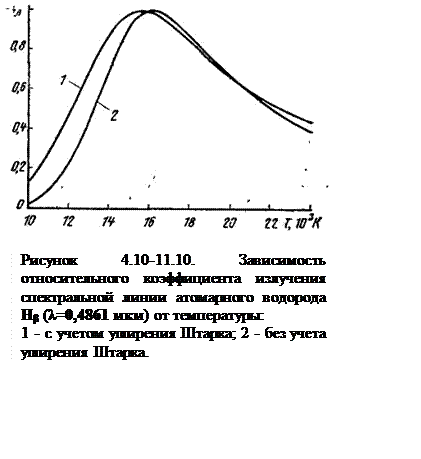
На рисунке 4.10-11.10. приведены зависимости относительного коэффициента излучения спектральной линии атомарного водорода  от температуры для давления 10⁵ Па.

Рассмотрим два простых способа определения температуры термодинамически равновесной системы  (плазмы) по относительной интенсивности спектральных линий. Пусть сравниваются интенсивности I₁ и I₂ двух спектральных линий, которые удовлетворяют уравнению (4.10-11.7.). Тогда температуру можно определить по формуле

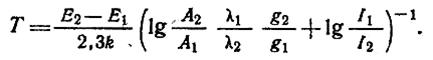                          (4.10-11.11.)

Этот метод широко применяется для определения температуры, например, в электрических дугах.

Поскольку формула (4.10-11.7.) справедлива для оптически тонкого излучателя, то необходима экспериментальная проверка выполнения этого условия. Это можно сделать, если использовать мультиплетные спектральные линии, для которых Е_S≈ const. Отношение спектральных интенсивностей таких спектральных линий не зависит от температуры и является постоянной величиной.

Если излучатель действительно является оптически тонким, то расчетное и экспериментальное значения отношения интенсивностей мультиплетных спектральных линий совпадают.

Для определения распределения температуры Т в осесимметричном оптически тонком излучателе по радиусу г применяется метод, основанный на сопоставлении расчетного нормированного значения  и экспериментально найденного .

Этот метод вначале был применен в астрофизике и получил название — метод максимума функций. Затем он был использован для определения распределения температуры в плазмотронах. Зависимость вычисляется аналитически. Экспериментальное распределение  можно получить на основании известного наблюдаемого значения спектральной интенсивности I_λ(у), используя интегральное уравнение Абеля или обращение уравнения Абеля.

При этом поперечное сечение излучателя разбивается на ряд кольцевых зон.

Численные методы решения уравнения Абеля (или его обращения) основаны на решении систем линейных уравнений. Составлены таблицы коэффициентов таких линейных уравнений для различного числа кольцевых зон, а также разработаны программы расчета  на ЭВМ. Чтобы получить I_λ(у), часто применяют фотографический способ регистрации спектра. Для этого с помощью оптической системы на щели коллиматора спектрографа получают резкое изображение исследуемого объекта. В этом случае оптическая ось спектрального прибора перпендикулярна оси излучателя. Метод фотографической фотометрии позволяет получить изменение интенсивности спектральной линии по высоте излучателя.

Следует обратить внимание на два важных обстоятельства:

во-первых, для спектральных исследований должны применяться прецизионные, стигматические спектральные приборы;

во-вторых, необходимо, чтобы  достигал максимального значения, но не на оси излучателя. Выполнение второго условия позволяет приписать этому радиусу излучателя температуру, которая отвечает максимуму .