ПРИМЕРЫ
варианта тестового задания по теме «Теория вероятностей и математическая статистика»
|
Вариант1 |
Вариант 2 |
|
1. В партии из 12 телефонных аппаратов 5 неисправных. Случайным образом отобрали три аппарата. Найти вероятность того, что 2 из них исправны. ответ |
1. В урне находятся 6 белых и 8 черных шаров. Найти вероятность того, что из четырех шаров, взятых наудачу из урны, половина белых. ответ |
|
2. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос, равна 0,9, на второй – 0,85, на третий – 0,8. Найти вероятность того, что студент ответит не менее чем на два вопроса ответ |
2. Среди вырабатываемых рабочим деталей в среднем 2% бракованных. Найти вероятность того, что среди взятых наугад шести деталей будет: а) три бракованные; б) хотя бы одна бракованная. ответ |
|
3. С первого завода на склад поступает 10% деталей, со второго – 20%, остальные детали – с третьего. В продукции первого завода брак составляет 1%, второго – 0,5%, третьего – 0,2%. Какова вероятность того, что взятая наугад со склада деталь оказалась бракованной? ответ |
3. Вероятность решить контрольную работу для учеников 6 «А» класса равна 0,8, а для учеников 6 «Б» класса – 0,9. В 6»А» учится 30 человек, в 6»Б» - 20. Случайно выбранная контрольная работа оказалась решена верно. Какова вероятность того, что она выполнена учеником 6 «А» класса? ответ |
|
4. Устройство состоит из трех независимых элементов. Вероятность отказа одного элемента равна 0,1. Случайная величина X – число отказавших элементов. Найти: 1) закон распределения СВ X; 2) математическое ожидание M(X); 3) функцию распределения F(x). ответ |
4. Вероятности успешной сдачи каждого из трех экзаменов равны, соответственно, 0,5, 0,6 и 0,7. Случайная величина X – число сданных экзаменов. Найти: 1) закон распределения СВ X; 2) математическое ожидание M(X); 3) функцию распределения F(x). ответ |
|
5. Дана функция распределения F(x) непрерывной случайной величины X
Найти: 1) плотность распределения вероятностей f(x); 2) математическое ожидание M(X); 3) дисперсию D(X); 4) вероятность попадания СВ Х на отрезок [0;1]. ответ |
5. Дана функция распределения F(x) непрерывной случайной величины X
Найти: 1) плотность распределения вероятностей f(x); 2) математическое ожидание M(X); 3) дисперсию D(X); 4) вероятность попадания СВ Х на отрезок [-2;3]. ответ |
Ответы и указания к решению:
Вариант1
1. 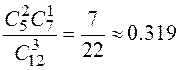 (классическая вероятность – «человечек»).
(классическая вероятность – «человечек»).
2. ![]() («не мене чем на два вопроса» – значит, на
два или три вопроса; теоремы сложения и умножения вероятностей).
(«не мене чем на два вопроса» – значит, на
два или три вопроса; теоремы сложения и умножения вероятностей).
3. ![]() (формула полной вероятности).
(формула полной вероятности).
4. 1) Ряд распределения (вероятности во второй строке посчитаны с помощью формулы Бернулли)
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,729 |
0,243 |
0,027 |
0,001 |
2) М(Х)=3
3) 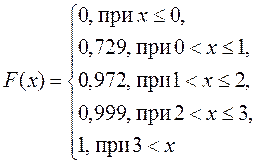
Вернуться к задачам
5. 1)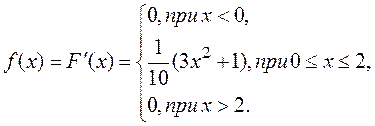
2) 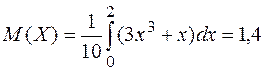 (вспомнить
таблицу интегралов и формулу Ньютона–Лейбница);
(вспомнить
таблицу интегралов и формулу Ньютона–Лейбница);
3) 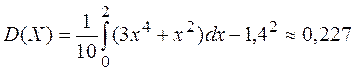 ;
;
4) 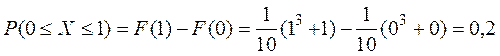 .
.
Вернуться к задачам
Вариант 2
1.
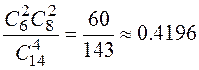 (классическая вероятность – «человечек»).
(классическая вероятность – «человечек»).
2.
а) ![]() (формула Бернулли);
(формула Бернулли);
б) противоположное событие – «из шести нет ни одной бракованной»,
следовательно, ![]() .
.
3.
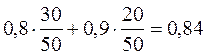 – вероятность того, что контрольная
решена верно (формула полной вероятности). А затем по формуле Байеса
– вероятность того, что контрольная
решена верно (формула полной вероятности). А затем по формуле Байеса 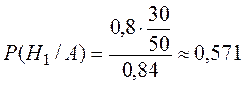
4. 1) Ряд распределения (вероятности во второй строке посчитаны с помощью теорем сложения и умножения вероятностей)
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,06 |
0,29 |
0,44 |
0,21 |
2) М(Х)=1,8
3) 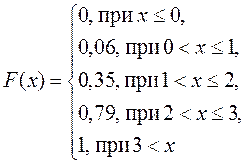
Вернуться к задачам
5.
1)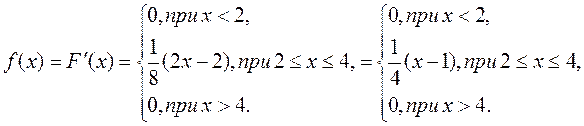
2) 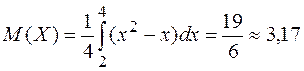 (вспомнить
таблицу интегралов и формулу Ньютона–Лейбница);
(вспомнить
таблицу интегралов и формулу Ньютона–Лейбница);
3)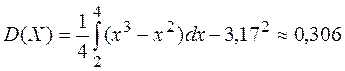 ;
;
4)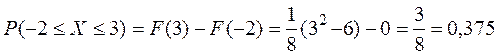
Вернуться к задачам
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.