
























длины вектора ![]() на косинус угла
на косинус угла ![]() между направлением вектора и направлением
оси:
между направлением вектора и направлением
оси:
![]() .
.
Если угол ![]() – острый, то
– острый, то ![]() , если
, если ![]() – тупой , то
– тупой , то ![]() .
.
Определение. Координатами
вектора ![]() называются проекции этого вектора на
координатные оси
называются проекции этого вектора на
координатные оси ![]() Пишут
Пишут ![]() ,
где
,
где
![]() .
.
Если ![]() – углы вектора
– углы вектора ![]() с
осями координат
с
осями координат
(рис. 2.4), то
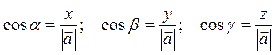 и
и
![]() , где
, где ![]() .
.
сos ![]() называются направляющими косинусами
вектора
называются направляющими косинусами
вектора ![]() .
.
![]() z
z
 |
γ ![]()
β
![]()
 y
y
α
х
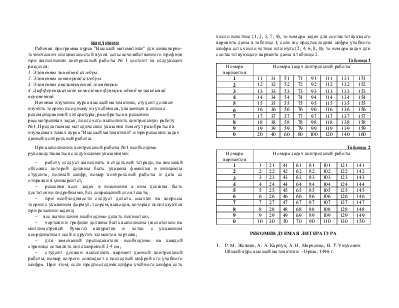
2.3. Скалярное, векторное и смешанное произведение векторов
|
Название |
Определение, свойства, формулы |
Рисунки, комментарии |
||||||||||||||||||||||||||
|
произведение
Смешанное произведение |
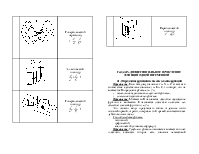
Скалярным произведением векторов
Свойства скалярного произведения: 1.
2. 3. 4. Скалярное произведение
единичных векторов (ортов) (рис. 2.6) удовлетворяет равенствам: Если то Угол между
векторами
Условие коллинеарности векторов
Условие перпендикулярности векторов
Механический смысл скалярного произведения. Работа А постоянной силы
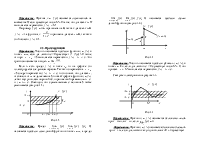
Векторным
произведением
векторов 1. 2. 3. Свойства векторного произведения: 1. 2. 3. 4. Если
|
0
Рис. 2.5 Из рис. 2.5 видно,
что
Поэтому z
х Рис. 2.6
Рис. 2.7 правая тройка векторов т. е. при наблюдении из конца вектора (см. рис. 2.7)
О
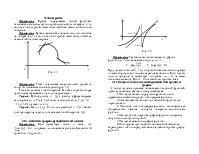
Рис. 2.8 Площадь треугольника
Рис. 2.9
Рис. 2.10 Объём пирамиды
|
||||||||||||||||||||||||||
Пример. Найти
проекцию вектора ![]() на
направление вектора
на
направление вектора ![]() .
.
Решение. Для нахождения проекции используем формулу
![]()
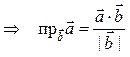 .
.
Векторы заданы координатами, следовательно, скалярное произведение находится по формуле:
![]() .
.
Для нахождения длины вектора ![]() используем формулу
используем формулу
![]() .
.
Значит 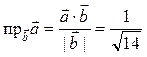 .
.
Пример.
Дан треугольник с вершинами ![]() ,
, ![]() ,
, ![]() . Найти
длину вектора
. Найти
длину вектора ![]() и величину угла
и величину угла ![]() .
.
Решение. Находим координаты вектора ![]() :
:
![]()
![]() .
.
Тогда
![]() .
.
Для
нахождения величины угла С необходимо составить векторы ![]() и
и ![]() :
:
![]() =
=![]() ,
, ![]() =
=![]() .
.
Тогда
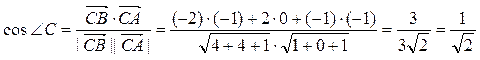 .
.
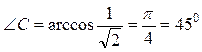 .
.
Пример. Вычислить площадь треугольника с вершинами
![]() ,
, ![]() ,
, ![]() .
.
Решение. Находим координаты вектора ![]() и
и
![]() :
:
![]()
![]() ,
, ![]()
![]() .
.
Вычислим векторное произведение
![]()
![]()
![]() =
=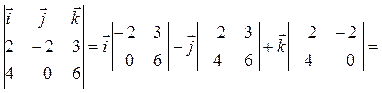
![]() .
.
Воспользуемся
формулой нахождения площади треугольника построенного на векторах ![]() и
и ![]() :
:
![]() .
.
Пример.
Точка ![]() твердого тела закреплена. В точке
твердого тела закреплена. В точке ![]() приложена сила
приложена сила ![]() . Найти
момент силы относительно точки
. Найти
момент силы относительно точки ![]() .
.
Решение.
Вектор ![]() имеет координаты
имеет координаты ![]() .
Вращающий момент находим по формуле:
.
Вращающий момент находим по формуле:
![]()
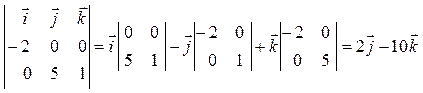 .
.
Пример. Вычислить объём пирамиды с вершинами
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение.
Находим вектора ![]() ,
,
![]()
![]() ,
, ![]()
![]() .
.
Вычислим смешанное произведение этих векторов:
![]()
![]()
![]() =
=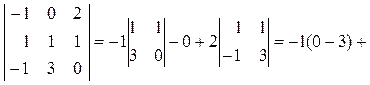
![]() .
.
Объём пирамиды вычисляется по формуле
![]() |
|![]()
![]()
![]() | =
| = ![]() .
.
РазделIII. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
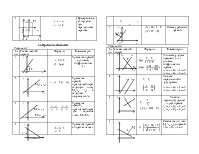
3.1. Простейшие формулы аналитической геометрии
|
№ п/п |
Схематическийчертеж |
Формулы |
Комментарии |
|
|
y B A0 x |
|
Расстояние между двумя точками А(xA, yA) и В(xВ, yВ) |
|
|
y B C A0 x |
|
Деление отрезка в заданном отношении (λ = AC/CB) |
|
|
y B С A0 х |
|
Деление отрезка пополам (λ = 1) |
|
|
y y1 М b 01 x1
0 а х |
|
Преобразования координат при параллельном переносе |
3.2. Прямая на плоскости
|
№ п/п |
Схематическийчертеж |
Формулы |
Комментарии |
|
1 |
y α b 0 x |
|
Уравнение прямой с угловым коэффициентом (k) |
|
2 |
y М0(x0, y0) 0 x |
|
Уравнение прямой, проходящей через заданную точку М0(x0, y0) в заданном направлении (k) |
|
3 |
y М2(x2, y2) М1(x1, y1)0 x |
|
Уравнение прямой, проходящей через две заданные точки М1 и М2. |
|
4 |
y b 0 x a |
|
Уравнение прямой в отрезках на осях |
|
5 |
у
0 x |
|
Общее уравнение прямой |
|
п/п |
Схематическийчертеж |
Формулы |
Комментарии |
|
|
y l1 l2 φ α β 0 x |
|
Угол между двумя прямыми, k1, k 2 – угловые коэффициенты прямых: l1: A1x+ B1y+ C1 = 0 l2: A2x + B2y + C2 = 0 |
|
|
y l1 l2 0 x |
|
Условие параллельности двух прямых l1: A1x+ B1y+ C1 = 0 l2: A2x + B2y + C2 = 0 |
|
|
y l1 l2 0 x |
|
Условие перпендикулярности двух прямых l1: A1x + B1y + C1 = 0 l2: A2x + B2y + C2 = 0 |
|
|
y М0 l d 0 x |
|
Расстояние от точки М0 (x0, y0) до прямой l: Ax+ By+ C = 0 |
|
|
y B A 0 x |
|
Угловой коэффициент прямой, проходящей через две заданные точки А(xА, yА), В(xВ, yВ) |
Пример. Даны вершины треугольника А(– 3; 0), В(4; 2), С(2; –2).
Найти: 1) уравнение стороны АВ; 2) величину угла А; 3) уравнение медианы АМ; 4) уравнение прямой, проходящей через вершину С параллельно стороне АВ; 5) расстояние от точки С до прямой АВ.
Решение. Выберем прямоугольную систему координат и построим треугольник АВС по координатам его вершин.
![]() y
y


![]()
![]() 2
2
![]() В
В
3
![]()

![]() А М 4 х
А М 4 х
1) Воспользуемся уравнением прямой, проходящей через две точки (см. таблицу 3.2, формула 3), получим уравнение стороны АВ:
![]()
![]() .
.
2) Для вычисления ÐА найдём угловые коэффициенты прямых AВ и АС с помощью формулы 5 из таблицы 3.2.
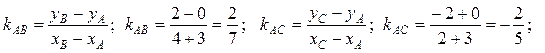 Воспользуемся
теперь формулой 1 из таблицы 3.3 для вычисления угла между двумя прямыми. Угол
А отсчитывается в положительном направлении, поэтому
Воспользуемся
теперь формулой 1 из таблицы 3.3 для вычисления угла между двумя прямыми. Угол
А отсчитывается в положительном направлении, поэтому
![]()
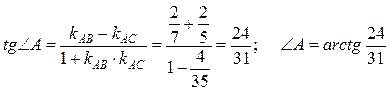 .
.
3) Медиана треугольника – это отрезок прямой, соединяющий вершину треугольника с серединой противоположной стороны. Пользуясь формулой деления отрезка пополам, находим середину ВС:
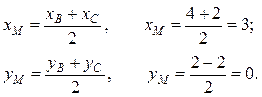
Медиана проходит через две точки А(–3, 0) и М(3, 0), то для записи её уравнения воспользуемся формулой 3 таблицы 3.2.
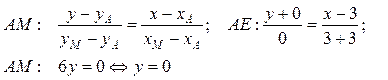
4) Для составления уравнения прямой l, которая проходит через точку С используем тот факт, что её угловой коэффициент равен угловому коэффициенту прямой АВ, т. к. прямые параллельны.
Уравнение прямой АВ, мы уже знаем: ![]() . Найдем угловой коэффициент этой прямой,
для этого выполним преобразования:
. Найдем угловой коэффициент этой прямой,
для этого выполним преобразования:
![]() .
.
Подставив в формулу 2 таблицы 3.2 координаты точки С и угловой
коэффициент ![]() , получим
, получим
![]()
![]()
![]() .
.
5) Для нахождения расстояния от точки С(2,
– 2) до прямой АВ: ![]() воспользуемся формулой 4 из
таблицы 3.3:
воспользуемся формулой 4 из
таблицы 3.3:
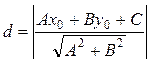
В нашем случаи, ![]() ,
, ![]() ,
следовательно,
,
следовательно,
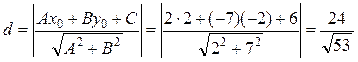
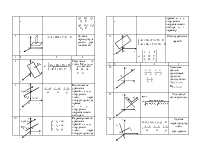
3.3. Плоскость и прямая в пространстве
|
№ п/п |
Схематическийчертеж |
Формулы |
Комментарии |
|||
|
1 |
2 |
3 |
4 |
|||
|
1 |
z 0 у x |
|
Уравнение плоскости, проходящей через заданную точкуМ0(x0, y0, z0) - перпендикулярно заданному вектору
|
|||
|
2 |
z
0 y х |
|
Общее уравнение плоскости |
|||
|
3 |
z M2 M1 M3 0 y x |
|
Уравнение плоскости проходящей через три точки М1(x1, y1, z1), М2(x2, y2, z2), М3(x3, y3, z3) |
|||
|
1 |
2 |
3 |
4 |
|||
|
4 |
z 0 y x |
|
Уравнение плоскости в отрезках на осях, где a, b, c – величины отрезков, отсекаемых плоскостью на координатных осях |
|||
|
5 |
z 0 y x |
|
Угол между двумя плоскостями
|
|||
|
6 |
z 0 y x |
|
Условие параллельности двух плоскостей
|
|||
|
7 |
z 0 y x |
|
Условие перпендикулярности двух плоскостей |
|||
|
1 |
2 |
3 |
4 |
|||
|
8 |
z М0 0 y x |
|
Расстояние от точки М0(x0, y0, z0) до плоскости
|
|||
|
|
z
М0(x0, y0, z0) 0 y x |
|
Канонические уравнения прямой. x0, y0, z0 – координаты точки, через которую проходит прямая; m,
n, p – координаты направляющего
вектора |
|||
|
|
z
М0(x0,y0, z0) 0 y x |
|
Параметрические
уравнения прямой. x0, y0, z0
– координаты точки, через которую проходит прямая; m, n, p – координаты
направляющего вектора |
|||
|
|
z 0 y х |
|
Общие уравнения прямой. |
|||
|
1 |
2 |
3 |
4 |
|||
|
|
z В А 0 y x |
|
Уравнения прямой, проходящей через две данные точки А(x1, y1, z1), В(x2, y2, z2) |
|||
|
|
z
0 y x |
|
Угол между двумя прямыми |
|||
|
|
z
0 y x |
|
Условие перпендикулярности двух прямых |
|||
|
|
z l1 l2 0 y x |
|
Условие параллельности двух прямых |
|||
Пример.Составить
уравнение плоскости, проходящей через точку А(1, 3,
1) и имеющую нормальный вектор ![]() .
.
Решение.Воспользуемся формулой 1 таблицы 3.4.
В
нашем случае, координаты точки, принадлежащей плоскости, равны ![]() , а координаты вектора
, а координаты вектора ![]() =
=
=![]() . Значит общее уравнение плоскости имеет вид:
. Значит общее уравнение плоскости имеет вид:
![]()
![]() .
.
Пример.Составить уравнение плоскости, проходящей через точку А(2, 4, – 1) и отсекающую на осях координат равные положительные отрезки.
Решение.Воспользуемся
формулой 4 из таблицы 3.4, в нашем случае она будет иметь вид 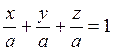 .
.
Т. к. точка А принадлежит нашей плоскости, то можно записать
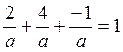 .
.
Решая это уравнение находим, что ![]() .
Следовательно, уравнение плоскости имеет вид:
.
Следовательно, уравнение плоскости имеет вид: 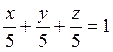 .
.
Пример.Составить уравнения прямой, проходящей через точки А(3, 4, – 1), В(4, 2, 0).
Решение.Воспользуемся формулой 12 таблицы 3.4.
![]()
Пример. Составить параметрические уравнения прямой,
проходящей через точку ![]() параллельно вектору
параллельно вектору ![]() .
.
Решение. Используя формулу 10 из таблицы 3.4, получим требуемые праметрические уравнения прямой
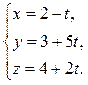
Пример.Найти точку пересечения
прямой 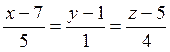 с плоскостью
с плоскостью ![]()
Решение. Представим уравнения прямой в параметрическом виде:
![]()
Откуда ![]()
Подставляя последнии три уравнения в уравнение
плоскости вместо ![]() и
и ![]() ,
получим значение параметра t:
,
получим значение параметра t:
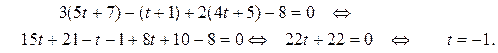
Подставив это значение параметра в параметрические уравнения прямой,
получим координаты точки пересечения прямой и плоскости: ![]()
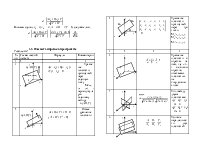
3.4. Перечень основных линий 2-го порядка
|
№ п/п |
Схематическийчертеж |
Каноническое уравнение |
Название линии, комментарии |
|
|
y х |
|
ОкружностьR – радиус окружности; C(а, b) – центр окружности |
|
|
y В А x |
|
Эллипс a – длина большой полуоси, b – длина малой полуоси.
|
|
|
y x |
|
Гиперболаа – длина действительной полуоси; b – длина мнимой полуоси.
|
|
|
y x
у х |
|
Параболар, q – параметр параболы
|
Пример.Исследовать, какая линия определяется уравнением
![]()
Решение.Соберём
члены, содержащие одну и ту же переменную, и из первой скобки вынесем
коэффициент при ![]() , а из второй скобки вынесем
коэффициент при y2,
после чего уравнение примет вид
, а из второй скобки вынесем
коэффициент при y2,
после чего уравнение примет вид
![]()
В каждой из скобок выделим полный квадрат
![]()
или ![]() .
.
Сделав замену: ![]() и
разделив обе части уравнения на 20 получим каноническое уравнение:
и
разделив обе части уравнения на 20 получим каноническое уравнение:
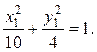
Заданное уравнение
определяет эллипс с полуосями ![]()
центр которого находится в точке О1(– 2, 1).
С помощью параллельного переноса переносим оси
координат в новое начало в точку О1(– 2, 1). В новой системе
координат строим основной прямоугольник со сторонами ![]() стороны
которого параллельны новым осям координат, а центр находится в точке О1.
стороны
которого параллельны новым осям координат, а центр находится в точке О1.
Вписываем в него эллипс.
![]() y1
y1
![]()
![]()
 y
y
x1
·
![]()
![]()

![]() х
х
Рис. 3.1
3.5. Перечень поверхностей 2-го порядка.
|
№ п/п |
Схематический чертеж |
Название поверхностей и их канонические уравнения |
|
1 |
|
Эллипсоид
|
|
2 |
|
Однополостный гиперболоид
|
|
3 |
|
Двуполостный гиперболоид
|
|
|
Конус 2-го порядка
|
|
|
|
Эллиптический параболоид
|
|
|
|
Гиперболический параболоид
|
|
|
|
Эллиптический цилиндр
|
|
|
|
Гиперболический цилиндр
|
|
|
|
Параболический цилиндр
|
Раздел IV. Дифференциальное исчисление функциЙ одной переменной
4.1. Определение функции и способы задания функций
Определение. Если каждому значению хÎ D Ì R ставится в соответствие единственное значение yÎ Е Ì R, то говорят, что на множестве D определена функция y=f(x).
x – независимая переменная или аргумент функции,
y – зависимая переменная или функция.
Определение. Множество D называется областью определения функции, а множество Е называется областью изменения или областью значений функции y= f (x).
Эти области могут представлять собою отдельные точки числовой прямой, отрезки, интервалы этой прямой, множество всех действительных чисел.
Способы задания функции
– табличный,
– графический,
– аналитический (с помощью формул).
Определение. Графиком функции называется множество точек плоскости, абсциссы которых есть значения независимой переменной, а ординаты равны соответствующим значениям функции. Для функции, заданной аналитически, т. е. уравнением
y= f (x), под графиком понимают множество точек М(x, y) плоскости, координаты которых удовлетворяют уравнению y= f (x).
Например, уравнение y = (x– 0,5)2 задает функцию, графиком которой является парабола (рис. 4.1).
![]()

 y
y
![]()
![]()
![]()
0 0,5 x
Рис. 4.1
Функция, заданная аналитически уравнением y = f (x), определена в точке x = x0, если возможно вычислить y0 = f (x0). Множество таких точек образует область определения функции.
Пример. Найти область
определения функции y = ![]() .
.
Решение. Так как арифметический корень определен, когда x2 – – 9 ³ 0, то данная функция определена при x£ – 3 или x³ 3. Областью определения данной функции будет множество
xÎ D = (– ¥; – 3] È [ 3; + ¥).
4.2.Классификация функций
Определение. Основными элементарными функциями называют функции:1. y= xa , aÎ R – степенная;
2. y = ax , a > 0, a≠ 1 – показательная;
3. y = loga x, a > 0, a ≠ 1 – логарифмическая;
4. y = sinx, y = cosx, y = tgx , y = ctgx – тригонометрические;
5. y = arcsinx, y = arccosx, y = arctgx, y = arcctgx обратные тригонометрические функции.
Определение. Функция, заданная последовательной цепью нескольких
функций (y=
f (u), где u= φ(x)),
называется сложной функцией. Например, функция ![]() сложная
и она может быть представлена следующей цепью основных элементарных функций:
сложная
и она может быть представлена следующей цепью основных элементарных функций:
y = z3, z = lg u, ![]() .
.
Определение. Функции, образованные из основных элементарных функций посредством конечного числа алгебраических операций или взятия функции от функции, называются элементарными. Все остальные функции называются неэлементарными. Примером неэлементарной функции может служить функция вида
у = 1 + x+ x2 + … + xn + …
Определение. Неявной называют функцию, которая задана уравнением вида F(x, y) = 0 неразрешенным относительно функции у.
Например, уравнение ![]() задает
неявную функцию у аргумента х.
задает
неявную функцию у аргумента х.
Определение. Если уравнение y = f (x) может быть однозначно разрешено относительно переменной x, т. е. существует функция
x = φ(y), такая что y = f (φ(y)), то функция x = φ(y), или в стандартных обозначениях y = φ(x), называется обратной по отношению к функции y = f (x). Очевидно, что функция y = f (x) обратная по отношению к функции y = φ(x).
Например, для функции y = 2x обратной функцией является функция x = log2 y, или в стандартной форме y = log2 x.
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.
Определение. Функция называется чётной, если ![]() , и нечётной, если
, и нечётной, если ![]() , а область определения симметрична
относительно начала координат.
, а область определения симметрична
относительно начала координат.
График, четной функции симметричен относительно оси Оу, нечётной – относительно начала координат.
Определение. Функция у = ![]() называется
периодической с периодом Т, если
называется
периодической с периодом Т, если ![]() .
.
Определение. Функция у = ![]() называется
ограниченной на множестве Х, если существует число М>
0 такое, что для всех хÎ Х выполняется неравенство | f (x)
| < М.
называется
ограниченной на множестве Х, если существует число М>
0 такое, что для всех хÎ Х выполняется неравенство | f (x)
| < М.
Например, ![]() =
sinx ограничена на R, так как для всех хÎR | f (x) | < 1,
а функция
=
sinx ограничена на R, так как для всех хÎR | f (x) | < 1,
а функция ![]() ограничена для всех x Î R, так как в этой области | f (x)
| £ 2.
ограничена для всех x Î R, так как в этой области | f (x)
| £ 2.
4.3. Предел функции
Определение. Число A называется пределом функции y= f (x) в точке x = x0, если для любого ![]() >0 существует
>0 существует ![]() такое,
что при | x – x0 | < δ выполняется неравенство | f
(x) – A | <
такое,
что при | x – x0 | < δ выполняется неравенство | f
(x) – A | < ![]() . Это кратко записывается
в виде A =
. Это кратко записывается
в виде A = ![]() .
.
Если A есть предел f(x) в точке x0, то на графике это
иллюстрируется следующим образом. Так как из неравенства | x– x0 | < δ
следует неравенство| f (x)
– A | < ![]() , то это
значит, что для всех x, отстоящих от x0 не далее чем
на δ, точка M графика функции y = f (x) лежит
внутри полосы шириной 2
, то это
значит, что для всех x, отстоящих от x0 не далее чем
на δ, точка M графика функции y = f (x) лежит
внутри полосы шириной 2![]() , ограниченной прямыми у=A–
, ограниченной прямыми у=A– ![]() и y = A+
и y = A+ ![]() . Очевидно, что с
уменьшением
. Очевидно, что с
уменьшением ![]() величина δ также уменьшается (см. рис. 4.2).
величина δ также уменьшается (см. рис. 4.2).
![]() y
y![]()
![]()
 А
+ e
А
+ e







![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() А
2ε
А
2ε
Рис. 4.2
Определение. Предел ![]() называется пределом
слева данной функции в точке x = x0, а предел
называется пределом
слева данной функции в точке x = x0, а предел ![]() называется пределом справа данной
функции (см. рис. 4.3).
называется пределом справа данной
функции (см. рис. 4.3).
![]()
![]()

![]()
![]() y
y
![]()
![]() f(x0 + 0)
f(x0 + 0)
f(x0-0)
0 x0 x
Рис. 4.3
Определение. Число A называется пределом функции y
= f(x), в точке x = ± ¥, если для
любого ![]() > 0 существует число
> 0 существует число
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.