Конечная вершина - вершина орграфа, которой инцидентны только заходящие дуги Пример: пусть D - (V,X) - ориентированный граф,
V = {V„V2,J''3}, Х = {х, = {V2,V]},x2 ={V3,Vi}} , тогда V, конечная вершина.
![]() >v
>v
|

Изолированная вершина - вершина, которая не имеет инцидентных ребер.
Пример: пусть D = (V,X) - ориентированный граф,
V = {V,V2,V3.V4}, X = {х, ={V2,V3},х2 ={V3,V2}}, тогда V„ V4 -
изолированные вершины.
Степень вершины - число инцидентных ребер, S(X).
Пример: пусть G = (X.R) - граф, изображенный на рисунке.
Тогда S(х1) = 2. S(х2) = 1, S(x3) = 1 - соответственно степени ^
вершин х1, х2, х3.
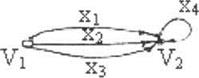 Псевдограф - граф с кратными ребрами
и петлями. Пример: пусть D = (V,X) - ориентированный граф,
X = {х, = {УгУ2},х2={У],У2},х3
={Vl,V2},x4 ={У2,У2}}.
Тогда
D = (У. X) - ориентированный
псевдограф.
Псевдограф - граф с кратными ребрами
и петлями. Пример: пусть D = (V,X) - ориентированный граф,
X = {х, = {УгУ2},х2={У],У2},х3
={Vl,V2},x4 ={У2,У2}}.
Тогда
D = (У. X) - ориентированный
псевдограф.
![]() Пустой граф - граф G = (X,R). в котором R = ф.
Пустой граф - граф G = (X,R). в котором R = ф.
Пример: пусть G = (X,R) - граф, изображенный на рисунке. Он
![]() является пустым, т.к. R = ф, X = {х,,х2,х3}
является пустым, т.к. R = ф, X = {х,,х2,х3}
о
Х2
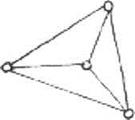 Полный граф
-
граф G = (X.R), в котором любая пара
вершин инцидентна единственному ребру. Обозначается К р, где р = \Х\, гри этом \R\ = 0,5р(р -1).
Полный граф
-
граф G = (X.R), в котором любая пара
вершин инцидентна единственному ребру. Обозначается К р, где р = \Х\, гри этом \R\ = 0,5р(р -1).
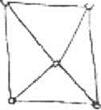
Пример: приведенный на рисунке граф является полным, т.к. это шдно из определения и р = 4, при этом выполняется
Мультиграф - граф. в котором имеются кратные (параллельные) ребра. !3%льтиграф - это псевдограф без петель.
'Пример: пусть D~(V,X) - ориентированный граф, V = {VvV2},
X - {х, = {F,. V2},x2 = {F,,V2}}. Тогда D = (V,X) - ориентированный мультиграф.
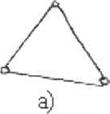
Однородный граф - граф. все вершины которого имеют одну и ту же степень.
Пример: следующие графы, приведенные на рисунке, являются однородными со степенью вершин S(X) = 2. (рис. (а) и (б))
 1
1
1
б)
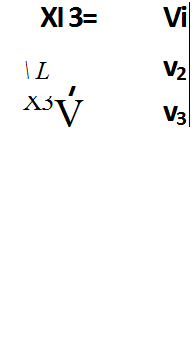

 Матрица смежности - квадратная матрица А = {alt} является матрицей
смежности графа G . если при а. =1 в графе G вершины х, и х;
соединены / ребрами, при а, = 0 вершины х, и х, в G несмежны.
Матрица смежности - квадратная матрица А = {alt} является матрицей
смежности графа G . если при а. =1 в графе G вершины х, и х;
соединены / ребрами, при а, = 0 вершины х, и х, в G несмежны.
Пример: для орграфа D. изображенного на рисунке, приведем матрицу смежности:
v3
Матрица инцидентности орграфа G = (X,R) - прямоугольная матрица М = {тп}, тч = 1 ,если вершина х, является началом дуги г t; тч - -1, если вершина х( является концом дуги г .; тп = 0. если вершина х,
Пример: для орграфа, приведенного в примере для матрицы смежности, составим матрицу инцидентности:
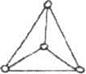
 Два графа G - (X,U) и L- (X',U') являются изоморфными, если между парами
множеств их вершин, ребер и дуг существуют взаимно однозначные соответствия,
сохраняющие смежность и ориентацию для дуг.
Два графа G - (X,U) и L- (X',U') являются изоморфными, если между парами
множеств их вершин, ребер и дуг существуют взаимно однозначные соответствия,
сохраняющие смежность и ориентацию для дуг.
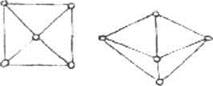
Пример-: следующие графы, приведенные на рисунке, изоморфны:
Маршрут длины Н - чередующаяся последовательность х],u,х2,...,ин,хн+] вершин х, и ребер иj, обладающих тем свойством, что пара соседних элементов инцидентна.
Пример: последовательность VlxtV2x,V1xjV, - маршрут длины соединяющий вершины F, и V* в графе, приведенном на рисунке.
Замкнутый маршрут - маршрут, у которого начальная вершина совпадает с конечной.
|
|||||
|
|||||
Простая цепь - цепь, в которой все вершины различны.
Пример: для ориентированного графа D = (V,X), приведенного выше в примере с цепью,
i]x1l\x4J/3 и Vх2У^х4¥~ - простые цепи из V, в V, длины 2.
Цикл - цепь, у которой начальная и конечная вершина
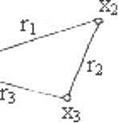 совпадают.
совпадают.
Пример: пусть G = (X,R) - граф, показанный на
Xi
рисунке, тогда х,г,х2г2х?г3х] - цикл.
Простой цикл - простая цепь, у которой концевые вершины совпадают.
|
|||||||
|
|||||||
|
|||||||
|
|||||||
Х4 Гз Хз клеров цикл - это цепь, содержащая все ребра графа в точности один раз. у которой
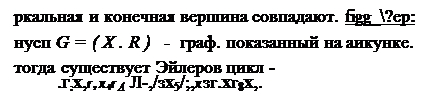 |
|||||||||||||
|
|
||||||||||||
|
|||||||||||||
|
|||||||||||||
|
|||||||||||||
Х4
1ЛЬТОНОВ цикл - это простая цепь.
^ржржлщая все вершины графа, у которой начальная и конечная вершины
совпадают.
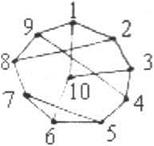
/Пример: приведенный на рисунке граф имеет Гамильтонов * цикл: (10,6,7,5.4,3,2,8.9,1,10).
 Путь (ориентированная
цепь) -
цепь орграфа G . в которой ориентация дуг (ребер)
Путь (ориентированная
цепь) -
цепь орграфа G . в которой ориентация дуг (ребер)
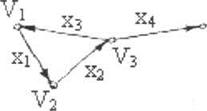
совпадает. пример: для ориентированного графа, приведенного на рисунке, имеем путь из V, в V3 длины 3: V,xlVlx2V2x4V3.
 П ростой путь - путь, не содержащий
повторяющихся вершин. Пример: для ориентированного графа, приведенного
на рисунке, имеем простой путь из V, в V4: VjxlV2x2V3x4V4.
П ростой путь - путь, не содержащий
повторяющихся вершин. Пример: для ориентированного графа, приведенного
на рисунке, имеем простой путь из V, в V4: VjxlV2x2V3x4V4.
Контур - путь, у которого начальная и конечная вершины совпадают.
Пример: для ориентированного графа, приведенного на
рисунке, имеем контур: VlxlFlx2F2x3F2x4F3x5V3x6V]
-ДО хч V2
Простой контур - контур, не содержащий повторяющихся вершин.
Пример: для ориентированного графа, изображенного на рисунке, имеем простой контур: F^x2V3x3F4x4F5x5F2
![]()
 Подграф графа G = (X,R) - граф G’ = {X',R’), для которого X' с! и две вершины в G'
Подграф графа G = (X,R) - граф G’ = {X',R’), для которого X' с! и две вершины в G'
Ч “Y
Пример: пус гь G = (X, R) - исходный граф, показанный на рисунке (а), тогда G' = (X'.R'),- некоторый подграф графа G = (X,R) (рисунок (б))
![]() (б)
(б)
МП

 Су граф графа G = (X.R) - граф G' - (X.R') содержит то же множество
вершин, что и
Су граф графа G = (X.R) - граф G' - (X.R') содержит то же множество
вершин, что и
граф G и R' с R .
Пример: пусть G-(X,R) - некоторый --'Т--.
исходный граф. показанный на рисунке (а), Г~ ~~У «<Г
тогда G' = (X. R') - некоторый суграф графа "
G = (X.R)( б).
О) (б)
Связный граф - граф, у которого любая пара вершин взаимодостижима.
Пример: оба графа, которые были приведены выше в качестве примеров суграфа, являются также связанными графами.
Сильносвязный граф - орграф, у которого любые две вершины взаимодостижимы. Пример: следующие два ориентированных графа, показанных на рисунке, являются сильносвязанными орграфами.
![]()
Компонента связности графа - максимальный подграф графа G . в котором все вершины попарно достижимы.
Пример: у графа, показанного на рисунке, три компоненты связности. ,Д F
/ \ /
Сильная компонента орграфа G максимальный подграф орграфа G , в у. -у_
![]() котором любая пара вершин сильно V-, ц у.-, связана. Vi> \"''"S'
котором любая пара вершин сильно V-, ц у.-, связана. Vi> \"''"S'
Пример: у орграфа, изображенного на j \ / V]*3
 пятнур ТПИ ЬТ\ЛТГТГ>ТТР«Х1.Т Г-МТТТ^НПЙ т-
пятнур ТПИ ЬТ\ЛТГТГ>ТТР«Х1.Т Г-МТТТ^НПЙ т-
vf
Вершина V] ориентированного графа называется достижимой из вершины V2. если существует путь с началом в \\ и концом в V2.
Пример: в приведенном на рисунке орграфе вершина F, является достижимой из вершины F3.
ViX
t V’
![]()
![]() --------------
--------------
V5 V4
Минимальная длина простой цепи с началом в \\ и концом в F, называется расстоянием между этими вершинами.
 Пример: в графе,
изображенном на рисунке, расстояние между вершинами Vi и V] равно трем.
Пример: в графе,
изображенном на рисунке, расстояние между вершинами Vi и V] равно трем.
"Vi
Смешанный граф - это граф, содержащий как дуги, так и ненаправленные ребра. Пример: граф. показанный на рисунке, является смешанным.
XI
Vi^
Х2
- Хз
![]()
![]() N,V4
N,V4
Вершина V инцидентна дуге х тогда и только тогда, когда V является
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.