Расчет размерных цепей сборочных единиц, страница 2

Необходимое количество компенсаторов для каждого размера вычисляют так, как указано в гл. 5.

При этом необходимое количество компенсаторов первой ступени

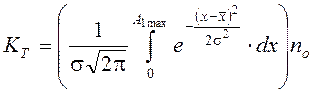, где ; ; 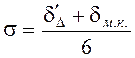 – количество оборотных единиц.

Количество последующих ступеней компенсаторов

.

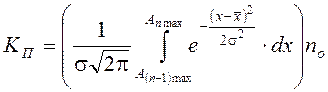Для определения количества компенсаторов последней ступени верхний предел интегрирования следует принимать ¥.

Варианты заданий

Установить допуски и предельные отклонения  на линейные размеры деталей сборочной единицы, представленной на рис. 11.1. Количество сборочных единиц составляет 10000 шт.

Задачу решить методом полной, частичной, групповой взаимозаменяемости, методом регулирования и подгонки: А₁ = 60 мм, А₂ = 85 мм, величина зазора e_р принимается в зависимости от варианта (табл. 11.1)

Таблица 11.1

Исходные данные

Вариант	0	1	2	3	4	5	6	7	8	9	10
e	1–0,2		1–0,16		1–0,12

Решение: (10-й вариант)

Составим схему размерной цепи и определим номинальный размер А₃:

,

, =24 мм.

Составим схему размерной цепи

 

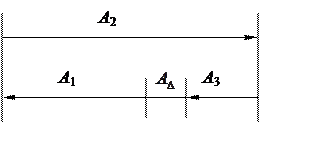Обеспечение точности допуска составляющих звеньев размерной цепи (гл. 6) производится по формулам

;

;

;

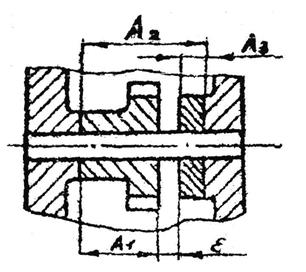
Рис. 11.1. Сборочная единица

Средний квалитет составляющих звеньев

.

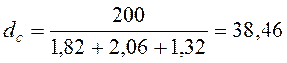Линейные размеры деталей могут быть выполнены с точностью по 9-му квалитету, которому соответствует =40. Предельные отклонения на размеры см. в прил. 2:

А₁ = 60_-0,074, А₂ = 85^+0,087.

Предельные отклонения на размер А₃ определим позднее. Допуск из основного уравнения разменных цепей (гл. 6)

,

Находим координату середины поля допуска на размер А₃:

,

, = –0,0195

Тогда верхнее и нижнее отклонения будут иметь следующие значения:

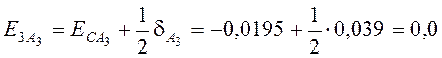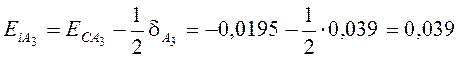  мм,

  мм,

А₃ = 24_-0,039 мм.

Обеспечение точности замыкающего звена методом неполной взаимозаменяемости. Значения единиц допуска составляющих звеньев размерной цепи будут те же, что и при расчете методом полной взаимозаменяемости.

Средний квалитет составляющих звеньев при Р – 0,27 % (гл. 6)

.

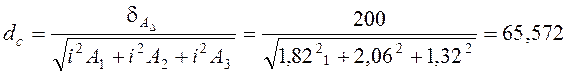Линейные размеры деталей могут быть выполнены с точностью по 10-му квалитету

А₁ = 60_–0,12, А₂ = 85^+0,14.

Предельные отклонения на размер А₃ определим позднее. Допуск из основного уравнения разменных цепей с учетом исходных данных (гл. 6)

.

Находим координату середины поля допуска на размер А₃:

,

, = +0,03.

Тогда верхнее и нижнее отклонения будут иметь следующие значения:

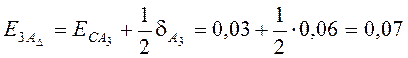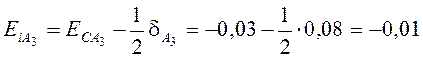  мм,

  мм,

А₃ = 24 мм.

Обеспечение точности замыкающего звена методом групповой  взаимозаменяемости.

Учитывая степень сложности изготовления деталей, примем отклонения размеров по 11-му квалитету для всех составляющих звеньев размерной цепи. Тогда

= 0,19; = 0,22; = 0,13.

Учитывая условия, что допуск увеличивающего звена =+, расчетный допуск замыкающего звена составит

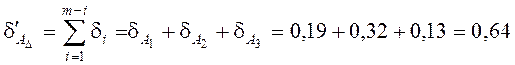 мм.

Число групп, на которые должны быть рассортированы детали после изготовления

.

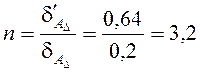Принимаем четыре группы.

При четырех группах величина расчетного допуска ×=4×0,2=0,8. Тогда допуск увеличивающего звена А₂ должен составлять 0,4 мм. Соответственно увеличиваем допуски уменьшающих звеньев, принимая = 0,24, = 0,16 кратным количеству принятых групп.

Для выявления возможных вариантов отклонений у составляющих звеньев размерной цепи приведем возможные отклонения каждого из звеньев (табл. 11.2).

Таблица 11.2

Отклонение звеньев размерной цепи

А1= 60, = 0,24			А2= 85, = 0,40			А3= 24, = 0,16
Еi	ЕS	ЕC	Еi	ЕS	ЕC	Еi	ЕS	ЕC
–0,24	0	–0,120	–0,40	0	–0,20	–0,16	0	–0,08
–0,21	0,03	–0,09	–0,35	0,05	–0,15	–0,14	0,02	–0,06
–0,18	0,06	–0,06	–0,3	0,1	–0,1	–0,12	0,04	–0,04
–0,15	0,09	–0,03	–0,25	0,15	–0,05	–0,10	0,06	–0,02
–0,12	0,12	0	–0,2	0,2	0	–0,08	0,08	0
–0,09	0,15	0,03	–0,15	0,25	0,05	–0,06	0,10	0,02
–0,06	0,18	0,06	–0,1	0,3	0,1	–0,04	0,12	0,04
–0,03	0,21	0,06	–0,05	0,35	0,15	–0,02	0,14	0,06
0	0,24	0,12	0	0,40	0,20	0	0,16	0,08