Задание на РГЗ № 2
по курсу «Уравнения математической физики»
Каждая пара студентов решает по одной задаче из каждой группы. Задачи должны быть решены в системе Matlab. Разрешается использование встроенных средств оформления электронных документов – Notebook. Пример оформления решения таких задач прилагается. Перед выполнением работы каждому студенту необходимо ознакомиться с методикой работы в системе Matlab с помощью литературы (обращаться в читальный зал или абонемент НТБ ГОУВПО «КнАГТУ»), список которой прилагается.
Электронный вариант отчета должен быть продемонстрирован преподавателю, а затем, после его принятия, сброшен в папку ..\All\УМФ группы. Название файла отчета формируется из наименования предмета (УМФ), фамилии и инициалов выполнивших задание (Иванов_ИП_Петров_СА), группы (3ВС_1), номера РГЗ. Все эти пункты разделяются символом подчеркивания, например,
УМФ_Иванов_ИП_Петров_СА_3_ВС_1_РГЗ_1.doc
Каждое задание предполагает изучение соответствующего теоретического материала по литературе. Подразумевается, что студент должен самостоятельно прочитать соответствующий раздел, разобраться с требуемым методом решения, разработать алгоритм, запрограммировать его на известном языке программирования (Matlab) и оформить отчет по выполненной работе, т.е. проявить самостоятельность и творческие качества. Разделы отчета: титульный лист; решение; экранные формы и графики (если есть); список использованной литературы.
Задание
I. Найти в указанной
области отличные от тождественного нуля решения 
дифференциального
уравнения, удовлетворяющее заданным граничным условиям (задача Штурма-Лиувилля):
1)
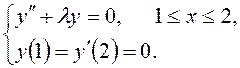
2)
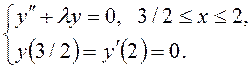
3)
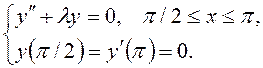
4)
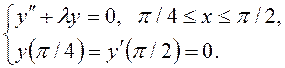
5)
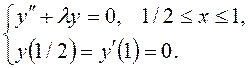
6)
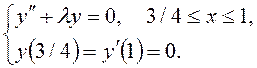
7)
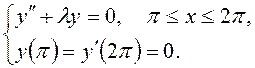
8)
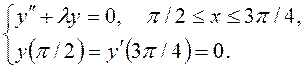
9)
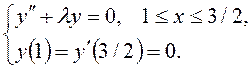
10)
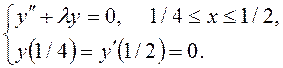
II. Решить задачу Дирихле для уравнения Лапласа в круге.
1) 
, 
, 
.
2) , 
, 
.
3) , , 
.
4) , , 
.
5) , 
, 
.
6) , , 
.
7) , 
, 
.
8) , , 
.
9) , , 
.
10) , , 
.
III. Решить задачу Дирихле для уравнения Лапласа в кольце.
1) , 
, 
, 
.
2) , 
, 
, 
.
3) , , , 
.
4) , , , 
.
5) , , 
, 
.
6) , , 
, 
.
7) , , , .
8) , , , .
9) , , 
, 
.
10) , , 
, 
.
IV. Найти функцию, удовлетворяющую внутри круга уравнению Гельмгольца и принимающую на границе круга заданное значение.
1) 
, , 
.
2) , 
, 
.
3) , , 
.
4) , 
, 
.
5) , 
, 
.
6) , , 
.
7) , , 
.
8) , 
, 
.
9) , 
, 
.
10) , 
, 
.
Литература[1]
по курсу «Уравнения математической физики»
1. Усольцев Ю.Я. Уравнения математической физики: Конспект лекций. Ч. 1 – Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. техн. ун-т, 2001. – 82 с.
2. Усольцев Ю.Я. Уравнения математической физики: Конспект лекций. Ч. 2 – Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. техн. ун-т, 2003. – 59 с.
3. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. – 4-е изд., испр. – М.: ФИЗМАТЛИТ, 2004. – 688 с.
4. Владимиров В.С., Жаринов В.В. Уравнения математической физики: Учебник для вузов. – 2-е изд., стереотип. – М.: ФИЗМАТЛИТ, 2003. – 400 с.
5. Агошков В.И., Дубовский П.Б., Шутяев В.П. Методы решения задач математической физики / Под ред. Г.И. Марчука: Учебное пособие. – М.: ФИЗМАТЛИТ, 2002. – 320 с.
6. Егорова Ю.Г. Некоторые задачи математической физики: Учебное пособие. – Комсомольск-на-Амуре: Комсомольский-на-Амуре гос. техн. ун-т, 2001. – 87 с.
7. Бицадзе А.В. Уравнения математической физики. – М.: Гл. ред. физ.-мат. лит-ры изд. «Наука», 1976 г.
8. Потемкин В.Г. Система Matlab 5 для студентов. – М.: Диалог-Мифи, 1998. – 314 с.
9. Потемкин В.Г. Система Matlab. Справочное пособие. – М.: Диалог-Мифи, 1997. – 350 с.
10.Иглин М. Математические расчеты на базе MATLAB. – М.: 2005.
11.Дьяконов В.П. Matlab 6/6.1/6.5 + Simulink 4.5 в математике и моделировании. – М.: СОЛОН-Пресс, 2003. – 565 с.
12.Дьяконов В.П. Matlab. – СПб: Питер, 2001. – 553 с.
13.Дьяконов В.П. и др. Matlab 5.3.1 с пакетами расширений. – М.: Нолидж, 2001. – 879 с.
14.Лазарев Ю.Ф. Matlab 5.х. – Киев: BHV: Ирина, 2000. – 384 с.
15.Мартынов Н.Н. Matlab 7. Элементарное введение. – М.: КУДИЦ-ОБРАЗ, 2005. – 413 с.
[1] Вся литература по Matlab’у в читальном зале.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
