Интерполяция функций

Министерство образования Российской Федерации

Комсомольский-на-Амуре государственный

технический университет

Факультет компьютерных технологий

Кафедра МОПЭВМ

Лабораторная работа №4.

«Интерполяция функций».

Вариант 20.

Выполнил: Шелестов И.А.

Группа: 4ВС-1

Проверила: Михайлова Н.Н.

Комсомольск-на-Амуре

2006

Задание.

1) По формуле функции f(x) на интервале [-1,1] построить интерполяционные таблицы с равномерным шагом для числа точек n₁ и n_2. Построить интерполяционные полиномы g₁(x) и g₂(x) для числа точек n₁ и n₂. Для контроля распечатать интерполяционные таблицы и значения интерполяционных полиномов g₁(x) и g₂(x) в узлах интерполяции. Для K=l00 построить графики функции f(x) и интерполяционных g₁(x) и g₂(x) на интервале [-1,1], а также найти дискретные аналоги нормы разности интерполяционных полиномов и функции f(x) на интервале [-1,1].

2) По формуле функции f(x) на интервале [-1,1] построить интерполяционную таблицу с неравномерным шагом так, чтобы узлы интерполяции совпадали с нулями полинома Чебышева степени n₂. Построить интерполяционный полином g₃(x) по этой таблице. Для контроля распечатать интерполяционную таблицу и значения интерполяционного полинома g₃(x) в узлах интерполяции. Для К=100 построить графики функции f(x) и интерполяционного полинома g₃(x) на интервале [-1,1], а также найти дискретные аналоги нормы разности интерполяционного полинома g₃(x) и функции f(x) на интервале [-1,1].

Пояснение: интерполяционные полиномы строятся в форме Лагранжа.

Заданная функция.

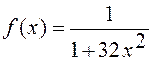,  число шагов:  n1=10, n2=28

Решение.

1. Равномерный шаг

Вычисление узлов интерполяции:

, где ,  , а=  –1, b=1.

Построение интерполяционной таблицы: (x_i,y_i), , y_i=f(x_i)

Построение интерполяционного полинома Лагранжа по формуле:

,  

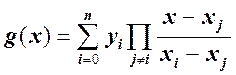Вычисление дискретных аналогов нормы разности интерполяционного полинома и функции по формулам:

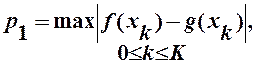       x_kÎ [a ,b] "k :  0 £k£K ;

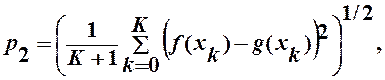     x_kÎ [a ,b] "k :  0 £k£K .

Листинг программы.

// Подключаемые библиотеки

#include <conio.h>

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

#include <graphics.h>

float xmin, xmax;                  // Область изменения x

float ymin, ymax;                  // Область изменения y

float hx;                          // Шаг

float xdens, ydens;

// Вычисление экранной x координаты

int ex(float x,float y)

{return (int) ((x-xmin)/xdens);}

// Вычисление экранной y координаты

int ey(float x,float y)

{return (int) ((ymax-y)/ydens);}

// функция возвращает значение заданной функции

float f (float x) { return 1/(1+32*x*x); }

// функция возвращает значение интерполяционного полинома в форме Лагранжа

float g (float X, float *x, float n)

{

double p,s=0;

for (int i=0; i<=n; i++)

{

p = 1;

for (int j=0; j<=n; j++)

{

if (i==j) continue;

p *= (X-x[j])/(x[i]-x[j]);

}

s += p*f(x[i]);

}

return s;

}

// Построение по формуле функции f(x) интерполяционной таблицы размер// ности n+1. Интерполяци с постоянным шагом

// Массив x - узлы интерполяции,

// Массив y - значения функции f(x) в узлах сетки.

// Массив z - значения интерполяционного полинома

void xyz (float n, float *x, float *y, float *z, float a, float b)

{

float h=(b-a)/n;

for (int i=1; i<=n; i++)

x[i] = -1+i*h;

for (i=0;i<=n;i++)

y[i] = f(x[i]);

for (i=0; i<=n; i++)

z[i] = g(x[i],x,n);

printf ("\t   x        y(x)        g(x)\n");

for (i=0; i<=n; i++)

{

if (i==18)  // при заполнении страницы ждем нажатия клавиши

{

printf ("Для продолжения нажмите любую клавишу...\n");

getch ();

printf ("\t   x        y(x)        g(x)\n");

}

printf ("\t% .3f%12f%12f\n", x[i], y[i], z[i]);

}

}

void diskr_analog(float a, float b, float *x, float *y, float *z, int m, float n)

{

float k=100,*xx,*zz,*yy;

float sum=0,max=0,p;

xx = (float*)calloc(k+1,sizeof(float));

yy = (float*)calloc(k+1,sizeof(float));

zz = (float*)calloc(k+1,sizeof(float));

float h=(b-a)/k;

for (int i=0; i<=k; i++)

xx[i] = -1+i*h;

for (i=0;i<=k;i++)

yy[i] = f(xx[i]);

for (i=0; i<=k; i++)

zz[i] = g(xx[i],x,n);

for(i=0;i<=k;i++)

{

p=yy[i]-zz[i];

if(fabs(p)>max) max=fabs(p);

sum+=pow(p,2);

}

if(m==1) printf("\nДискретный аналог: р1=%f",max);

else printf("\nДискретный аналог: р2=%f",pow(sum/(k+1),0.5));

}

void main (void)

{

clrscr ();

float n, *x, *y, *z;

printf("Введите количество шагов: ");

scanf("%f",&n);

// динамически создаем массивы из n+1 элементов

x = (float*)calloc((n+1),sizeof(float));

y = (float*)calloc((n+1),sizeof(float));

z = (float*)calloc((n+1),sizeof(float));

//Отрезок интерполяции

float a=-1, b=1;

printf ("Интерполяционная таблица (n=%2.0f)\n",n);

xyz (n, x, y, z, a, b);

diskr_analog(a,b,x,y,z,1,n);

diskr_analog(a,b,x,y,z,2,n);

getch ();

// освобождаем память, выделенную под массивы

clrscr();

int graphdriver= DETECT, graphmode, nn=100;

float x1,y1;

// Инициализация графического режима:

initgraph(&graphdriver,&graphmode,"C:\\BORLANDC\\BGI");

// Запрос параметров:

gotoxy(40,20);

printf(" Enter please parameter n ");

scanf("%d",&nn);

gotoxy(40,21);

printf(" Enter  xmin  xmax ");

scanf("%f %f",&xmin,&xmax);

gotoxy(40,22);

printf(" Enter  ymin  ymax ");

scanf("%f %f",&ymin,&ymax);

// Очистка области запросов

gotoxy(40,20);

printf("                                    ");

gotoxy(40,21);

printf("                                    ");

gotoxy(40,22) ;

printf("                                    ");

xdens=(xmax-xmin)/getmaxx(); //Вычисление коэффициента масштабирования по x

ydens=(ymax-ymin)/getmaxy(); //Вычисление коэффициента масштабирования по y

hx=(xmax-xmin)/nn;                                      // Вычисление шага

setcolor(7);                                          // Установка цвета для вывода осей

line(ex(xmin,0), ey(xmin,0), ex(xmax,0), ey(xmax,0));       // Вывод оси X

line(ex(0,ymax), ey(0,ymax), ex(0,ymin), ey(0,ymin));       // Вывод оси Y

gotoxy(39,2); printf("Y");                  // Вывод подписи оси Y

gotoxy(78,16); printf("X");                // Вывод подписи оси X

gotoxy(39,16); printf("0");                 // Вывод 0 в начале координат

// Вывод стрелок

line(ex(0,ymax),ey(0,ymax),ex(0,ymax)-3,ey(0,ymax)+8);

line(ex(0,ymax),ey(0,ymax),ex(0,ymax)+3,ey(0,ymax)+8);

line(ex(xmax,0),ey(xmax,0),ex(xmax,0)-8,ey(xmax,0)+3);

line(ex(xmax,0),ey(xmax,0),ex(xmax,0)-8,ey(xmax,0)-3);

setcolor(15);                                        // Установка цвета для графика функции

// Вывод графика функции x*sin(x)

for(x1=xmin;x1<xmax;x1+=hx)

line(ex(x1,f(x1)),ey(x1,f(x1)), ex(x1+hx, f(x1+hx)), ey(x1+hx, f(x1+hx)));

for(x1=xmin;x1<xmax;x1+=hx)

{setcolor(RED);

line(ex(x1,g(x1,x,n)),ey(x1,g(x1,x,n)), ex(x1+hx,g(x1+hx,x,n)), ey(x1+hx,g(x1+hx,x,n)));

}

getch();             // Ожидание нажатия любой клавиши

closegraph ();   // Выход из графического режима

delete x; delete y; delete z;

}

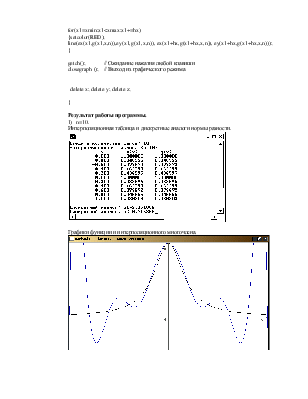
Результат работы программы.

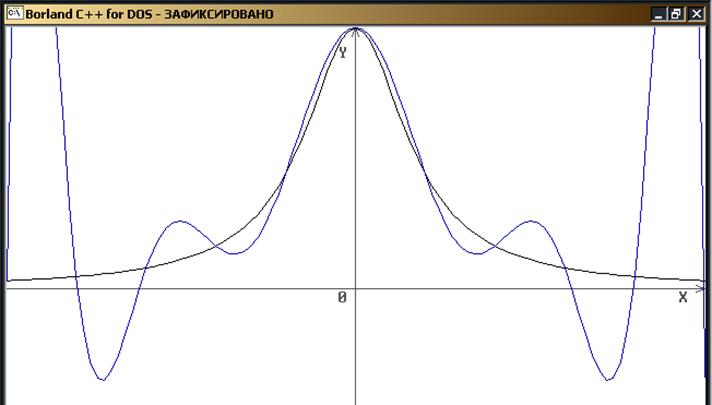
1)  n=10.

Интерполяционная таблица и дискретные аналоги нормы разности.

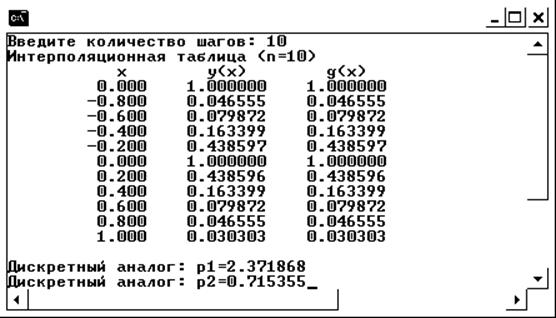
Графики функции и интерполяционного многочлена.

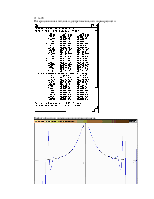
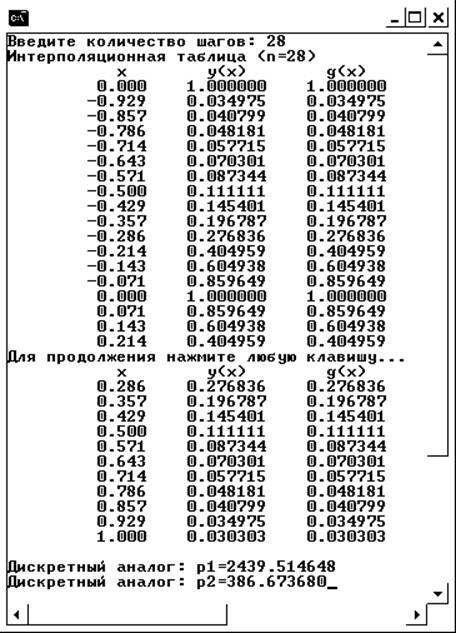
2)  n=28

Интерполяционная таблица и дискретные аналоги нормы разности.

Графики функции интерполяционного многочлена.

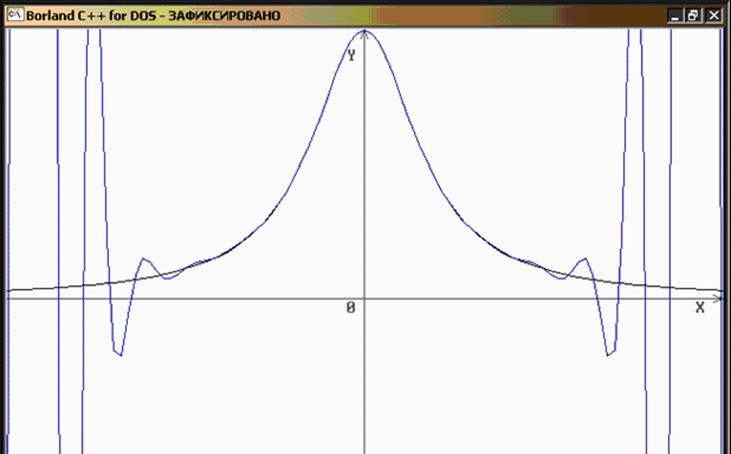
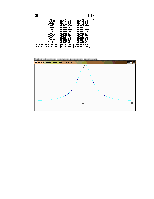
2. Узлы интерполяции совпадают с нулями полинома Чебышева.

Вычисление узлов интерполяции:

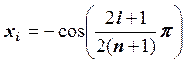,  0 £ i £ n,    где x_i – нули полинома Чебышева степени n + 1.

Построение интерполяционной таблицы: (x_i,y_i), , y_i=f(x_i)

Построение интерполяционного полинома Лагранжа по соответствующей формуле.

Вычисление дискретных аналогов нормы разности интерполяционного полинома и функции по соответствующей формулам.

Листинг программы.

// Подключаемые библиотеки

#include <conio.h>

#include <stdio.h>

#include <math.h>

#include<stdlib.h>

#include <graphics.h>

float xmin, xmax;                  // Область изменения x

float ymin, ymax;                  // Область изменения y

float hx;                          // Шаг

float xdens, ydens;

// Вычисление экранной x координаты

int ex(float x,float y)

{return (int) ((x-xmin)/xdens);}

// Вычисление экранной y координаты

int ey(float x,float y)

{return (int) ((ymax-y)/ydens);}

// функция возвращает значение заданной функции

float f (float x) { return 1/(1+32*x*x); }

// функция возвращает значение интерполяционного полинома в форме Лагранжа

float g (float X, float *x, float n)

{

double p,s=0;

for (int i=0; i<=n; i++)

{

p = 1;

for (int j=0; j<=n; j++)

{

if (i==j) continue;

p *= (X-x[j])/(x[i]-x[j]);

}

s += p*f(x[i]);

}

return s;

}

// Построение по формуле функции f(x) интерполяционной таблицы размер// ности n+1(узлы интерполяции совпадают с нулями полинома Чебышева)

// Массив x - узлы интерполяции (нули полинома Чебышева),

// Массив y - значения функции f(x) в узлах сетки.

// Массив z - значения интерполяционного полинома

void xyz (float n, float *x, float *y, float *z)

{

for (int i=0; i<=n; i++)

{

x[i] = -cos(3.14159*(2*i+1)/(2*(n+1)));

y[i] = f(x[i]);

}

for (i=0; i<=n; i++) z[i] = g(x[i],x,n);

printf ("\t   x        y(x)        g(x)\n");

for (i=0; i<=n; i++)

{

if (i==18)  // при заполнении страницы ждем нажатия клавиши

{

printf ("Для продолжения нажмите любую клавишу...\n");

getch ();

printf ("\t   x        y(x)        g(x)\n");

}

printf ("\t% .3f%12f%12f\n", x[i], y[i], z[i]);

}

}

void diskr_analog(float *x, float *y, float *z, int m, float n)

{

float k=100,*xx,*yy,*zz;

double sum=0,max=0,p;

xx = (float*)calloc(k+1,sizeof(float));

yy = (float*)calloc(k+1,sizeof(float));

zz = (float*)calloc(k+1,sizeof(float));

float h=2.0/k;

for (int i=0; i<=k; i++)

{

xx[i] = -1+i*h;

yy[i] = f(xx[i]);

}

for (i=0; i<=k; i++) zz[i] = g(xx[i],x,n);

for (i=0;i<=k;i++)

{

p=yy[i]-zz[i];

if(fabs(p)>max) max=fabs(p);

sum+=(p*p);

}

if(m==1) printf("Дискретный аналог разности p1=%lf", max);

else printf("\nДискретный аналог разности p2=%lf",pow(sum/(k+1),0.5));

}

void main (void)

{

clrscr ();

float n, *x, *y, *z;

printf("Введите количество шагов: ");

scanf("%f",&n);

// динамически создаем массивы из n+1 элементов

x = (float*)calloc((n+1),sizeof(float));

y = (float*)calloc((n+1),sizeof(float));

z = (float*)calloc((n+1),sizeof(float));

printf ("Интерполяционная таблица (n=%2.0f)\n",n);

xyz (n, x, y, z);

diskr_analog(x,y,z,1,n);

diskr_analog(x,y,z,2,n);

getch ();

clrscr();

int graphdriver= DETECT, graphmode, nn=100;

float x1,y1;

// Инициализация графического режима:

initgraph(&graphdriver,&graphmode,"C:\\BORLANDC\\BGI");

// Запрос параметров:

gotoxy(40,20);

printf(" Enter please parameter n ");

scanf("%d",&nn);

gotoxy(40,21);

printf(" Enter  xmin  xmax ");

scanf("%f %f",&xmin,&xmax);

gotoxy(40,22);

printf(" Enter  ymin  ymax ");

scanf("%f %f",&ymin,&ymax);

// Очистка области запросов

gotoxy(40,20);

printf("                                    ");

gotoxy(40,21);

printf("                                    ");

gotoxy(40,22) ;

printf("                                    ");

xdens=(xmax-xmin)/getmaxx(); //Вычисление коэффициента масштабирования