Интерполяция функции интерполяционным многочленом Ньютона для интерполирования вперед

Министерство образования и науки РФ

ГОУВПО «Комсомольский-на-Амуре государственный технический университет»

Кафедра МОП ЭВМ

Отчет №3

По дисциплине «Ознакомительная практика»

Выполнил: Сюй Н.А.

Группа: 4ВС-1

Проверил: Могильников Е.В.

Комсомольск-на-Амуре

2005

Вариант 9.

Постановка задачи.

Задана функция  своим аналитическим выражением на интервале. Провести интерполяцию этой функции интерполяционным многочленом Ньютона для интерполирования вперед. Оценить погрешность интерполяции. Графически провести сравнение между заданной функцией и интерполяционным многочленом.

Заданная функция:

f(x) = 3 ^-x +5x +1,  n = 22, [-2.8; -3.5]

Алгоритм решения.

1.  Перед программами располагаются общие для них данные: границы интервала, количество разбиений и шаг изменения переменной.

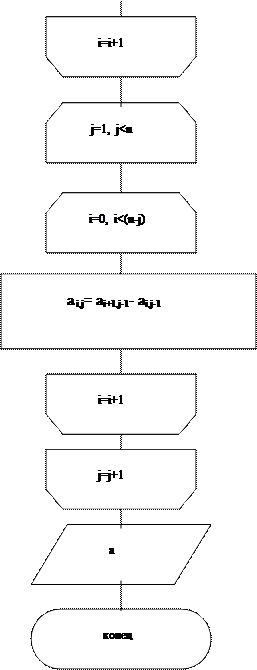
2.  Разработка программы для вычисления конечных разностей. Данная программа не содержит аргументов. Программа возвращает матрицу значений конечных разностей. Для построения матрицы сначала в отдельном цикле вычисляются значения функции в определенных точках, составляющие элементы первого столбца матрицы, затем исходя из того, что конечная разность к-ого порядка вычисляется по формуле: у^к_к+1/2=y^k-1_(k+1)+3/2- y^k-1_(k+1)+1/2 , вычисляем разности до 22-ого порядка включительно.

3.  Написание программы для составления интерполяционного многочлена Ньютона для интерполирования вперед. В качестве аргумента данной программы выступает переменная х, по которой впоследствии будет строиться график. Многочлен вычисляется по формуле: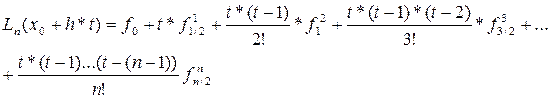

где  .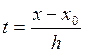

4.  Написание программы для определения погрешности интерполяции.

Чтобы вычислить максимальное значение погрешности, мы находим,  в какой точке на интервале [-2.8,-3.5] n+1 производная получит максимальное значение. Для этого мы находим n+2 производную, она имеет вид: 3^-x*ln(3)²⁴, из неё мы видим, что график функции n+1 производной возрастает. Находим значения n+1 производной по модулю в точках -2,8 и -3,5. Значение в точке -2.8 равно -188.522, а в точке -3.5 равно -406.768. Получаем, что в точке -2.8 n+1 производная получает наибольшее значение на интервале [-2.8,-3.5].  Погрешность вычисляется по  формуле:

.

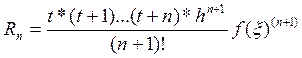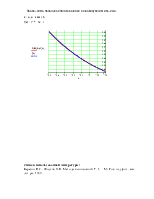
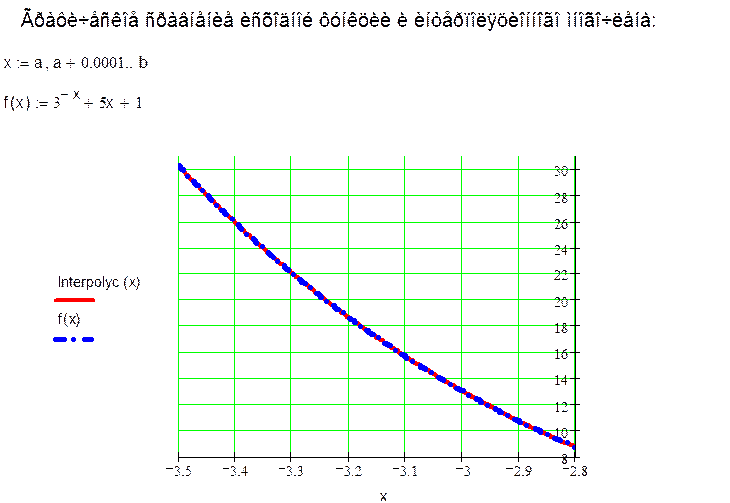
5.  Построение графика заданной функции и  графика интерполяционного многочлена для их сравнения.

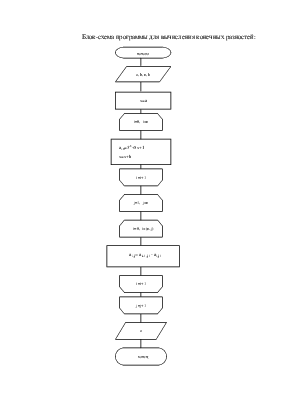
Блок-схема программы для вычисления конечных разностей:

		ai,0=3-x+5x+1 x=x+h

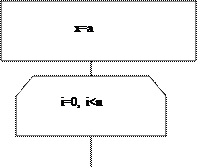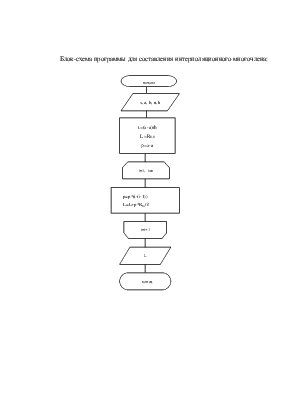
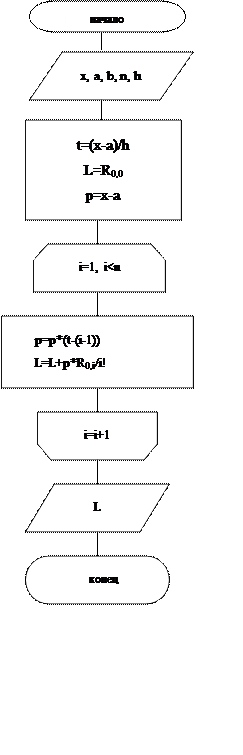
Блок-схема программы для составления интерполяционного многочлена:

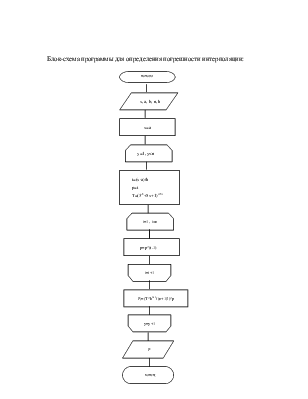
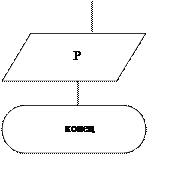
Блок-схема программы для определения погрешности интерполяции:

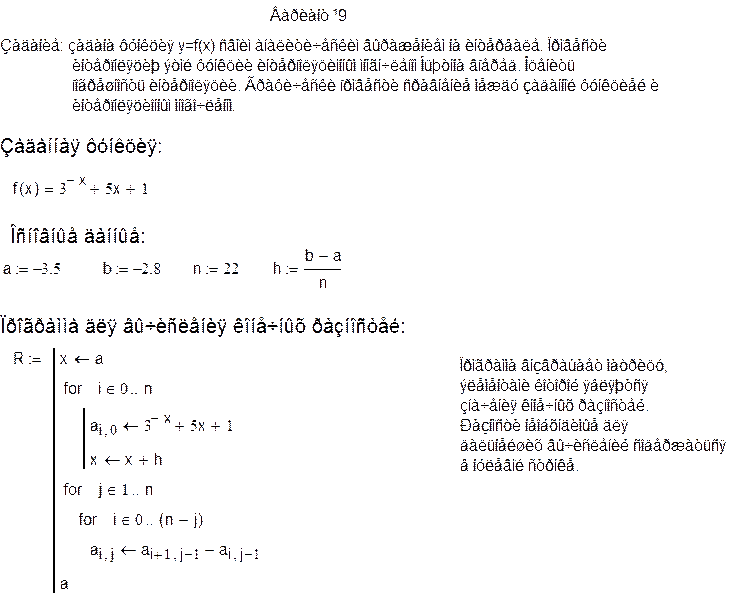
Листинг программы:

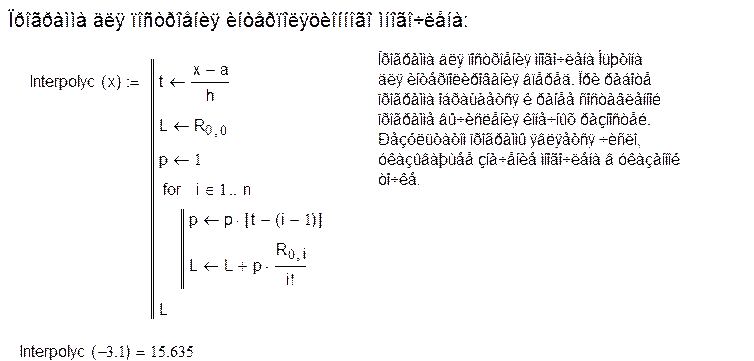
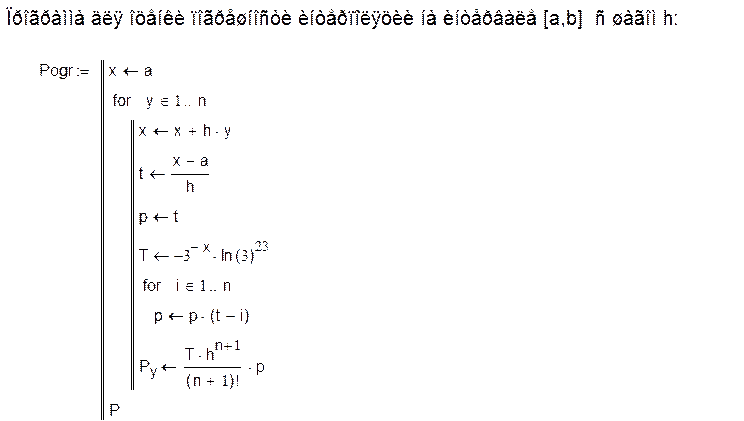
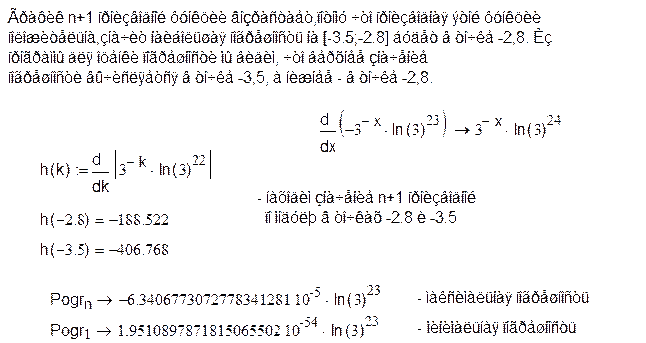
Список использованной литературы:

Березин И.С., Жидков Н.П. Методы вычислений. Т. 1. – М.: Гос. изд. физ.-мат. лит-ры, 1959.