














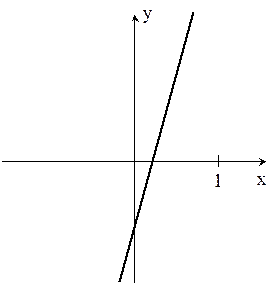 Задание. Отделить корни уравнения
Задание. Отделить корни уравнения ![]() графически и построить алгоритм для
уточнения одного из них методом Ньютона с точностью
графически и построить алгоритм для
уточнения одного из них методом Ньютона с точностью ![]() .
Разработать программу, которая реализует этот алгоритм и выдает на печать
приближенное значение корня и значение функции f(x) в этой точке.
.
Разработать программу, которая реализует этот алгоритм и выдает на печать
приближенное значение корня и значение функции f(x) в этой точке.
Решение
Отделение корней
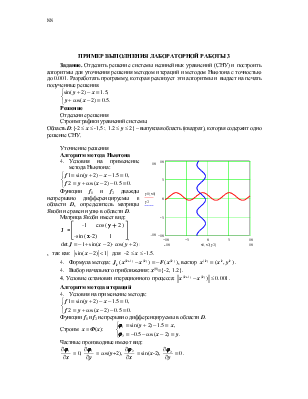
Построим график функции:
![]() .
.
Отрезок [0, 0.9] содержит один корень уравнения.
Уточнение корня
1. Проверка условий на функцию:
![]() .
.
Функция f(x) дважды непрерывно дифференцируема на отрезке [0, 0.9], на концах отрезка принимает значения разных знаков, первая и вторая производные функции f(x) не обращаются в ноль на этом отрезке:
![]() ;
; ![]() ,
, ![]() ,
,
![]() и
и ![]() на
отрезке [0, 0.9].
на
отрезке [0, 0.9].
2. Формула метода: ![]() .
.
3. Выбор начального приближения: ![]() ,
,
![]() .
.
4. Условие остановки итерационного процесса:
![]() , где
, где ![]() .
.
Программа
// Подключаемые библиотеки
#include <math.h>
#include <conio.h>
#include <stdio.h>
// Прототипы функций
float f(float x) // Заданная функция
{ return (x*x*x-3*x*x+6*x-1); }
float fpro(float x) //Производная функции
{ return (3*x*x-6*x+6);}![]()
void main(void)
{
// eps – заданная точность метода;
// m – заранее вычисленное число m;
// x0 – начальная точка;
// x_current – текущее приближение корня (x[n]);
// x_next – следующее приближение корня (x[n+1]).
float eps=0.001, m=3.03;
float x0=0, x_current, x_next;
x_current=x0;
do
{
// Формуламетода
x_next=x_current-f(x_current)/fpro(x_current);
x_current=x_next;
}
// Проверка на выполнение условия остановки
while(fabs(f(x_next))>=m*eps);
clrscr(); //очищение экрана
printf("\n\n\tПриближенное значение корня: x=%.3f",x_next);
printf("\n\tЗначение функции в этой точке: f(x)=%.3f",f(x_next));
getch();
}
Результат работы программы
Приближенное значение корня: x=0.182
Значение функции в этой точке: f(x)=-0.001
Задание. Построить алгоритм решения системы линейных уравнений методом Гаусса с частичным выбором ведущего элемента:
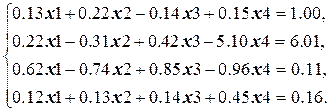
Решение
Прямой ход
На каждом шаге i, 1 £ i £ n-1 сначала находим максимальный по модулю элемент в непреобразованном столбце. Этот элемент является ведущим. Если он равен нулю, то матрица вырожденная. Если максимальный элемент является диагональным, то применяем формулы метода Гаусса, в противном случае сначала переставляем уравнения таким образом, чтобы ведущий элемент оказался на главной диагонали.
Формулы метода Гаусса:
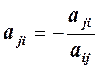 , j = i+1, i+2, … n,
, j = i+1, i+2, … n,
![]() , k = i+1, i+2, … n,
, k = i+1, i+2, … n,
![]() ,
,
![]() .
.
Обратная подстановка
Находим неизвестные в обратном порядке:
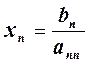 , i = 1, 2, … n-1,
, i = 1, 2, … n-1,
m = n – i,
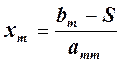 ,
где
,
где 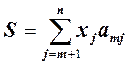 .
.
Программа
// Подключаемые библиотеки
#include <iostream.h>
#include <math.h>
#include <conio.h>
void main()
{
clrscr();
int i,j; // счетчикициклов
float A[4][4],B[4],As[4][4],Bs[4];
// исходнаяматрица
A[0][0]=0.13; A[0][1]=0.22; A[0][2]=-0.14; A[0][3]=0.15;
A[1][0]=0.22; A[1][1]=-0.31; A[1][2]=0.42; A[1][3]=-5.01;
A[2][0]=0.62; A[2][1]=-0.74; A[2][2]=0.85; A[2][3]=-0.96;
A[3][0]=0.12; A[3][1]=0.13; A[3][2]=0.14; A[3][3]=0.45;
// исходный вектор
B[0]=1; B[1]=6.01; B[2]=0.11; B[3]=0.16;
float x[4]; // вектор решений
float R[4]; // вектор невязки
float B_[4];// вспомогательный вектор
// Cохранение матрицы
for (i=0;i<4;i++)
{
Bs[i]=B[i];
for (j=0;j<4;j++) { As[i][j]=A[i][j]; };
};
//Решение системы уравнений
//k-счетчик циклов
//numb-номер строки с ведущим элементом
//max-максимальный по модулю элемент непреобразованного столбца
//str,bstr- используются при перестановке строк
//L-коэффициент преобразования
int numb=0, k;
float max, str, bstr, L;
// Приведение матрицы к U-виду
for (j=0;j<3;j++)
{
max=fabs(A[j][j]);
numb=j;
// Определение максимального элемента в столбце
for (i=j;i<4;i++)
{
if (max<fabs(A[i][j]))
{ max=fabs(A[i][j]); numb=i; };
};
// если максимум – не диагональный элемент, то…
if (numb!=j)
{
//…замена строк
for (i=0;i<4;i++)
{
str=A[numb][i];
A[numb][i]=A[j][i];
A[j][i]=str;
};
bstr=B[numb];
B[numb]=B[j];
B[j]=bstr;
};
// преобразование столбца
for (i=j+1;i<4;i++)
{
L=-(A[i][j]/A[j][j]); // вычисление коэффициента
A[i][j]=0.0;
// обнуление элемента текущего столбца
for (k=j+1;k<4;k++) { A[i][k]=A[i][k]+A[j][k]*L; };
// и вычисление последующих в строке
B[i]=B[i]+B[j]*L;
};
};
// Решение системы линейных уравнений
for (j=3;j>=0;j--)
{
x[j]=B[j]/A[j][j];
if (j!=3)
{
for (i=3;i>j;i--) {x[j]=x[j]-A[j][i]*x[i]/A[j][j];};
};
};
//Вычисление вектора невязки
//предварительно восстанавливаем исходные значения матрицы и вектора
for (i=0;i<4;i++)
{
B[i]=Bs[i];
for (j=0;j<4;j++) { A[i][j]=As[i][j]; };
};
for (i=0;i<4;i++)
{
B_[i]=0;
//вычисление элементов вспомогательного вектора
for (j=0;j<4;j++) { B_[i]=B_[i]+A[i][j]*x[j]; };
R[i]=B[i]-B_[i];
};
//Вывод значений
cout<<»\n\tРешение систем линейных уравнений.»;
cout << «\n\n» << «Решение СЛУ:» << «\n»;
for (i=0;i<4;i++) { cout <<x[i] << “\n”; };
cout << «\n»;
cout << «Вектор невязки:» << «\n»;
for (i=0;i<4;i++) { cout << R[i] << “\n”; };
getch();
}
Результат работы программы
Решение систем линейных уравнений.
Решение СЛУ:
2.836329
3.557081
-0.33739
-1.323434
Вектор невязки:
0
-4.768372e-07
-1.117587e-07
5.960464e-08
Задание. Отделить решение системы нелинейных уравнений (СНУ) и построить алгоритмы для уточнения решения методом итераций и методом Ньютона с точностью до 0.001. Разработать программу, которая реализует эти алгоритмы и выдает на печать полученные решения.
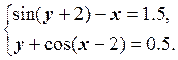
Решение
Отделение решения
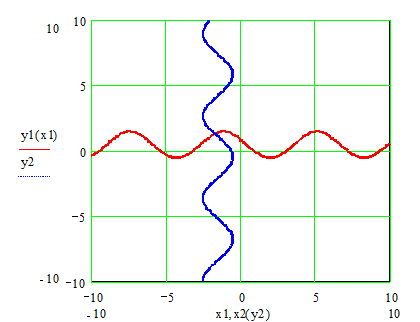
Строим графики уравнений системы.
Область D:{-2 £ x £ -1,5 ; 1.2 £ y £ 2} – выпуклая область (квадрат), которая содержит одно решение СНУ.
Уточнение решения
 Алгоритм метода Ньютона
Алгоритм метода Ньютона
4. Условия на применение метода Ньютона:
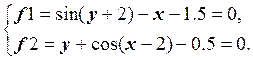
Функции f1 и f2 дважды непрерывно дифференцируемы в области D, определитель матрицы Якоби не равен нулю в области D.
Матрица Якоби имеет вид:
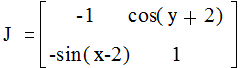 ,
,
![]() , так как
, так как ![]() | для –2 £ x £ -1.5.
| для –2 £ x £ -1.5.
4. Формула
метода: ![]() , вектор
, вектор ![]() .
.
4. Выбор начального приближения: х(0)={-2, 1.2}.
4. Условие остановки итерационного процесса: ![]() .
.
Алгоритм метода итераций
4. Условия на применение метода:
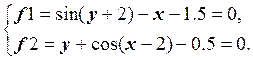
Функции f1 и f2 непрерывно дифференцируемы в области D.
Строим x = Ф(x): 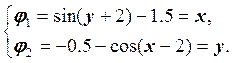
Частные производные имеют вид:
![]() = 0,
= 0, ![]() = cos(y+2),
= cos(y+2), ![]() = sin(x-2),
= sin(x-2), 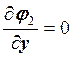 .
.
Тогда матрица М имеет вид:
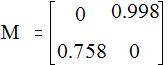 ,
,
|| M || = 0.998 < 1.
2. Формула метода: ![]() , вектор
, вектор
![]() .
.
4. Выбор начального приближения: х0 = {-2, 1.2}.
4. Условие остановки: ![]() (1-||M||)/||M||.
(1-||M||)/||M||.
Метод Ньютона
Программа
#include <math.h>
#include <conio.h>
#include <iostream.h>
#include <stdio.h>
void main()
{
float eps=0.001; // точность вычислений
int i, j; // счётчикициклов
float xb[2]={-2, 1.2}; // вектор начального приближения
float B[2],x[2]; //B-вектор системы, x=xb(след.)-xb(тек.)
float A[2][2]; // матрица Якоби
float nx; //норма вектора x
do
{
// Вычисляем значение свободного вектора от текущих значений x и y
B[0]=-sin(xb[1]+2)+xb[0]+1.5;
B[1]=-xb[1]-cos(xb[0]-2)+0.5;
//Вычисляем значение матрицы Якоби от текущих значений
A[0][0]=-1; // df1/dx
A[0][1]=cos(xb[1]+2); // df1/dy
A[1][0]=-sin(xb[0]-2); // df2/dx
A[1][1]=1; // df2/dy
// Вычисляем вектор х по методу Гаусса с ЧВВЭ
// k-счетчик циклов
// numb-номер строки с ведущим элементом
// max-максимальный по модулю элемент непреобразованного столбца
// str,bstr – используются при перестановке строк
// L-коэффициент преобразования
int numb=0, k;
float max, str, bstr, L;
// Приведение матрицы к U-виду
for (j=0;j<1;j++)
{
max=fabs(A[j][j]);
numb=j;
// Определение максимального элемента в столбце
for (i=j;i<2;i++)
{
if (max<fabs(A[i][j]))
{ max=fabs(A[i][j]); numb=i; };
};
// Если максимум – не диагональный элемент, то...
if (numb!=j)
{
//...замена строк
for (i=0;i<2;i++)
{
str=A[numb][i];
A[numb][i]=A[j][i];
A[j][i]=str;
};
bstr=B[numb];
B[numb]=B[j];
B[j]=bstr;
};
// Преобразование столбца
for (i=j+1;i<2;i++)
{
L=-A[i][j]/A[j][j]; // вычисление коэффициента
// Обнуление элемента текущего столбца
// и вычисление последующих в строке
for (k=j+1;k<2;k++) A[i][k]=A[i][k]+A[j][k]*L;
B[i]=B[i]+B[j]*L;
};
};
// Решение системы линейных уравнений
for (j=1;j>=0;j--)
{
x[j]=B[j]/A[j][j];
if (j!=1) for (i=1;i>j;i--) x[j]=x[j]-A[j][i]*x[i]/A[j][j];
};
// Расчет первой нормы вектора х
nx=fabs(x[0]);
for (i=1;i<2;i++) if (nx<fabs(x[i])) nx=fabs(x[i]);
//Расчет вектора решений
for (i=0;i<2;i++) xb[i]=x[i]+xb[i];
}
while (nx>eps); // если условие остановки не выполняется, то
// вектор решения становится текущим вектором
// Вывод результата
clrscr();
cout << "\tРешение СНУ по методу Ньютона:\n";
for (i=0;i<2;i++) printf("\t%.4f\n",xb[i]);
getch();
}
Результат работы программы
Решение СНУ по методу Ньютона:
-1.7033
1.3463
Метод итераций
Программа
#include <math.h>
#include <conio.h>
#include <iostream.h>
#include <stdio.h>
void main()
{
float eps=0.001; //заданная точность
int i, j; //счётчикициклов
float nM=0.998, nraznost; //nM – нормаматрицыМ
//nraznost – норма вектора
float x[2]={-2, 1.2}; // начальный вектор
float Fi[2], raznost[2]; //Fi – вектор-функция
//raznost=(х(след.)-х(тек.))
do
{
//Расчёт вектор-функции от текущих значений х и у
Fi[0]=sin(x[1]+2)-1.5;
Fi[1]=-cos(x[0]-2)+0.5;
//Расчетвектораразности
for (i=0;i<2;i++) raznost[i]=Fi[i]-x[i];
//Расчет нормы вектора разности для проверки условия остановки
nraznost=fabs(raznost[0]);
for (i=1;i<2;i++)
if (nraznost<fabs(raznost[i]))
nraznost=fabs(raznost[i]);
//Инициализация х(след.)
for (i=0;i<2;i++) x[i]=Fi[i];
}
while (nraznost>((1-nM)*eps/nM)); //если не остановка, то
//х(след.) становиться х(тек.)
//Вывод на печать
clrscr();
cout << "\tРешение СНУ по методу итераций\n";
for (i=0;i<2;i++) printf("\t%.4f\n",x[i]);
getch();
}
Результат работы программы
Решение СНУ по методу итераций
-1.7033
1.3463
Задание. Пусть 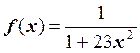 , n=27.
, n=27.
Построить алгоритм для интерполяции f(x) полиномом Лагранжа с неравномерным шагом так, чтобы узлы интерполяции совпали с нулями полинома Чебышева степени n + 1.
Решение
Сначала найдем узлы интерполяции:
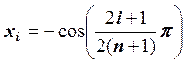 , 0 £ i £ n, где xi – нули полинома Чебышева
степени n + 1.
, 0 £ i £ n, где xi – нули полинома Чебышева
степени n + 1.
Построим интерполяционную таблицу: (xi , yi ), 0 £ i £ n, yi = f(xi).
Запишем алгоритм построения полинома Лагранжа g(x):
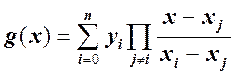 для 0 £ j £ n.
для 0 £ j £ n.
Программа
// Подключаемые библиотеки
#include <conio.h>
#include <stdio.h>
#include <math.h>
#include <graphics.h>
// функция возвращает значение заданной функции
float f (float x) { return 1/(1+23*x*x); }
// функция возвращает значение интерполяционного полинома в форме Лагранжа
float g (float X, float *x, float n)
{
double p,s=0;
for (int i=0; i<=n; i++)
{
p = 1;
for (int j=0; j<=n; j++)
{
if (i==j) continue;
p *= (X-x[j])/(x[i]-x[j]);
}
s += p*f(x[i]);
}
return s;
}
// Построение по формуле функции f(x) интерполяционной таблицы размер-
// ности n+1(узлы интерполяции совпадают с нулями полинома Чебышева)
// Массив x – узлы интерполяции (нули полинома Чебышева),
// Массив y – значения функции f(x) в узлах сетки.
// Массив z – значения интерполяционного полинома
void xyz (float n, float *x, float *y, float *z)
{
for (int i=0; i<=n; i++)
{
x[i] = -cos(3.14159*(2*i+1)/(2*(n+1)));
y[i] = f(x[i]);
}
for (i=0; i<=n; i++) z[i] = g(x[i],x,n);
printf ("\t x y(x) g(x)\n");
for (i=0; i<=n; i++)
{
if (i==18) // при заполнении страницы ждем нажатия клавиши
{
printf ("Для продолжения нажмите любую клавишу...\n");
getch ();
printf ("\t x y(x) g(x)\n");
}
printf ("\t% .3f%12f%12f\n", x[i], y[i], z[i]);
}
}
void main (void)
{
clrscr ();
float n = 27, *x, *y, *z;
// динамически создаем массивы из n+1 элементов
x = new float[n+1];
y = new float[n+1];
z = new float[n+1];
printf ("Интерполяционная таблица (n=27)\n");
xyz (n, x, y, z);
printf ("\nЗначение функции при x = 0.1: %f", f(0.1));
printf ("\nЗначение интерполяционного полинома при x =0.1:
%f",g(0.1, x, n));
getch ();
// освобождаем память, выделенную под массивы
delete x; delete y; delete z;
}
Результат работы программы
Интерполяционная таблица (n=27)
x y(x) g(x)
-0.998 0.041793 0.041793
-0.986 0.042818 0.042818
-0.961 0.044969 0.044969
-0.924 0.048469 0.048469
-0.875 0.053710 0.053710
-0.816 0.061356 0.061356
-0.746 0.072529 0.072529
-0.666 0.089187 0.089187
-0.579 0.114919 0.114919
-0.484 0.156699 0.156699
-0.383 0.228923 0.228923
-0.277 0.361967 0.361967
-0.168 0.607773 0.607773
-0.056 0.932564 0.932564
0.056 0.932570 0.932570
0.168 0.607781 0.607781
0.277 0.361971 0.361971
0.383 0.228925 0.228925
Для продолжения нажмите любую клавишу...
x y(x) g(x)
0.484 0.156701 0.156701
0.579 0.114919 0.114919
0.666 0.089187 0.089187
0.746 0.072529 0.072529
0.816 0.061357 0.061357
0.875 0.053711 0.053711
0.924 0.048469 0.048469
0.961 0.044969 0.044969
0.986 0.042818 0.042818
0.998 0.041793 0.041793
Значение функции при x = 0.1: 0.813008
Значение интерполяционного полинома при x = 0.1: 0.817669
Задание.
Построить алгоритм для вычисления приближенного значения интеграла 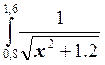 по формуле Симпсона при n = 8 иn = 16, гдеn–
это число интервалов, и оценить погрешность по правилу Рунге.
по формуле Симпсона при n = 8 иn = 16, гдеn–
это число интервалов, и оценить погрешность по правилу Рунге.
Решение
Формулу Симпсона (составную квадратичную формулу Симпсона) можно применять при четных n. В нашем случае n четно.
a = 0.8, b = 1.6, h1 = (b – a) / n1, n1 = 8,
m1 = n1 / 2 = 4,
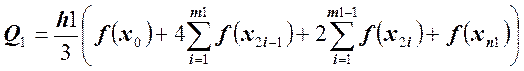 ,
,
![]() , 0 £ i
£ n1, x0 = a.
, 0 £ i
£ n1, x0 = a.
Q1 – приближенное значение интеграла при n = 8.
h2 = (b – a) / n2 , n2 = 16, m2 =n2 / 2 = 8,
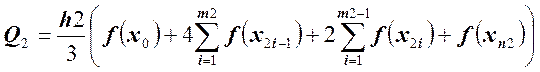 ,
,
![]() , 0 £ i
£ n2, x0 = a.
, 0 £ i
£ n2, x0 = a.
Q2 – приближенное значение интеграла при n = 16.
Оценка погрешности по правилу Рунге:
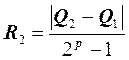 , p = 4,
, p = 4, 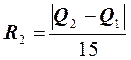 , где R2 – оценка
погрешности, полученная по правилу Рунге.
, где R2 – оценка
погрешности, полученная по правилу Рунге.
Программа
//Подключаемые библиотеки
#include <conio.h>
#include <stdio.h>
#include <math.h>
// Заданнаяфункция
float f1 (float x) { return 1/sqrt(x*x+1.2); }
void main(void)
{
/* a и b -границы отрезка, на котором ищется интеграл
n – число отрезков
h – шаг
Q1 – значение интеграла при n=8
Q2 – значение интеграла при n=16
*/
float a,b,h,Q1,Q2,Q; int n,i; // объявили переменные
clrscr(); // очистка экрана
printf("\n\t\t Численное интегрирование функций");
puts("\n\n\t*** Формула Симпсона ***");
a = 0.8; b = 1.6;
n = 8; h = (b-a)/n;
Q1 = f1(a)+f1(b);
float s1=0, s2=0, x=a;
for (i=1; i<n; i++)
{
x += h;
if (i%2)
// сумма значений функции в точках с нечетными номерами
s1 += f1(x);
else
// сумма значений функции в точках с четными номерами
s2 += f1(x);
}
Q1 = h/3*(Q1+4*s1+2*s2);
printf ("\n\t\tn= 8:");
printf ("\n Приближенное значение интеграла: %.7f", Q1);
n = 16;
h = (b-a)/n;
Q2 = f1(a)+f1(b);
s1=0; s2=0; x=a;
for ( i=1; i<n; i++)
{
x += h;
if (i%2)
// сумма значений функции в точках с нечетными номерами
s1 += f1(x);
else
// сумма значений функции в точках с четными номерами
s2 += f1(x);
}
Q2 = h/3*(Q2+4*s1+2*s2);
printf ("\n\t\tn= 16:");
printf ("\n Приближенное значение интеграла: %.7f", Q2);
Q= fabs(Q1-Q2)/15;
printf("\n\n Оценка погрешности по правилу Рунге: R=%.2e",Q);
getch();
}
Численное интегрирование функций
*** Формула Симпсона ***
n= 8:
Приближенное значение интеграла: 0.4953933
n= 16:
Приближенное значение интеграла: 0.4953938
Оценка погрешности по правилу Рунге: R=2.98e-08
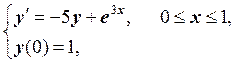
с шагом h = 0.1методом Рунге-Кутта четвертого порядка.
Решение
Запишем задачу Коши в виде:
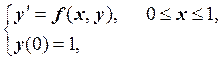
где ![]() .
Известно, что задача Коши имеет единственное решение, если |
.
Известно, что задача Коши имеет единственное решение, если |![]() | £ M, M >
0. В нашем случае
| £ M, M >
0. В нашем случае ![]() = – 5, M = 5. Условие выполнено, следовательно, задача Коши
имеет единственное решение.
= – 5, M = 5. Условие выполнено, следовательно, задача Коши
имеет единственное решение.
Запишем алгоритм метода Рунге-Кутта четвертого порядка:
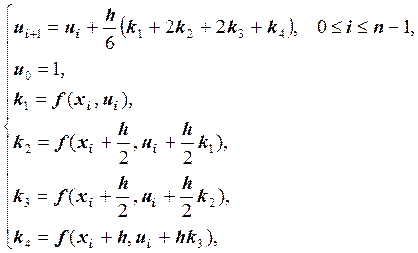
где h = 0.1, n = 1/h
= 10, ![]() xi,
xi,
![]() .
.
Приближенным решением является сеточная функция: u = (u0, u1, u2, … u10).
Программа
//Подключаемые библиотеки
#include <conio.h>
#include <math.h>
#include <stdio.h>
/* Глобальные переменные и массивы:
n – число узлов сетки
x[n] – массив узлов сетки
y[n] – массив значений точного решения
u[n] – массив значений приближенного решения
h – шаг сетки
m,k – параметры, входящие в формулу точного решения
K1,K2,K3,K4 – коэффициенты метода Рунге-Кутта
*/
const int n = 1/0.1+2;
double x[n], y[n], u[n], h = 0.1,
m = 5, k = 3, K1, K2, K3, K4;
// возвращает значение функции (правой части ДУ)
double f (double x,double y) { return -m*y+exp(k*x); }
void main (void)
{
clrscr ();
printf("\n\n численное решение задачи Коши для обыкновенных\n\
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.