Радиотехнические комплексы как большие системы, страница 2

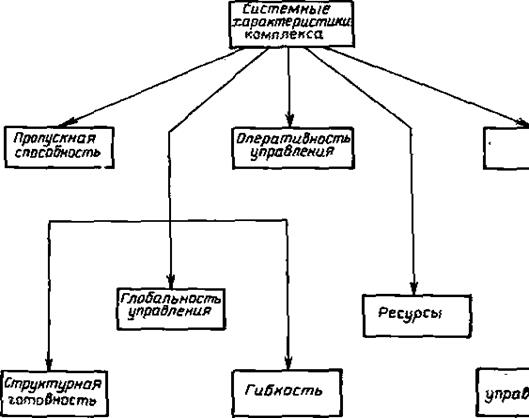
Рис.4.2

Пропускная  способность  характеризует способность комплекса обслуживать с заданным качеством некоторое количество КА. Основными показателями этого свойства обычно являются: среднее количество объектов (по типам), которыми РТКУ способен управлять с заданным качеством в установленном промежутке времени; вероятность проведения  заданного числа сеансов в сутках.

Глобальность управления характеризует способность комплекса вести обмен с КА в некоторых областях пространства.

Оперативность управления характеризует быстроту реакций  принятия решений, а иак же задержка в передаче решений и распоряжений.

Надежность управления характеризует способность комплекса выполнять операции в условиях отказа элементов и связей системы.

Гибкость комплекса  характеризует его приспособляемостью к изменению цели.

Структурная готовность комплекса показывает уровень завершенности структуры РТКУ,

соответствие результата проектирования и модели. Ресурсы на создание и функционирование РТКУ подразделяются на материальные, финансовые, энергетические и людские должны соответствовать времени жизни  КА. Устойчивость -  характеризует способность комплекса сохранять основные показатели в условиях противодействия.

Неуязвимость – возможность противостоять целенаправленным действиям противника. Достигается за счет скрытности, маневренности.

Защищенность – способность противостоять отрицательным воздействиям противника.

Живучесть- обеспечивается за счет функциональной избыточности.

Функциональная эффективность  применения  РТКУ есть динамическое свойство комплекса обеспечивать управление заданной совокупностью КА с требуемым качеством.

Показатели – вероятность выполнения задачи,  либо целевой функции, т.е. совокупности выполнения разнородных задач. На рис. 4.3 показана развернутая структура РТКУ « устойчивость управления». При отсутствии конфликтующей стороны устойчивость управления сводится к надежности, помехоустойчивости и гибкости.

Функциональная эффективность – совокупный критерий качества.

ФЭ есть динамическое свойство комплекса обеспечивать управление с заданным качеством. Требуемое качество задается в виде ограничений  (пределов).  Существует принцип создания равнопрочной системы, в которой обеспечивается одинаковая чувствительность показателя эффективности к изменению параметров.

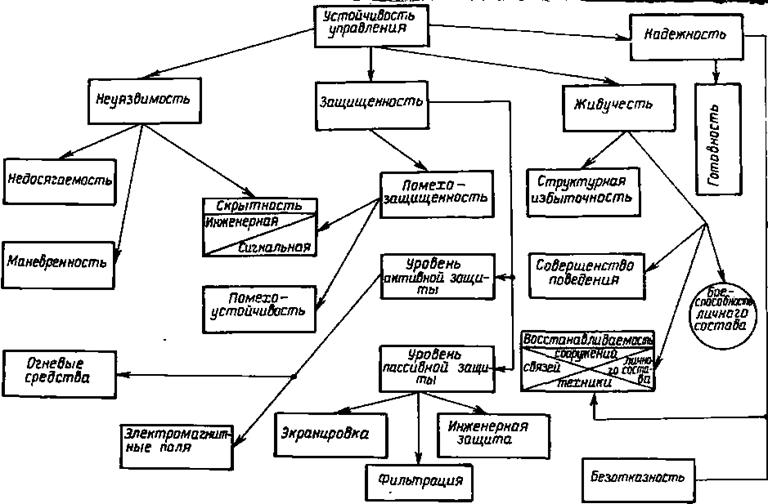
Рис.4.3

Модели космических радиотехнических комплексов

Основное требование, предъявляемое к модели является требование адекватности, рис.4.4

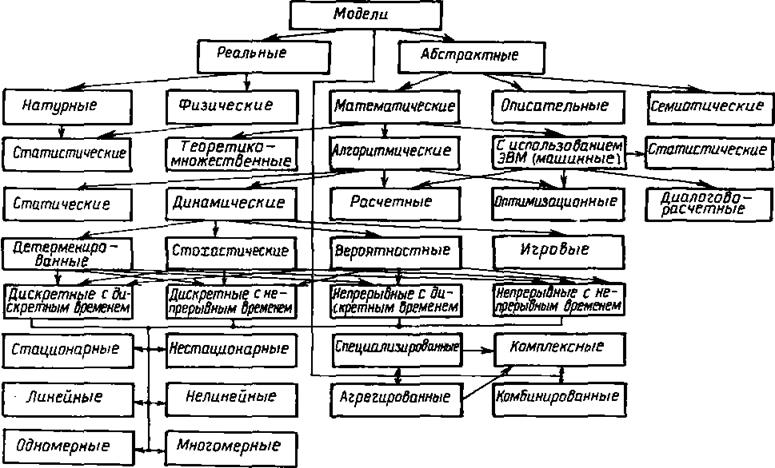
Теоретико – множественная модель. Любой КРТК как некоторая система обладает структурой  ê S  ê и обеспечивает в процессе функционирования Sдостижении цели S,

S=(ê S  ê, S,   S). Являясь открытыми системами КРТК взаимодействуют с другими системами и на них воздействует окружающая среда С=(êС  ê, С,   С) и противника

S_п=(ê Sп  ê, Sп,   Sп).

Воздействие на комплекс проявляется в двойственной форме с одной стороны – воздействие на элементы структуры,  с другой на поведение S. Таким образом  показатель S изменяется во времени – функциональные модели.

Как пример целесообразно рассмотреть функционирование комплекса как систему массового обслуживания. В этом случае наблюдается плавное изменение свойств комплекса, а не разрушение комплекса.  Главное свойство это линейное изменение значений локальных параметров системы. Используются модели типа гибели и размножения. Размножению соответствуют процессы поступлению требований на обслуживание, гибели завершению обслуживания КА. Переход из состояния возможен в два направления.

Вероятность пребывания системы в i-состоянии определяется в результате трех событий

1.В момент времени t РТКУ может находится  в i состоянии и не перейти в соседние состояния i+1,i-1 (первый член).

2. В момент t система находится в состоянии i-1 и переходит в i ( второе слагаемое)

3. . В момент t система находится в состоянии i+1 и переходит в i ( третье слагаемое)

Эти же уравнения могут быть определены для любого состояния i, i=1,N

Это модели с дискретными состояниями.

Рассчитываются возможные переходы. Среднее состояние системы  S

,

Длина очереди на обслуживание  КА. 

Если интенсивности переходов удовлетворяют экспоненциальному закону распределения , функция распределения F(dt)=ldt и уравнение запишется следующим образом:

В матричном виде уравнение выглядит так:

-А матрица интенсивности переходов, сушествует стационарное состояние

Таким образом, удается грубо определить структуру КРТК.