и гранецентрированные решетки Браве. Если узлы кристаллической решетки расположены только в вершинах параллелепипеда, представляющего собой элементарную ячейку,то такая решетка называется примитивной или простой, если, кроме того, имеются узлы в центре оснований параллелепипеда, то решетка называется базоцентрированной, если есть узел в месте пересечения пространственных диагоналей — решетка называется объемноцентрированной, а если имеются узлы в центре всех боковых граней — гранецентрированной.
В 1867 г. русский инженер и кристаллограф А. В. Гадолин показал, что может существовать 32 возможные комбинации элементов симметрии. Каждая из таких возможных комбинаций элементов симметрии называется классом симметрии. В 1881 г. выдающийся русский кристаллограф Е. С. Федоров исследовал все мыслимые пространственные расположения частиц кристалла, исходя из того, что' плотное заполнение пространства кристаллическими ячейками возможно только при определенной форме ячеек, и установил, что внутри 32 классов симметрии может существовать 230 различных пространсгцвенных групп (т.е. 230 типов геометрического расположения атомов в кристаллах). Несколько позже Ё.С.Федорова к такимже результатам пришел немецкий математик А.Шенфлис.
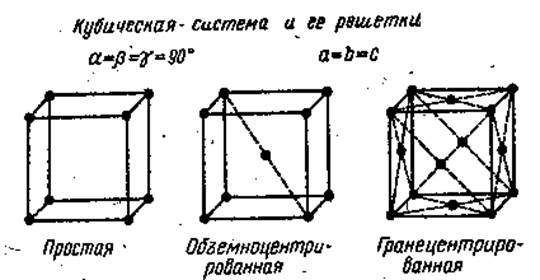
Рис.3
По форме ячейки в зависимости от углов между ее гранями a, b, n (рис.2) и от соотношения между величиной ребер а, b, с различают семь кристаллических систем (сингоний):
1) правильная или кубическая;
2) гексагональная;
3) тетрагональная;
4) тригональная или ромбоэдрическая;
5) ромбическая;
6) моноклинная и
7) триклинная.
В кристаллах кубической системы (см. рис.3) возможны три решетки: простая, объемноцентрированная и гранецентрированная.
В кубической системе все углы элементарной ячейки прямые и все ребра ее равны между собой.
Элементарная ячейка гексагональной системы представляет собой прямую призму, в основании которой лежит ромб с углами 60 и 120° (рис. 1.4). Два угла между осями ячейки прямые, а один равен 120°.
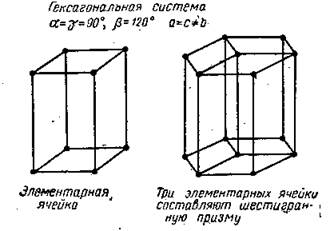
Рис.4
Высота элементарной призмы не равна длине стороны ромба, лежащего в основании. Три таких ячейки составляют гексагональную призму, которая имеет более тесную связь с элементами симметрии, чем примитивная ячейка. Таким образом, элементарная ячейка сингонии не всегда является элементарной ячейкой примитивной решетки.
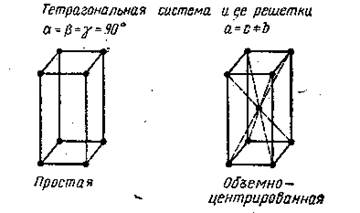
Рис. 5
Простейшая ячейка в тетрагональной системе представляет собой прямоугольный параллелепипед, в основании которого лежит квадрат (рис.5). В этой системе наблюдаются два варианта решетки: простая и объемноцентрированная. Как видно, обе эти решетки отличаются от соответствующих решеток кубической системы только неравенством ребер а и b.
Подробное рассмотрение геометрии других типов кристаллической решетки, см., например, Бушманов Б.Н., и Хромов Ю.А.Физика твердого тела. Учебн. Пособие для втузов. М., “ВШ”
3. 3D решетки Браве
материалы с сайта
http://www.ipm.sci-nnov.ru/~Demidov/Cryst/Cryst_r.html
Решетка Браве - периодическая решетка, состоящая из эквивалентных узлов. Всего в 3D существует 14 различных решеток Браве. Но здесь представлены только 3 типа решеток с кубической симметрией

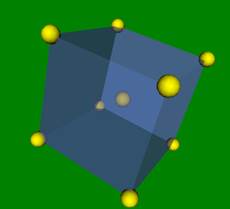
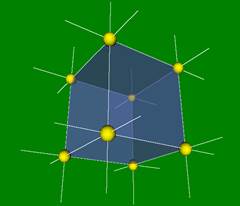 .
.
Простая кубическая элементарная ячейка
Объемо-центрированная кубическая (ОЦК) элементарная ячейка, Такую структуру имеют a-Fe, Na, K, b-Ti.
Гране-центрированная кубическая (ГЦК) элементарная ячейка, Такую структуру имеют Cu, Au, Ag, Al, Pt, Pd.

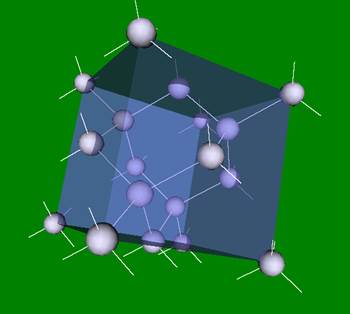
 Si, Ge (и алмаз),
решетка алмаза подобна решетке GaAs, но состоит из атомов одного сорта.
Si, Ge (и алмаз),
решетка алмаза подобна решетке GaAs, но состоит из атомов одного сорта.
 Решетка Si, Ge 5x5x5,
Решетка Si, Ge 5x5x5,
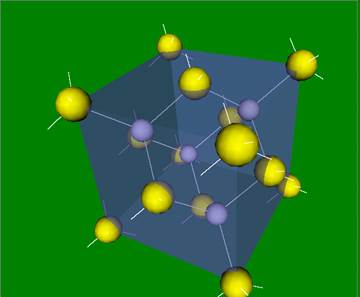
GaAs (ZnS, InAs, InP, AlAs, CdTe, HgTe)
Решетка GaAs состоит из двух ГЦК решеток смещенных на вектор [1/4,1/4,1/4].,
Решетка (GaAs, ZnS, InAs, InP, AlAs, CdTe, HgTe) 5x5x5
Множество кристаллов безгранично! Еще больше примеров Вы можете увидеть здесь:
Авторы: Е.В.Демидов, Ю.Н.Дроздов ИФМ РАН. Страничка подготовлена при поддержке Федеральной целевой Программы "Государственная поддержка интеграции высшего образования и фундаментальной науки".
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.