|
3.1.1. Возникновение потенциального
барьера. Контактная разность потенциалов.
 Электронно-дырочный переход -
основной элемент биполярных приборов, pn - переход создают в кристалле
изменением типа его проводимости, путем введения акцепторной и донорной
примеси. На рис. 19 схематически показан кристалл с резким pn переходом и
распределение акцепторной и донорной примеси в нем. Электронно-дырочный переход -
основной элемент биполярных приборов, pn - переход создают в кристалле
изменением типа его проводимости, путем введения акцепторной и донорной
примеси. На рис. 19 схематически показан кристалл с резким pn переходом и
распределение акцепторной и донорной примеси в нем.
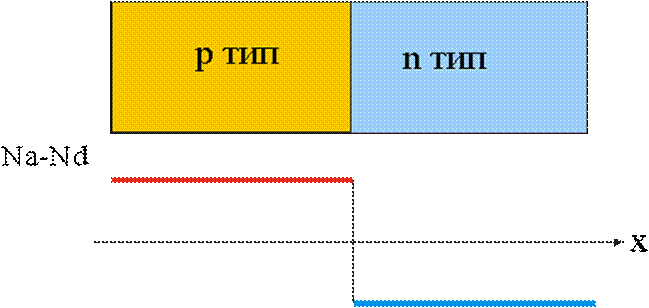 Рис. 19. Схема
кристалла с резким pn переходом (вверху) и распределение акцепторной (Na) и
донорной примеси в нем (Nd).
Рис. 19. Схема
кристалла с резким pn переходом (вверху) и распределение акцепторной (Na) и
донорной примеси в нем (Nd).
 Энергетическую диаграмму для pn
перехода можно получить достаточно просто, если воспользоваться положением
о том, что в системе, находящейся в равновесном состоянии, происходит
выравнивание средней энергии между ее частями и, соответственно, уровень
Ферми должен для всей системы иметь одно и то же значение. Энергетическую диаграмму для pn
перехода можно получить достаточно просто, если воспользоваться положением
о том, что в системе, находящейся в равновесном состоянии, происходит
выравнивание средней энергии между ее частями и, соответственно, уровень
Ферми должен для всей системы иметь одно и то же значение.
 Предположим, что у нас имеется две
изолированные полупроводниковые области p и n типов (мы можем получить их,
отрезав от левого и правого конца кристалла, показанного на рис. 19). Тогда
для этих областей можно построить энергетическую диаграмму, показанную в
верхней части рис. 20 (она аналогична рассмотренной ранее диаграмме рис.
5). Как иллюстрирует диаграмма, материал p и n типа отличается положением
уровней Ферми Fp и Fn и, соответственно, работой выхода Фp и Фn. Предположим, что у нас имеется две
изолированные полупроводниковые области p и n типов (мы можем получить их,
отрезав от левого и правого конца кристалла, показанного на рис. 19). Тогда
для этих областей можно построить энергетическую диаграмму, показанную в
верхней части рис. 20 (она аналогична рассмотренной ранее диаграмме рис.
5). Как иллюстрирует диаграмма, материал p и n типа отличается положением
уровней Ферми Fp и Fn и, соответственно, работой выхода Фp и Фn.
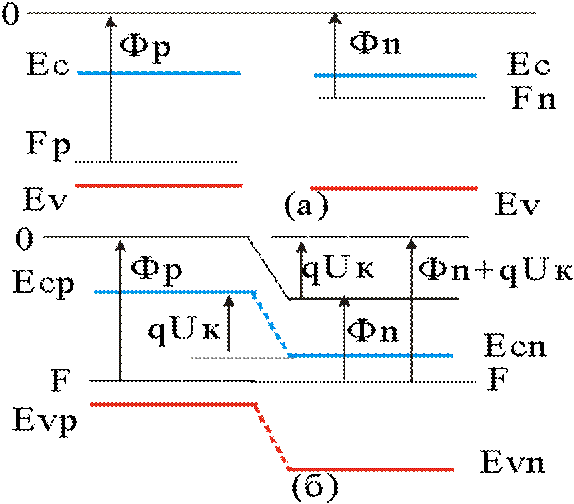 Рис. 20. Энергетическая
диаграмма: (а) изолированные p и n области, (б) pn - переход.
Рис. 20. Энергетическая
диаграмма: (а) изолированные p и n области, (б) pn - переход.
 Когда образуется pn переход, между
p и n областями происходит обмен электронами и дырками и энергией так, что
между областями устанавливается равновесие, и характеризующий равновесное
состояние уровень Ферми становится единым для всей системы, как это
показано на рис. 20 б. Области, находящиеся на значительном удалении от
места контакта p и n областей, не подвержены влиянию pn перехода, поэтому
их должна характеризовать энергетическая диаграмма, показанная на верхнем
рисунке (рис. 20а). Таким образом, условия сохранения свойств отдельных
материалов и единства уровня Ферми для всей системы приводят к появлению
скачка в области pn перехода. Этот скачок соответствует возникновению
потенциального барьера, который препятствует переходу основных носителей в
потенциальную область (дырок из p в n область и электронов из n в p
область). Потенциальный барьер возникает в результате появления внутреннего
электрического поля и соответствующей ему разности потенциалов Uк, которую
принято называть контактной. Когда образуется pn переход, между
p и n областями происходит обмен электронами и дырками и энергией так, что
между областями устанавливается равновесие, и характеризующий равновесное
состояние уровень Ферми становится единым для всей системы, как это
показано на рис. 20 б. Области, находящиеся на значительном удалении от
места контакта p и n областей, не подвержены влиянию pn перехода, поэтому
их должна характеризовать энергетическая диаграмма, показанная на верхнем
рисунке (рис. 20а). Таким образом, условия сохранения свойств отдельных
материалов и единства уровня Ферми для всей системы приводят к появлению
скачка в области pn перехода. Этот скачок соответствует возникновению
потенциального барьера, который препятствует переходу основных носителей в
потенциальную область (дырок из p в n область и электронов из n в p
область). Потенциальный барьер возникает в результате появления внутреннего
электрического поля и соответствующей ему разности потенциалов Uк, которую
принято называть контактной.
 Как видно из диаграмм рис. 20: Как видно из диаграмм рис. 20:
qUк = Фp - Фn =
Fn - Fp (39)
Т.е. контактная разность потенциалов равна разности
термодинамических работ выхода или разности энергии уровней Ферми в
материалах p и n типов. Чтобы рассчитать положение уровней Ферми,
воспользуемся формулами для концентраций электронов (дырок) в n и p
областях:
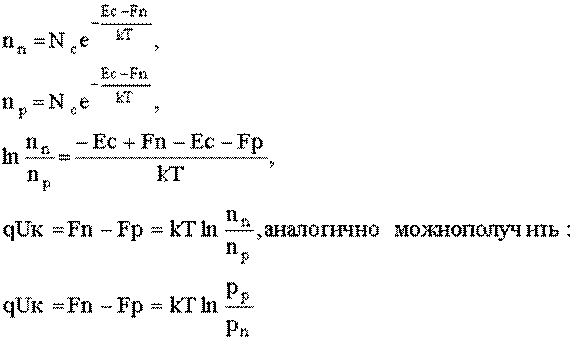 (40) (40)
 Поскольку концентрация основных
носителей примерно равна концентрации легирующей примеси (pp0 = Na, nn0 = Nd), и произведение равновесных
концентраций электронов и дырок в одной области при заданной температуре
равно квадрату концентрации собственных носителей заряда (18), то из (41)
получим: Поскольку концентрация основных
носителей примерно равна концентрации легирующей примеси (pp0 = Na, nn0 = Nd), и произведение равновесных
концентраций электронов и дырок в одной области при заданной температуре
равно квадрату концентрации собственных носителей заряда (18), то из (41)
получим:
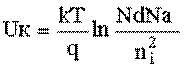 (42) (42)
 Таким образом, потенциальный
барьер в pn переходе тем выше, чем сильнее легированы p и n области. Таким образом, потенциальный
барьер в pn переходе тем выше, чем сильнее легированы p и n области.
 Рассмотрим, какова же физическая
природа явлений, приводящих к возникновению на границе между p и n
областями потенциального барьера. Если бы между p и n областями не было
контакта, то каждая из них была бы электронейтральна, при этом соблюдались
бы следующие условия: pp =
Na-, nn =
Nd+. При наличии между p и n областями контакта свободные
электроны будут уходить из n области в соседнюю, оставляя вблизи границы в
n области нескомпенсированный заряд положительных доноров - Nd+.
Свободные дырки будут уходить из p области в соседнюю, оставляя вблизи
границы в p области нескомпенсированный заряд отрицательных акцепторов - Na-.
Поскольку доноры и акцепторы связаны с решеткой, возникший двойной слой
заряда так же встроен в решетку и не может перемещаться. При этом в области
пространственного заряда (ОПЗ) возникает электрическое поле, направленное
от n области к p области, препятствующее переходу основных носителей через
границу областей. Чем больше переходит основных носителей, тем больше
нескомпенсированный заряд в ОПЗ, тем выше энергетический барьер,
препятствующий переходу. Равновесие наступает при некотором условии,
которое описывается формулами (41), (42). При этом следует отметить, что
основные носители из области пространственного заряда перебрасываются в
соседнюю область, где они становятся неосновными. В самой же области
пространственного заряда концентрация носителей мала (она близка к
собственной), поскольку все попадающие в ОПЗ носители выбрасываются из этой
области электрическим полем. Поэтому можно считать, что область
пространственного заряда обладает проводимостью на несколько порядков
меньшей, чем легированные p и n области. Поэтому в дальнейшем будем
считать, что сопротивление областей вне ОПЗ на несколько порядков меньше,
чем сопротивление ОПЗ и, если к полупроводниковой структуре с одним pn
переходом приложено внешнее напряжение, то оно падает, в основном на ОПЗ, а
в прилегающих к переходу p и n областях электрического поля практически
нет. Рассмотрим, какова же физическая
природа явлений, приводящих к возникновению на границе между p и n
областями потенциального барьера. Если бы между p и n областями не было
контакта, то каждая из них была бы электронейтральна, при этом соблюдались
бы следующие условия: pp =
Na-, nn =
Nd+. При наличии между p и n областями контакта свободные
электроны будут уходить из n области в соседнюю, оставляя вблизи границы в
n области нескомпенсированный заряд положительных доноров - Nd+.
Свободные дырки будут уходить из p области в соседнюю, оставляя вблизи
границы в p области нескомпенсированный заряд отрицательных акцепторов - Na-.
Поскольку доноры и акцепторы связаны с решеткой, возникший двойной слой
заряда так же встроен в решетку и не может перемещаться. При этом в области
пространственного заряда (ОПЗ) возникает электрическое поле, направленное
от n области к p области, препятствующее переходу основных носителей через
границу областей. Чем больше переходит основных носителей, тем больше
нескомпенсированный заряд в ОПЗ, тем выше энергетический барьер,
препятствующий переходу. Равновесие наступает при некотором условии,
которое описывается формулами (41), (42). При этом следует отметить, что
основные носители из области пространственного заряда перебрасываются в
соседнюю область, где они становятся неосновными. В самой же области
пространственного заряда концентрация носителей мала (она близка к
собственной), поскольку все попадающие в ОПЗ носители выбрасываются из этой
области электрическим полем. Поэтому можно считать, что область
пространственного заряда обладает проводимостью на несколько порядков
меньшей, чем легированные p и n области. Поэтому в дальнейшем будем
считать, что сопротивление областей вне ОПЗ на несколько порядков меньше,
чем сопротивление ОПЗ и, если к полупроводниковой структуре с одним pn
переходом приложено внешнее напряжение, то оно падает, в основном на ОПЗ, а
в прилегающих к переходу p и n областях электрического поля практически
нет.
 Диаграммы рис. 21 иллюстрируют
рассмотренные процессы. Область, в которой имеется электрическое поле
(ОПЗ), на рисунке обозначена d. Диаграммы рис. 21 иллюстрируют
рассмотренные процессы. Область, в которой имеется электрическое поле
(ОПЗ), на рисунке обозначена d.
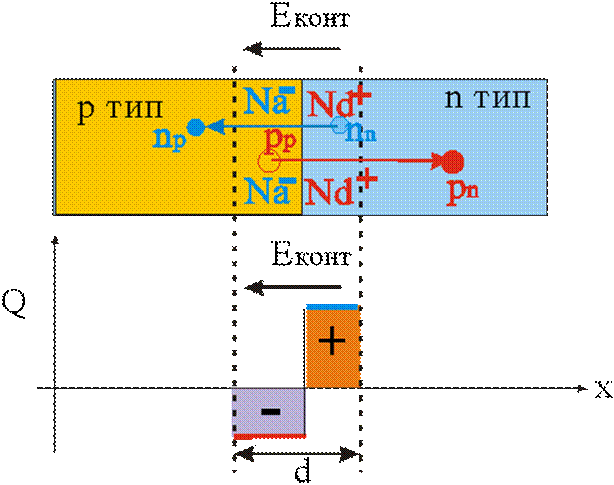 Рис. 21. Диаграмма,
поясняющая возникновение области пространственного заряда (двойного
заряженного слоя) в pn переходе.
Рис. 21. Диаграмма,
поясняющая возникновение области пространственного заряда (двойного
заряженного слоя) в pn переходе.
 Внимательно проанализировав
диаграмму рис. 21, можно еще раз убедиться, что направление контактного
электрического поля (Еконт) таково, что оно препятствует диффузии в
соседнюю область основных носителей заряда и способствует переходу
неосновных. Именно эта асимметрия потенциального барьера по отношению к
носителям различного типа в конечном счете и приводит к асимметрии
вольтамперной характеристики электронно-дырочного перехода относительно
полярности внешнего напряжения. При этом, при одной полярности внешнего
напряжения, поле внешней батареи будет складываться с внутренним полем
Еконт, увеличивая барьер, при другой вычитаться, уменьшая барьер. Внимательно проанализировав
диаграмму рис. 21, можно еще раз убедиться, что направление контактного
электрического поля (Еконт) таково, что оно препятствует диффузии в
соседнюю область основных носителей заряда и способствует переходу
неосновных. Именно эта асимметрия потенциального барьера по отношению к
носителям различного типа в конечном счете и приводит к асимметрии
вольтамперной характеристики электронно-дырочного перехода относительно
полярности внешнего напряжения. При этом, при одной полярности внешнего
напряжения, поле внешней батареи будет складываться с внутренним полем
Еконт, увеличивая барьер, при другой вычитаться, уменьшая барьер.
 Из формулы (42) следует, что чем
сильнее легированы области pn перехода, тем больше контактная разность
потенциалов. С физической точки зрения это понятно: с увеличением степени
легирования p области уровень Ферми приближается к валентной зоне, с
увеличением степени легирования n области уровень Ферми приближается к зоне
проводимости, в то же время как следует из диаграммы рис. 20, контактная
разность равна разности уровней Ферми в изолированных p и n областях.
Диаграмма рис. 22 иллюстрирует зависимость контактной разности потенциалов
от степени легирования областей. При увеличении степени легирования
областей контактная разность в пределе стремится к ширине запрещенной зоны
Eg. Из формулы (42) следует, что чем
сильнее легированы области pn перехода, тем больше контактная разность
потенциалов. С физической точки зрения это понятно: с увеличением степени
легирования p области уровень Ферми приближается к валентной зоне, с
увеличением степени легирования n области уровень Ферми приближается к зоне
проводимости, в то же время как следует из диаграммы рис. 20, контактная
разность равна разности уровней Ферми в изолированных p и n областях.
Диаграмма рис. 22 иллюстрирует зависимость контактной разности потенциалов
от степени легирования областей. При увеличении степени легирования
областей контактная разность в пределе стремится к ширине запрещенной зоны
Eg.
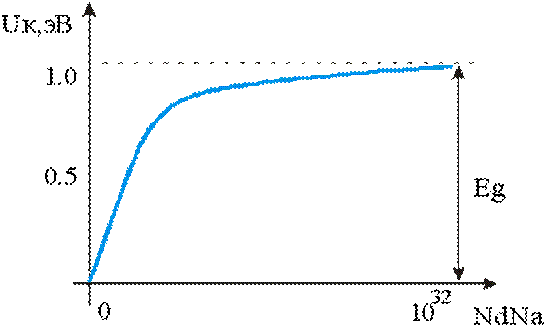 Рис. 22. Зависимость
контактной разности pn перехода от уровня легирования областей pn перехода
(Si, Т=300 К)
Рис. 22. Зависимость
контактной разности pn перехода от уровня легирования областей pn перехода
(Si, Т=300 К)
 Контактная разность также зависит
от температуры: с увеличением температуры она уменьшается. Этот результат
также понятен, если вспомнить, что с увеличением температуры увеличивается
вероятность межзонного возбуждения электронов, т.е. при высоких
температурах начинает доминировать собственная проводимость, а уровень
Ферми в собственных полупроводниках лежит вблизи середины запрещенной зоны.
Таким образом, поскольку с ростом температуры разность между уровнями Ферми
в изолированных p и n областях уменьшается, то, соответственно, должна
уменьшаться и контактная разность потенциалов, как это иллюстрирует рис.
23. Контактная разность также зависит
от температуры: с увеличением температуры она уменьшается. Этот результат
также понятен, если вспомнить, что с увеличением температуры увеличивается
вероятность межзонного возбуждения электронов, т.е. при высоких
температурах начинает доминировать собственная проводимость, а уровень
Ферми в собственных полупроводниках лежит вблизи середины запрещенной зоны.
Таким образом, поскольку с ростом температуры разность между уровнями Ферми
в изолированных p и n областях уменьшается, то, соответственно, должна
уменьшаться и контактная разность потенциалов, как это иллюстрирует рис.
23.
 Зависимость контактной разности
потенциалов pn переходов от температуры часто используют для создания
датчиков температуры. По чувствительности эти датчики будут уступать
датчикам, использующим температурную зависимость электропроводности
полупроводников (термисторы), однако к их достоинствам можно отнести
близкую к линейной зависимость контактной разности потенциалов от
температуры, что значительно облегчает их калибровку. Зависимость контактной разности
потенциалов pn переходов от температуры часто используют для создания
датчиков температуры. По чувствительности эти датчики будут уступать
датчикам, использующим температурную зависимость электропроводности
полупроводников (термисторы), однако к их достоинствам можно отнести
близкую к линейной зависимость контактной разности потенциалов от
температуры, что значительно облегчает их калибровку.
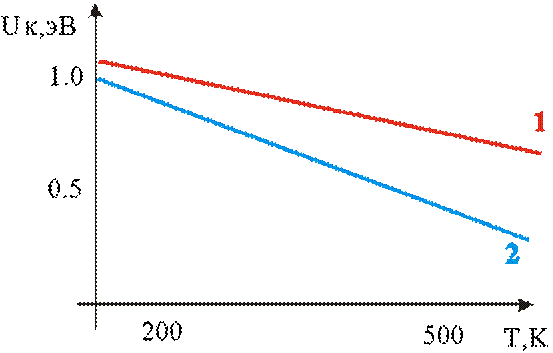 Рис. 23. Зависимость
контактной разности pn перехода от температуры при разном уровне
легирования областей (Si - кривая 1: NdNa=1032 , кривая 2: NdNa=1028)
Рис. 23. Зависимость
контактной разности pn перехода от температуры при разном уровне
легирования областей (Si - кривая 1: NdNa=1032 , кривая 2: NdNa=1028)
|

|