Электрический заряд. Теорема циркуляции вектора. Поведение во внешнем электрическом поле. Электрический ток

1.

Электрический заряд. В настоящее время известно, что в основе всего разнообразия явлений природы лежат четыре фундаментальных взаимодействия между элементарными частицами - сильное, электромагнитное, слабое и гравитационное. Каждый вид взаимодействия связывается с определенной характеристикой частицы. Например, гравитационное взаимодействие зависит от масс частиц, электромагнитное - от электрических зарядов. Электрический заряд частицы является одной из основных, первичных ее характеристик. Ему присущи следующие фундаментальные свойства:

1) электрический заряд существует в двух видах: как положительный, так и отрицательный;

2) в любой электрически изолированной системе алгебраическая сумма зарядов не изменяется, это утверждение выражает закон  сохранения  электриче-

ского заряда;

3) электрический заряд является релятивистски инвариантным: его величина не зависит от системы отсчета, а значит, не зависит от того, движется он или покоится.

Эти фундаментальные свойства электрического заряда имеют, как мы увидим, далеко идущие последствия.

Закон Кулона

 где ео—электрическая постоянная; q – заряды. r – расстояние между ними.

Принцип суперпозиции. Другой опытный факт, кроме закона Кулона, заключается в том, что напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:

где  - расстояние между зарядом q, и интересующей нас точкой поля.

2.

Напряженность поля

Принцип суперпозиции. Другой опытный факт, кроме закона Кулона, заключается в том, что напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:

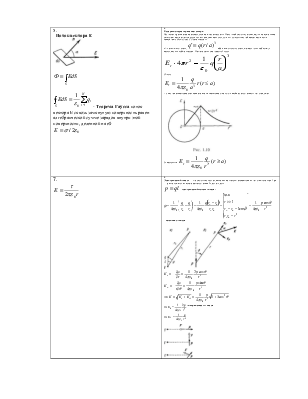
где  - расстояние между зарядом q, и интересующей нас точкой поля.

Вывод напряженности поля на оси тонкого равномерно заряженного кольца.

Поле на оси тонкого равномерно заряженного кольца. Заряд q> 0 равномерно распределен по тонкому кольцу радиусом а. Найти напряженность Е электрического поля на оси кольца как функцию расстояния z от его центра.

Легко сообразить, что в данном случае вектор Е должен быть направлен по оси кольца  (рис.  1.1). Выделим на кольце

около точки А элемент А1. Запишем выражение для составляющей от этого элемента в точке С:

где . Для всех элементов кольца r и а будут одними и теми же, поэтому интегрирование этого выражения сводится просто к замене  на q. В результате

Напряженность поля заряженной нити:

3.

Теорема циркуляции вектора Е.

 - интегральная

- дифференциальная

Поле обладающее этим свойством называется потенциальным, а значит любое электростатическое поле – потенциально.

 - разность потенциалов

-потенциал поля это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля.

Принцип суперпозиции

Работа по перемещению заряда

4.

5.

Поток вектора Е

- Теорема Гаусса поток вектора Е сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на е0

6.

Поле равномерно заряженного шара.

Пусть заряд q равномерно распределен по шару радиусом а. Поле такой системы, очевидно, также центрально-симметричное, поэтому и здесь для нахождения поля следует в качестве замкнутой поверхности взять концентрическую сферу. Сфера радиусом

r < а охватывает заряд  ибо в нашем случае заряды относятся как объемы, а последние как кубы радиусов. Поэтому согласно теореме Гаусса

Откуда

т. е. внутри равномерно заряженного шара напряженность растет линейно с расстоянием r от его центра.

За пределами

7.

8.

Электрический диполь — это система из двух одинаковых по модулю разноименных точечных зарядов + q и  — q. находящихся на некотором расстоянии l друг от друга.

 - электрический момент диполя-

- потенциал диполя

- напряженность диполя

9.

Диполь смотри 8.

Поведение во внешнем электрическом поле:

- момент сил действующих на диполь.

Энергия диполя в поле -

10.

Внутри проводника:

У поверхности проводника:

11.

 - Электроемкость проводника

-электроемкость уединенной сферы

12. Простейший конденсатор состоит из двух проводников (обкладок), расположенных на малом расстоянии друг от друга.

- электроемкость конденсатора.

- вывод электроемкости плоского конденсатора.

13. Смотри 12

- вывод электроемкости сферического конденсатора, где a и b – радиусы сфер

14. Смотри 12.

 - электроемкость цилиндрического конденсатора

15.

Диэлектриками (или изоляторами) называют вещества, практически не проводящие электрического тока. Это значит, что в диэлектриках в отличие, например, от проводников нет зарядов, способных перемещаться на значительные расстояния, создавая ток.

Молекулы могут быть полярными и неполярными. У полярных молекул центр «тяжести» отрицательного заряда сдвинут относительно центра тяжести положительных зарядов, в результате чего они обладают собственным дипольным моментом р. Неполярные же молекулы собственным дипольным моментом не обладают: у них центры тяжести положительного   и   отрицательного   зарядов   совпадают.

Объемные и поверхностные связанные заряды. В результате поляризации на поверхности диэлектрика, а также, вообще говоря, и в его объеме появляются не-скомпенсированные заряды. Нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называют поляризационными или связанными. Последним термином хотят подчеркнуть, что свобода перемещения таких зарядов ограничена. Они могут смещаться лишь внутри электрически нейтральных молекул.

Заряды, которые не входят в состав молекул диэлектрика, называют сторонними. Эти заряды могут  находиться  как  внутри,  так  и   вне  диэлектрика.

- поляризованность диэлектрика

-диэлектрическая восприимчивость

16.

 - вектор электрической индукции

 - диэлектрическая проницаемость в-ва

17.

18. 

 - энергия взаимодействия точечных зарядов

- полная энергия взаимодействия

 - энергия уединенного проводника

 - энергия конденсатора

 - объемная плотность энергии

19.

Электрический ток – упорядоченный перенос электрических зарядов.

Сила тока -

Плотность тока -

 - уравнение непрерывности

20.

 - Закон Ома

 - для неоднородной цепи

 - для замкнутой цепи

21. Первое правило – алгебраическая сумма токов, сходящихся в одной точке равна нулю.

Второе правило – алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопротивления равна сумме эдс действующих в этом контуре.

22.

23. - удельная тепловая мощность тока

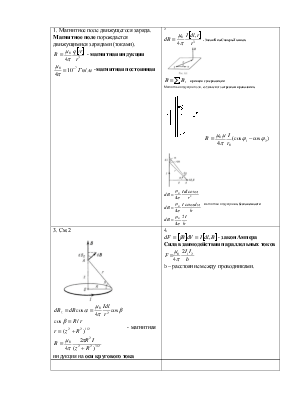
1. Магнитное поле движущегося заряда.

Магнитное поле порождается движущимися зарядами (токами).

 - магнитная индукция

 -магнитная постоянная

2.

 - Закон Био-Савара-Лапласа

 - принцип суперпозиции

Магнитная индукция поля, создаваемого отрезком проводника

 - магнитная индукция на бесконечности

3. См.2    - магнитная индукция на оси кругового тока

4.

 - закон Ампера

Сила взаимодействия параллельных токов

b – расстояние между проводниками.

5. Сила Лоренца – электромагнитная сила, действующая на заряд q.

Движение заряженной частицы в однородном магнитном поле:

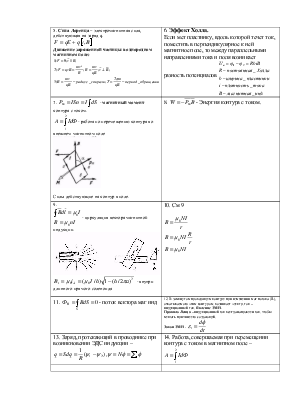
6. Эффект Холла.

Если мет пластинку, вдоль которой течет ток, поместить в перпендикулярное к ней магнитное поле, то между параллельными направлениями тока и поля возникает разность потенциалов

7.  - магнитный момент контура с током.

- работа по перемещению контура во внешнем магнитном поле

Силы действующие на контур в поле.

8. - Энергия контура с током.

9.

- циркуляция вектора магнитной индукции.

 - внутри длинного прямого соленоида

10. См 9

11. - поток вектора маг инд

12. В замкнутом проводящем контуре при изменении маг потока (B), охватываемого этим контуром, возникает электр. ток – индукционный ток. Явление ЭМИ.

Правило Ленца – индукционный ток всегда направлен так, чтобы мешать причине его создающей.

Закон ЭМИ -

13. Заряд, протекающий в проводнике при возникновении ЭДС индукции –

14. Работа, совершаемая при перемещении контура с током в магнитном поле –

15. Самоиндукция – изменение тока в контуре ведет к возникновению эдс индукции в этом же контуре.

Взаимная индукция - при протекании тока по первому контуру во втором возникает эдс индукции.

- Индуктивность длинного прямого соленоида

16.

- замыкание, размыкание цепи.

17.

-магнитное поле в веществе

18.

-вектор намагниченности в-ва

-напряженность маг поля

-маг восприимчивость

маг проницаемость

-циркуляция вектора напряженности

19.

Ферромагнетиками    называют   вещества (твердые), которые могут обладать спонтанной намагниченностью, т. е. намагничены уже при отсутствии внешнего магнитного поля. Типичные представители ферромагнетиков — это железо, кобальт и многие их сплавы.

Основная кривая намагничения. Характерной особенностью ферромагнетиков является сложная нелинейная зависимость J (Н) или В (Н). На рис. 7.12 дана кривая намагничения ферромагнетика, намагниченность которого при Н = 0 тоже равна нулю, ее называют основной кривой намагничения. Уже при сравнительно небольших значениях Н намагниченность J достигает насыщения Jнас Магнитная индукция  также растет с увеличением Н, а после достижения состояния насыщения В продолжает расти с увеличением