Использование циклов с предусловием в языке Pascal

Балтийский Государственный

Технический Университет

«ВоенМех»

имени Д.Ф. Устинова

Отчет

к лабораторной работе по информатике №3

На тему

Использование циклов с предусловием

в языке Pascal

Отчет выполнил студент

Факультета «И»

Суханов Александр

Группа И433

Санкт-Петербург 2003

Лабораторная работа по информатике №3

Тема: Использование циклов с предусловием в языке Pascal

Цель: Ознакомиться с понятием цикла и научиться использовать циклы с предусловием в языке Pascal.

Исходная задача: Вычислить сумму ряда F(x) = (x-1)/x + … + (x-1)^K/(k*x^K). Вычисления продолжать до тех пор, пока очередной член не станет меньшим или равным e.

Блок-схема алгоритма, решающего данную задачу:

 

 

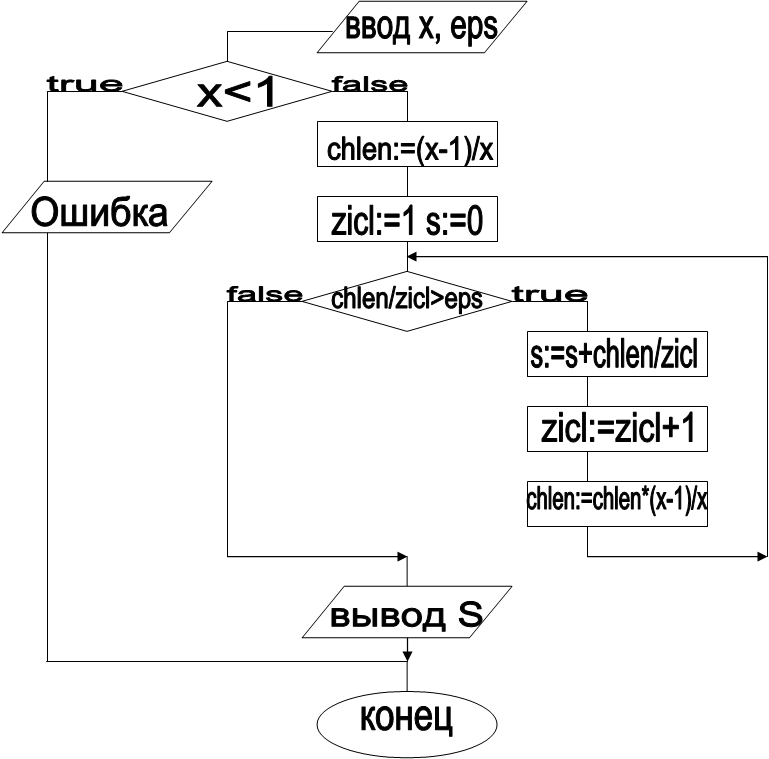
Пояснения к используемым данным:

X – исходное число

ZICL – обозначает номер элемента ряда

S – сумма ряда

CHLEN – вспомогательная переменная

Листинг программы, решающей данную задачу:

program lab3;

const eps = 0.0000001;

var x,chlen,s: real;

zicl: integer;

begin

write('введите X:'); readln(x);

if x<1 then

begin

writeln('Ошибка ввода');

halt;

end;

chlen:=(x-1)/x;

zicl:=1; s:=0;

while (abs(chlen)/zicl>eps) do

begin

s:=s+chlen/zicl;

inc(zicl);

chlen:=chlen*(x-1)/x;

end;

writeln('My log= ',s:15:9);

writeln('ln(x) = ',ln(x):15:9);

writeln('Погрешность: ', abs(s-ln(x)):10:9);

writeln('Точность:    ',eps:10:9);

end.

Тестовые данные к программе:

X=2.71

My log =  0.996948404

ln(x)     =  0.996948635

Погрешность 0.000000231

Точность        0.000000100

X=8

My log =  2.079440874

ln(x)     =  2.079441542

Погрешность 0.000000668

Точность        0.000000100

X=12

My log =  2.484905603

ln(x)     =  2.484906650

Погрешность 0.000001047

Точность        0.000000100

X=10000000

My log =  10.971134095

ln(x)     =  16.118095651

Погрешность 5.146961556

Точность        0.000000100

Вывод: Написанная программа вычисляет сумму ряда. Эта сумма ряда является значением натурального логарифма числа x, поэтому мы сравниваем в программе полученный результат с ln(x). Погрешность при больших X появляется из-за того, что стандартная функция вычисляет натуральный логарифм немного по другой схеме: в памяти ЭВМ заложена таблица значений некоторых натуральных логарифмов (вернее экспонент, которые легко инвертировать в логарифмы), а ln(x) вычисляется следующим образом: берется X и определяется, к какому заложенному в память X₀ он находится ближе. Найденный X₀ сохраняется. Далее вычисление суммы ряда идет по следующей формуле:  S= ln(X₀) + (X-X₀)/X + … + (X-X₀)^K/(K*X^K). Причем ln(X₀) – заданное число в таблице экспонент. Доказать вышесказанное можно путем замены единицы в формуле на некоторое число, допустим 10e7, а в конце цикла прибавлять к S ln(10e7):

-------------------chlen:=(x-10e7)/x;

zicl:=1; s:=0;

while (abs(chlen)/zicl>eps) do

begin

s:=s+chlen/zicl;

inc(zicl);

chlen:=chlen*(x-10e7)/x;

end;

s:=s+ln(10e7);

-------------------Тест этого алгоритма для X₀=10e7:

X=10e8

My log =  20.723264960

ln(x)     =  20.723265837

Погрешность 0.000000877

Точность        0.000000100

Вывод 2: В результате мы получили, что точность и погрешность имеют один порядок. Также погрешность можно уменьшить путем уменьшения eps, в принципе, мы можем сделать его равным нулю из-за того, что память компьютера конечна, то есть она не может хранить бесконечно малые числа, всегда существует предел. X может быть только положительным так как при X<0 этот ряд не будет сходится, то есть каждый член будет по модулю больше предыдущего.