Расчет торового, торосферического, эллиптического с жидкостью и конического с жидкостью днищ

Расчет рассматриваемых днищ

1. Торовое днище.

δ=17 мм, следовательно, меридиональные и тангенциальные напряжения

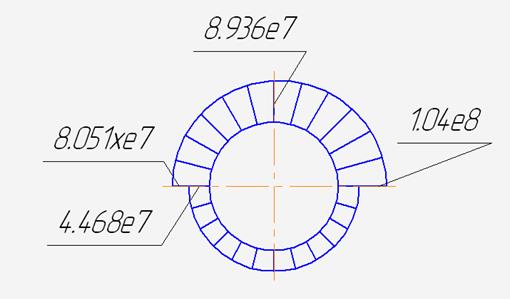
Вывод: тангенциальные напряжения постоянны вдоль меридиана, а меридиональные имеют максимум по внутреннему кольцу тора, равный 1.04*е8.

2. Торосферическое днище.

δ=46 мм, следовательно, меридиональные и тангенциальные напряжения

S1:=5.23 x 10⁷

 

 

 

 

Вывод: на полусферическом участке днища тангенциальные и меридиональные напряжения одинаковы и постоянны, наибольшие по величине отрицательные тангенциальные напряжения, возникающие при ύ=ύ₀, равны 1,113*е8.

3. Эллиптическое с жидкостью

δ=3 мм, следовательно, меридиональные и тангенциальные напряжения

Вывод: максимум меридиональных напряжений наблюдается в вершине днища и равен 2.435*е8, зависимость тангенциальных напряжений от положения точки на днище имеет причудливую форму, максимальное положительное их значение равно 2.435*е8, отрицательное – 8.934*е7.

4. Коническое с жидкостью

δ=0.83 мм, следовательно, меридиональные и тангенциальные напряжения

Вывод: как меридиональные, так и тангенциальные напряжения возрастают в направлении от основания днища, в каждом сечении тангенциальные напряжения преобладают над меридиональными. Их максимальные значения: 2.435*е8 и 1.255*е8.

5. Торосферическое с жидкостью

δ=23 мм, следовательно, меридиональные и тангенциальные напряжения

Вывод: максимальное значение меридиональных и положительных тангенциальных напряжений наблюдается в вершине днища и примерно равно 3.146*е6, наибольшие по величине отрицательные тангенциальные напряжения, возникающие при ύ=ύ₀, равны 1.929*е7.

6.  Эллиптическое днище, нагруженное постоянным давлением

δ=12 мм, следовательно, меридиональные и тангенциальные напряжения

Максимальное эквивалентное напряжение равно:

Это значение совпадает с максимальным тангенциальным (меридиональным) напряжением в вершине эллипса.

Расчет днища методом конечных элементов с помощью ANSYS

a)  Конечным элементом membrane 41:

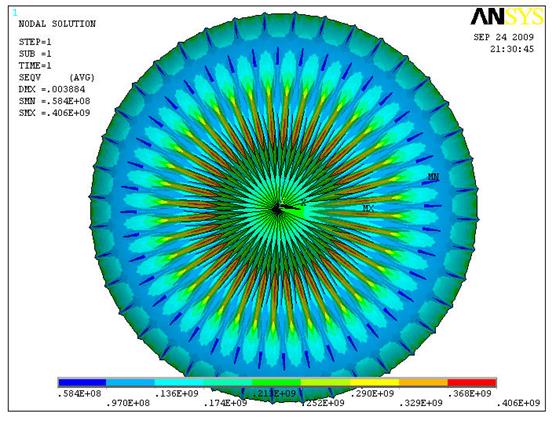
MINIMUM VALUES

NODE          1           1          20        2001        2001

VALUE  -0.44852E+07-0.24163E+09-0.45289E+09 0.59267E+08 0.58380E+08

MAXIMUM VALUES

NODE       1997          10          10          20          20

VALUE   0.11834E+09 0.91799E+08-0.18420E+07 0.44997E+09 0.40619E+09

b)  Конечным элементом shell 51:

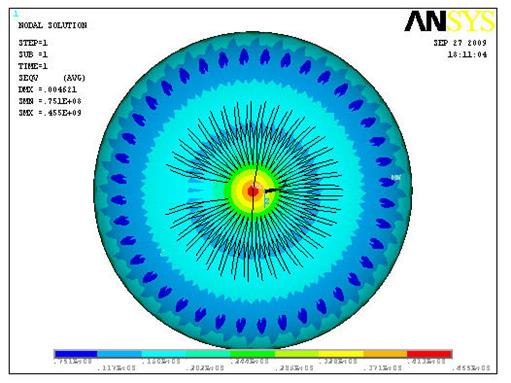
MINIMUM VALUES

NODE       2051        1830        1986        2051        2051

VALUE   0.77033E+08-0.42647E+07-0.19803E+09 0.76358E+08 0.75126E+08

MAXIMUM VALUES

NODE          1           1         601           1           1

VALUE   0.46109E+09 0.45507E+09 0.47411E+07 0.45896E+09 0.45497E+09

С) Конечным элементом shell 93:

MINIMUM VALUES

NODE         25        1575          12        1505        1505

VALUE  -0.20011E+07-0.25324E+08-0.16095E+09 0.49309E+08 0.45328E+08

MAXIMUM VALUES

NODE          1           1           1          12          12

VALUE   0.28996E+09 0.28693E+09 0.54552E+07 0.37377E+09 0.34010E+09

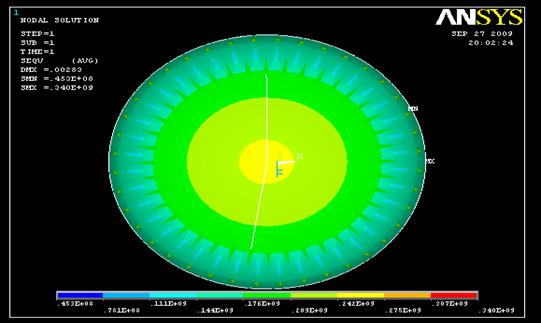
Вывод: значение максимальных эквивалентных напряжений, полученных аналитически по безмоментной теории отличается от значений, полученных расчетами в прикладной программе ANSYS, на незначительную величину, связанную с особенностями разбиения днища на конечные элементы.