



Лабораторная работа №2.
Вариант №22.
студента гр. И-564
Парфенова Дмитрия
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ
Цель работы – определение коэффициента вязкости жидкости.
Приборы и принадлежности: микроскоп МИР-12, стальные шарики малых размеров, секундомер, линейка, сосуд с жидкостью.
Рисунок установки:
Рабочие формулы:
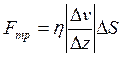 - закон вязкого трения
- закон вязкого трения
![]() - закон вязкого
трения для движущегося тела обтекаемой формы, где k – коэффициент пропорциональности.
- закон вязкого
трения для движущегося тела обтекаемой формы, где k – коэффициент пропорциональности. ![]()
Уравнение движения шарика в жидкости:
![]() , где
, где ![]() ,
, ![]() ,
, ![]()
Получаем: ![]()
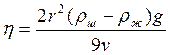
![]() Подставив
Подставив ![]() получаем
окончательную формулу:
получаем
окончательную формулу:
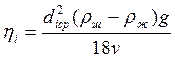 , i=1,2,…,6.
, i=1,2,…,6.
Таблица прямых измерений:
1.Определение размеров шариков
|
# опыта |
Номера шариков |
|||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|||||||||||||
|
n’ |
n’’ |
d1 |
n’ |
n’’ |
d2 |
n’ |
n’’ |
d3 |
n’ |
n’’ |
d4 |
n’ |
n’’ |
d5 |
n’ |
n’’ |
d6 |
|
|
1 |
||||||||||||||||||
|
2 |
||||||||||||||||||
|
3 |
||||||||||||||||||
|
di ср |
||||||||||||||||||
2. Определение установившейся скорости движения и коэффициента вязкости
|
Номер шарика |
I,м |
t,с |
v, м/с |
dср, м |
|
|
|
|
1 |
|||||||
|
2 |
|||||||
|
3 |
|||||||
|
4 |
|||||||
|
5 |
|||||||
|
6 |
|||||||
|
|
|||||||
![]() кг/м3
кг/м3 ![]() кг/м3
кг/м3 ![]() кг/м3
кг/м3
![]() м/с2
м/с2
Расчет погрешностей:
Для нахождения
погрешностей вначале исключаем известные систематические погрешности, затем
вычисляем среднее арифметическое результатов наблюдений, 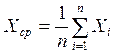 , и исключаем из серии измерений возможные
промахи. Для этого отбираем измерение резко отличающееся от остальных, и
проверяем, не является ли это измерение промахом.
, и исключаем из серии измерений возможные
промахи. Для этого отбираем измерение резко отличающееся от остальных, и
проверяем, не является ли это измерение промахом.
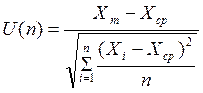 . Проверяем по табл. П2, находим, является
ли при данных n и a, полученное
значение U больше Uмах. Если да, то данное измерение является
промахом и его следует исключить из общего ряда.
. Проверяем по табл. П2, находим, является
ли при данных n и a, полученное
значение U больше Uмах. Если да, то данное измерение является
промахом и его следует исключить из общего ряда.
Также возможно
применить следующее правило: наблюдение можно отбросить, если его отклонение ![]() от среднего не менее чем в 2,5 раза
превосходит среднюю абсолютную погрешность по разбросу:
от среднего не менее чем в 2,5 раза
превосходит среднюю абсолютную погрешность по разбросу: 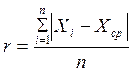 .
.
Затем вычисляем
оценку среднего квадратичного отклонения результата измерения: 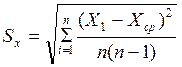
Определяем
доверительные границы случайной погрешности: ![]() , где
, где ![]() - коэффициент Стьюдента в зависимости от
надежности и числа измерений(табл. П1)
- коэффициент Стьюдента в зависимости от
надежности и числа измерений(табл. П1)
Вычисляем погрешность связанную с классом прибора:
А)![]() , где D – диапазон
шкалы, k – класс точности
прибора, %.
, где D – диапазон
шкалы, k – класс точности
прибора, %.
Б) ![]() , где c – цена
деления прибора, b – доля цены
деления, выбирается
, где c – цена
деления прибора, b – доля цены
деления, выбирается ![]()
В) погрешность округления.
Определяем границу
неисключенной систематической погрешности находим по формуле 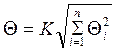 , где K=1.1 при а=0.95
, где K=1.1 при а=0.95
Сравниваем ![]() и
и ![]() :
:
Если ![]() < 0.8
< 0.8![]() , то
, то ![]() , a=0.95.
Окончательный результат:
, a=0.95.
Окончательный результат: ![]()
Если ![]() > 0.8
> 0.8![]() , то
, то ![]() .
. ![]()
Если 0.8<![]() <8, то необходимо вычислить
оценку суммарного квадратичного отклонения результата измерения:
<8, то необходимо вычислить
оценку суммарного квадратичного отклонения результата измерения: 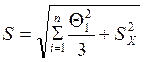 , затем вычислить эмпирический коэффициент
, затем вычислить эмпирический коэффициент 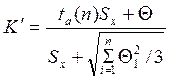 . Тогда
. Тогда ![]() .
Окончательный результат равен:
.
Окончательный результат равен: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.