Исследование свободных колебаний в колебательном контуре

Кукуев Сергей                                                                                                                     группа И 801

Лабораторная работа №54.

Исследование свободных колебаний в колебательном контуре.

Цель работы – исследование затухающих электромагнитных колебаний и определение характеристик затухания.

Приборы и принадлежности: колебательный контур и установка для возбуждения свободных колебаний в контуре, электронный осциллограф.

Схема установки:

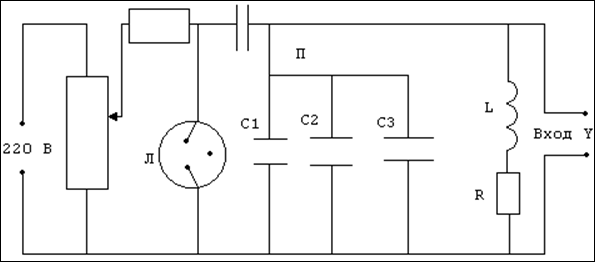
L – катушка индуктивности

C1, C2, C3 – конденсаторы

Л – неоновая лампа

П – переключатель для поочередного подключения C1, C2, C3

Вход Y – вход на электронный осциллограф.

Рабочие формулы и формулы погрешностей:

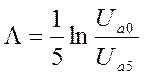Логарифмический декремент затухания.

Погрешность определения L:

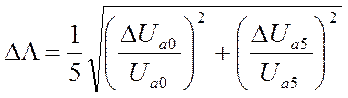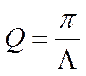
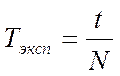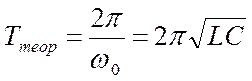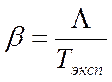 - добротность.       - коэффициент затухания  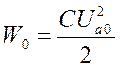     при t=0

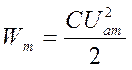при t=mT           

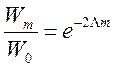
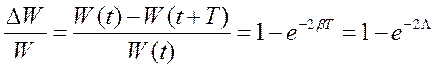
Таблица 1:

L =  ……  мГц,  C1 =  ……  мкФ,   С2 = ……  мкФ.

Конденсатор	m	Uam		Wm, Дж.	Wm/W0
		делен.	В		эксп.	теор.
С1 К =  . . .  В\делен.	0 1 2 3 4 5
С2 К =  . . .  В\делен.	0 1 2 3 4 5

Таблица 2:

Конденсатор	Число колебаний N	Цена деления t0, мс\делен.	Время t		Тэксп , мс
			делен.	мс
С1
С2

Таблица 3:

	L	DL	Т, мс.		b, с-1	Q	DW/W
			эксп.	теор.			эксп.	теор.
Контур с первым конденсатором С1
Контур со вторым конденсатором С2

Ответы на контрольные вопросы:

1. Колебательный контур состоит из последовательно соединенных конденсатора с емкостью С и катушки с индуктивностью L и омическим сопротивлением R. При свободных электромагнитных колебаниях в контуре полная энергия колебаний складывается из энергии электрического поля конденсатора и энергии магнитного поля катушки индуктивности. По закону сохранения энергии, убыль энергии электромагнитного поля за некоторый промежуток времени равна приращению за это же время количества выделившегося тепла, если можно пренебречь потерями на излучение.

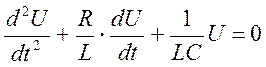 - дифф. уравнение затухающих колебаний.

2. Коэффициент затухания – это отношение R к L в дифф. уравнении затухающих колебаний. Он связывает сопротивление в цепи с индуктивностью катушки. Затухание колебаний описывается с помощью логарифмического декремента затухания, который характеризует уменьшение амплитуды за период. Логарифмический декремент затухания является характеристикой контура, так как зависит от параметров контура L, C, R:

                

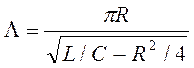
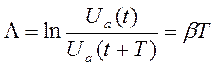
А добротность контура – это характеристика колебательного контура, обратно пропорциональная его логарифмеческому декременту затухания.

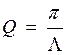
3. Энергия колебаний уменьшается с течением времени, т.к. на сопротивление R выделяется джоулево тепло. В момент времени, когда I=0, напряжение на конденсаторе достигает максимального (амплитудного) значения U_a и полная энергия колебаний равна энергии заряженного конденсатора:

Следовательно, полная энергия колебаний убывает по экспоненциальному закону: W(t)=W₀e^-2bt.

4. Напряжение с конденсатора подается на «Вход Y» электронного осциллографа. Отклонение луча ЭО по вертикали пропорционально поданному напряжению, причем одному большому делению вертикальной шкалы соответствует определенное напряжение, задаваемое переключателем «Вольт\делен». Развертка луча по горизонтали осуществляется таким образом, что одно большое деление горизонтальной шкалы луч проходит за определенное время t, задаваемое переключателем «Время\делен». Поэтому на экране осциллографа можно наблюдать в определенном масштабе зависимость U(t), т.е. график затухающих колебаний.