Структурный, кинематический и динамический анализ плоского шарнирно-рычажного механизма (частота вращения ведущего звена - 600 об/мин)

ного механизма и группы Ассура из звеньев 2 и 3 кинематической парой А в кинематическую цепь. Степень его подвижности

W = 3n – 2p_н – p_в= 3×3 – 2×4 = 1.

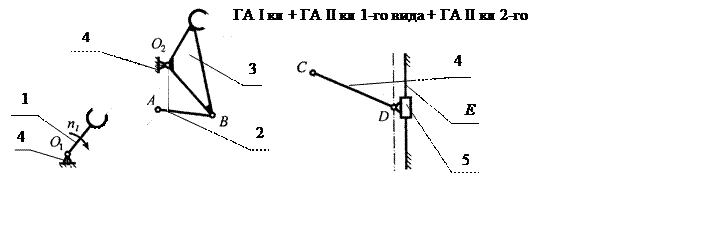Рисунок 5 – Структурная схема шестизвенного механизма

Формула строения механизма:   I(1) + II(1) + II(2).

Наивысший класс присоединенных групп – второй, поэтому механизм надо отнести ко II классу.

3.  Построение плана положений механизма

Сначала вычерчиваем 12 положений ведущего звена (см. чертеж). Определяем масштабный коэффициент плана положений по формуле

0,03/30 = 0,001

Определяем координаты шарниров и место положения направляющей, а также длины звеньев механизма на чертеже с учетом масштабного коэффициента:

0,13/0,001 = 130 мм; 0,08/0,001 = 80 мм;

0,1/0,001 = 100 мм; 0,14/0,001 = 140 мм;

0,11/0,001 = 110 мм;

Аналогично определяем остальные размеры: x₁ = 100 мм; x₂ = 120 мм; y₁ = 80 мм.

В качестве нулевого принимаем такое положение ведущего звена, при котором точка А занимает крайнее нижнее (левое) положение. Проводим окружность радиуса О₁А, делим ее на 12 равных частей, отмечая соответствующие точки (А₀, А₁, А₂, А₃ … А_{12; 0}). Для каждого из 12 положений ведущего звена методом засечек определяем положения всех остальных звеньев механизма.

Все построения выполняем сплошными тонкими линиями, после чего исследуемое положение механизма выделяем сплошной основной линией.

4.  Определение скорости и ускорения ползуна при помощи кинематических диаграмм

Построение диаграммы перемещений. В правой верхней части чертежа строим оси координат S_D – t(см. чертеж). На оси абсцисс откладываем отрезок / = 240 мм , измеряющий время одного оборота кривошипа. Делим его на 12 равных участков. Учитываем, что длина оси абсцисс не должна быть ограничена отрезком /, иначе на диаграммах скоростей и ускорений нельзя будет построить те части кривых, которые соответствуют половине крайних участков. Поэтому к 12 интервалам, на которые разбит весь цикл работы механизма, добавляем дополнительно 2 (6 – 7; 7 – 8), что в дальнейшем  позволит более точно построить графики функций скорости и ускорения на крайних интервалах 6 – 7; 7 – 8.

Для того чтобы откладываемые на диаграмме  перемещения по условиям компоновки уменьшить в два раза по сравнению с планом положений, принимаем коэффициент . Определяем величину масштаба диаграммы перемещений:

.

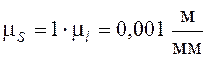Величину масштабного коэффициента оси абсцисс (масштаба времени) находим по формуле

.

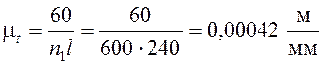В качестве начального принимаем положение 6, поскольку именно точка D₆является крайней на плане положений. В точках 7, 8, 9; 10, 11 ... 5 откладываем ординаты с учетом масштаба m_S, соответствующие перемещению ползуна В от крайнего левого положения D₆. До крайнего верхнего (правого) положения ординаты возрастают, после чего уменьшаются. Соединив последовательно соответствующие точки плавной линией, получаем диаграмму перемещений ведомого звена (ползуна).

Для построения диаграмм скорости и ускорения применяем метод графического дифференцирования. Величину полюсного расстояния Н₁ = 25 мм выбираем исходя из того, чтобы график v = f(t) поместился на месте, отведенном ему на чертеже.

Масштабный коэффициент скорости определяем по формуле

.

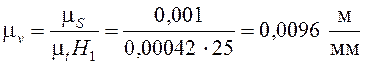Путем совместного анализа интегральной  и дифференциальной (v = f(t)) кривых убеждаемся в том, что все характерные зависимости между ними выполняются (см. чертеж).

Аналогично строим и диаграмму ускорений. На участке 3 – 4 диаграмма скорости имеет ярко выраженный экстремум, поэтому для более точного построения дифференциальной кривой этот участок разбиваем дополнительно на два интервала – до и после экстремума. Величину полюсного расстояния Н₂ принимаем равной 46 мм. Определяем масштабный коэффициент:

.

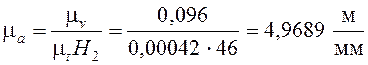Точка пересечения диаграммы а = f(t) с осью ординат была найдена при определении среднего ускорения на участках 5 – 6, 7 – 8, 8 –9, 9 – 10, 10 – 11 и изображения соответствующей кривой в правой части оси абсцисс