



причем деталей, обработанных на станке № 1, вдвое больше, чем на станке № 2. Найти вероятность того, что наугад взятая стандартная деталь изготовлена на первом станке. Задача решается с использованием теоремы:
1) Бернулли 2) вероятности произведения независимых событий
3) о полной вероятности 4)* Бейеса 5)Чебышева
7. В урне 3 красных и 4 синих шара. Из урны дважды вынимают по шару, не возвращая их в урну. Найти вероятность извлечения при втором испытании синего шара, если при первом испытании был извлечен красный шар.
1) ![]() 2)
2)
![]() 3)
3) ![]() 4)*
4)* ![]() 5)
5)
![]()
8. Среди 25 экзаменационных билетов 5 «хороших». Два студента по очереди берут по одному билету. Найти вероятность того, что второй студент взял «хороший» билет, если первый тоже взял «хороший».
1)* ![]() 2)
2)
![]() 3)
3) ![]() 4)
4) ![]() 5)
5) ![]()
9. Какова вероятность того, что из колоды в 36 карт будут вынуты подряд два туза?
1) 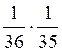 2)
2)
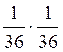 3)
3) ![]() 4)*
4)*
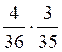 5)
5) ![]()
10. Считая вероятность отказа работы станка в течение смены равной 0,2, определить вероятность отказа в работе двух станков.
1)* 0,04 2) 0,1 3) 0,2 4) 0,4 5) 0,8
11. На перевозку груза направлены два автомобиля. Вероятность нахождения каждой из машин в исправном состоянии равна 0,8. Определить вероятность того, что в работе участвует хотя бы один из выделенных для этого автомобилей.
1) 0,16 2) 0,04 3) 0,36 4) 0,82 5)* 0,96
12. Вероятность рождения девочки равна 0,51. Для нахождения вероятности того, что среди 100 новорожденных будет ровно 50 девочек, необходимо использовать:
1) формулу полной вероятности 2) формулу Бейеса 3) локальную теорему Лапласа
4) теорему Чебышева 5)* формулу Бернулли
13. Дана задача: «40 % лежащих в ящике шаров белого цвета, остальные — красные. Какова вероятность того, что среди взятых наудачу 7 шаров окажется 4 шара белого цвета». Задача решается по формуле Бернулли, где:
1) n=100, k=40, p=![]() , q=
, q=![]() 2) n=40, k=7, p=
2) n=40, k=7, p=![]() , q=
, q=![]() 3) n=4, k=7, p=0,4, q=0,7
3) n=4, k=7, p=0,4, q=0,7
4)* n=7, k=4, p=0,4, q=0,6 5) n=7, k=4, p=0,6, q=0,4
14. Дана задача: «40 % лежащих в ящике шаров белого цвета, остальные — красные. Какова вероятность того, что среди взятых наудачу 7 шаров окажется 4 шара белого цвета». Задача решается по формуле Бернулли, где:
1) p=![]() , q=
, q=![]() 2) p=
2) p=![]() , q=
, q=![]() 3) p=0,4, q=0,7
3) p=0,4, q=0,7
4)* p=0,4, q=0,6 5) p=0,6, q=0,4
15. Дана задача: «40 % лежащих в ящике шаров белого цвета, остальные — красные. Какова вероятность того, что среди взятых наудачу 7 шаров окажется 4 шара белого цвета». Задача решается по формуле Бернулли, где:
1) n=100, k=40 2) n=40, k=7 3) n=4, k=7
4)* n=7, k=4 5) n=11, k=7
16. Дана задача: «40 % лежащих в ящике шаров белого цвета, остальные — красные. Какова вероятность того, что среди взятых наудачу 7 шаров окажется 4 шара белого цвета». По формуле Бернулли надо найти:
1)
P100(40) 2) ![]() 3)
P4(7) 4)* P7(4)
3)
P4(7) 4)* P7(4)
17. Дана задача: «40 % лежащих в ящике шаров белого цвета, остальные — красные. Какова вероятность того, что среди взятых наудачу 7 шаров окажется 4 шара белого цвета». По формуле Бернулли надо найти:
1) 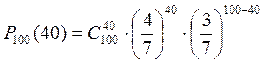 2)
2) 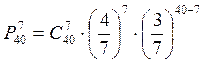
3) ![]() 4)*
4)* ![]()
5) ![]()
18. Дана
задача: «Вероятность изготовления детали первого сорта на данном станке равна 0,8. Найти вероятность
того, что среди наугад взятых 100 деталей окажется 75 деталей первого сорта». Применяя
локальную теорему Лапласа 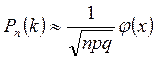 , находим x, равное:
, находим x, равное:
1)* 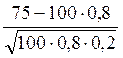 2)
2) 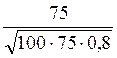 3)
3) 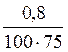
4) 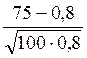 5)
5) 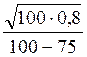
19. Для нахождения вероятности того, что при 100 выстрелах произойдет 80 попаданий, если вероятность поражения цели при одном выстреле равна 0,8, используется:
1) интегральная теорема Лапласа 2)* локальная теорема Лапласа
3) формула полной вероятности 4) классическое определение вероятности
5) формула Бейса
20. Для нахождения вероятности того, что число выпадения тройки при 4200 бросаниях игральной кости будет заключено от 100 до 200, используется:
1)* интегральная теорема Лапласа 2) локальная теорема Лапласа
3) формула полной вероятности 4) классическое определение вероятности
5) формула Бейеса
21.
Наивероятнейшее число т наступлений
события в nповторных независимых испытаниях удовлетворяет
неравенствам: ![]() , где p — вероятность появления
события в одном испытании. При n=10, p=0,5, q= 0,5 число m
равно:
, где p — вероятность появления
события в одном испытании. При n=10, p=0,5, q= 0,5 число m
равно:
1) m=4 2)* m=5 3) m=6 4) m=9 5) m=10
22. Значение
функции 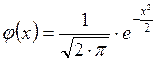 при
при ![]() равно:
равно:
1) ![]() 2)*
2)* ![]()
23. Значение функции Лапласа 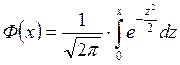 при
при ![]() равно:
равно:
1) ![]() 2)*
2)*![]()
24. Задача «Вероятность появления события в каждом из 2100 независимых
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.