Применение численных методов в компьютерном моделировании. Расчет базовой модели задней подвески

функции, соединяющей соседние точки принимается квадратный трехчлен, такая интерполяция называется параболической.

Распространенным видом интерполяции является использование кубических  сплайн-функций. Сплайн представляет собой модель гибкого тонкого стержня из упругого материала, закрепленного в двух соседних узлах интерполяции с заданными углами наклона альфа и бета так, чтобы  потенциальная энергия стержня была максимальной. Наиболее  известными методами аппроксимации является метод  наименьших квадратов, метод многочленов Чербышева, рядов Тейлора и т.д.

2 Алгоритмический анализ задачи

2.1 Полная постановка задачи

Работа автомобиля и трактора характеризуется переходными динамическими процессами, происходящими в их агрегатах и системах. Такие процессы происходят в трансмиссии, системе подрессоривания, сцепном устройстве и других агрегатах при трогании с места, разгоне, торможении, движении по неровностям опорной поверхности. В первом приближении эти процессы можно описать линейными дифференциальными уравнениями.

Так, дифференциальное уравнение, описывающее колебания задней части

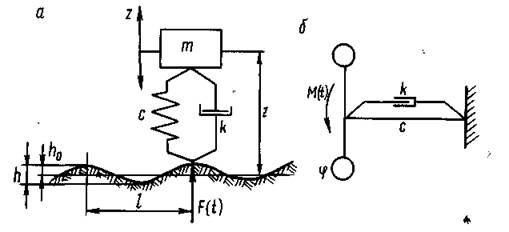
Рисунок 1 – схема механизма.

трактора при коэффициенте распределения масс ε=1 имеет вид на рисунке 1

В этих уравнениях т, I.— масса и момент инерции системы; k - коэффициент демпфирования в системе; с - жесткость системы; F(t), М (t) -  переменные внешние возмущения; z,φ— обобщенные координаты.

С точки зрения математики оба приведенных уравнения одинаковы. Таким образом, линейные и угловые колебания динамических систем с одной степенью свободы описываются линейными дифференциальными уравнении ми второй степени с постоянными коэффициентами.

Исходными данными для работы являются:

т — подрессоренная масса задней части трактора

l - длина неровности поверхности

с - суммарная радиальная жесткость задних шин

k - суммарный коэффициент демпфирования задних шин

v - скорость трактора

b0 — половина высоты неровности дороги

Необходимо:

·  С использованием системы MathCAD рассчитать значение функций перемещения, скорости и ускорения динамической системы задней подвески трактора. Построить графики этих функций.     

·  Исследовать   влияние   значений   изменяемого   параметра   на   амплитуду перемещения   задней   подвески   трактора,   для   этого   рассчитать   функцию перемещения движения трактора при различных значениях изменяемого параметра Построить графики зависимости перемещения задней подвески трактора  от времени.

·  Построить сводный график всех полученных функций перемещения на одном поле.

·  Построить   график  зависимости  локального  экстремума  перемещения   от варьируемого параметра.

·  Вычислить   аналитические   аппроксимирующие   функции   по   результатам   исследований   предыдущего    пункта.    Построить    графически    исходные аппроксимирующие зависимости. Сделать выводы по проведенным исследованиям

2.2 Описание математической модели

Получаем уравнение, описывающее колебания задней подрессоренной  части трактора, относительно старшей производной:

где  

Начальные условия:  t=0, z₀=0, z₀=0, v₀=5,2м/с.

2.3 Алгоритм решения задачи

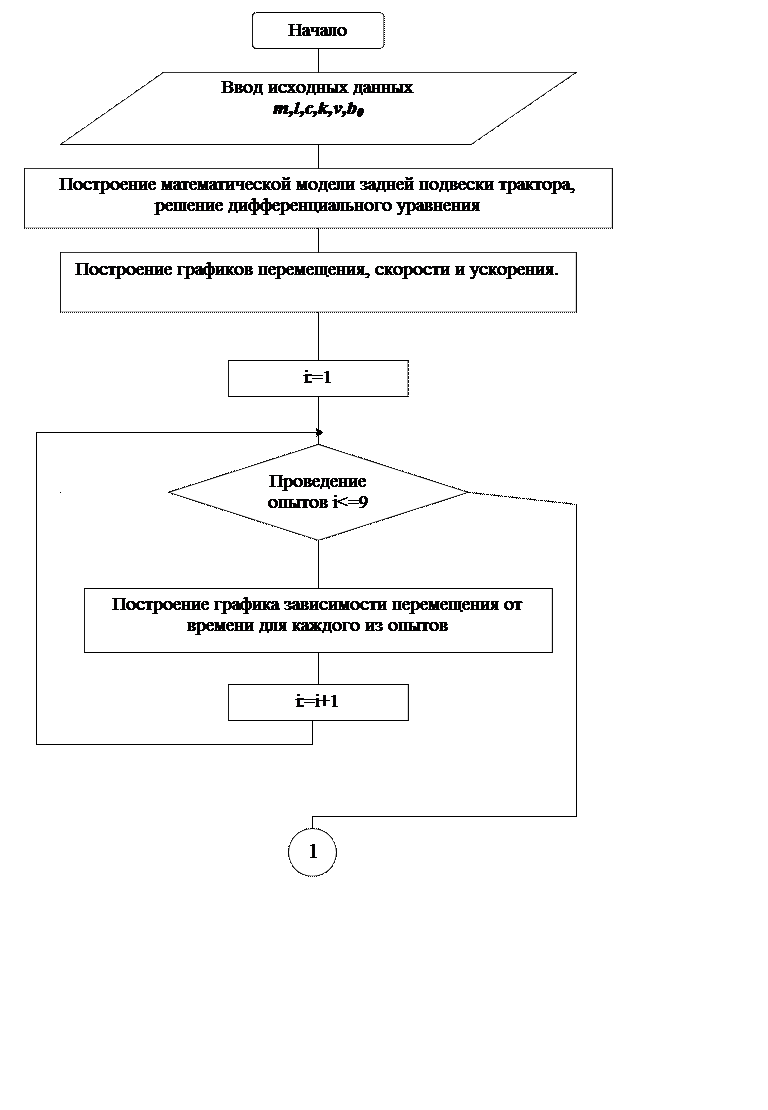
Последовательность шагов алгоритма решения задачи имеет следующий вид:

·  Задать исходные данные;

·  Рассчитываем промежуточные данные ω, ν, b(t), b

·  Решение системы дифференциальных уравнений для задней подвески трактора.

·  Провести 9 опытов для задней подвески трактора с изменением массы остова трактор от 2000 кг по 3300 кг на 100 кг.

·  Построение сводного графика.

·  Нахождения максимального значения отклонения массы для каждого опыта.

·  Проведения аппроксимацию опытов

·  Вывод графика результатов опытов и аппроксимирующей зависимости

Данный алгоритм может быть представлен  в виде графической схемы, приведенной в пункте 2.4

Реализация данного алгоритма в MathCad приведена в приложении.

2.4 Графическая схема задачи

Нахождения максимальных значений отклонений массы для каждого опыта

Выполнение аппроксимации результатов опытов

3 Описания реализации задачи в  MathCAD

3.1 Описание базовой модели задней подвески

Реализация расчета базовой модели задней подвески начинается с ввода исходных данных:

Исходными данными для работы являются:

m=2380 кг — подрессоренная масса задней части трактора

l=1 м - длина неровности поверхности

с=400000 Н/м - суммарная радиальная жесткость задних шин

k=5500 Нс/м - суммарный коэффициент демпфирования задних шин

v=5.2 м/с - скорость трактора

b0 =0,015 м— половина высоты неровности дороги

Расчета промежуточных данных

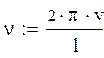частота возмущающей силы.

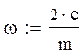 коэффициент упругости для задней  рессоры.

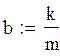         коэффициент сопротивления для задней  подвески. 

Для решения дифференциального уравнения  второго порядка