Исследования и изобретательство в машиностроении: Практическое пособие к лабораторным работам

отверстия могут находиться внутри поля допуска (скажем, составлять 60,012 мм). В этом случае была бы сделана ошибка первого рода. Очевидно, что когда размеры изделия находятся вблизи границ поля допуска, всегда есть вероятность сделать ошибку первого или второго рода.

Казалось бы, что наиболее опасна ошибка второго рода — пропуск брака. Это действительно так, когда мы имеем дело с очень ответственными изделиями (например, в авиа- или автомобилестроении). В этом случае иногда лучше забраковать 100 хороших изделий, чем пропустить одно бракованное. Чем вернее хотим мы застраховать себя от ошибок второго рода, тем больше (при неизменной точности измерений) делаем ошибок первого рода. Однако для менее ответственных изделий чересчур жесткий контроль, исключающий ошибки второго рода, нецелесообразен. Выбор экономически целесообразной системы измерений и браковки во всех случаях чрезвычайно важен.

5. Выбрать  метод оценки случайных ошибок измерений

В отличие от систематических погрешностей измерений случайные погрешности исключить нельзя, но с помощью методов теории вероятностей и математической статистики можно учесть их влияние при определении истинного значения измеряемой величины.

Случайные погрешности результатов эксперимента можно рассматривать как разновидность случайных величин (событий).

Полностью свойства случайной величины Х описываются функцией распределения F(x), которая определяет вероятность того, что случайная величина Х будет меньше х:

F(x) = P{X<x}.

Наряду с функцией распределения F(x), называемой интегральной, применяется и дифференциальная, обычно называемая плотностью распределения:

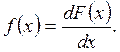
В практике точных измерений чаще всего имеет место нормальное, или равномерное  распределение случайных величин.

Функции распределения являются полными характеристиками случайных величин, но они не всегда удобны для практического использования. Поэтому при описании случайных величин применяют и их числовые характеристики — моменты случайных величин: начальные и централные.

Начальный  m_k и центральный m_k моменты k-го порядка определяются по формулам:

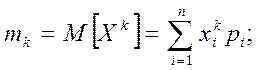
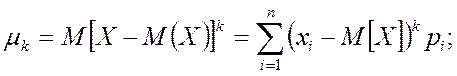
Чаще используется начальный момент первого порядка (k = 1) -математическое ожидание случайной величины:

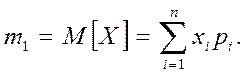      (1.1)

В указанных соотношениях р_i – относительная частота появления дискретной величины х_i  в выборке.  Предполагается, что 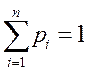  (т.е. рассматривается полная группа событий).

Из центральных моментов особенно важен момент второго порядка (k=2) – дисперсия случайной величины:

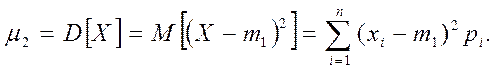     (1.2)

Положительный корень квадратный из дисперсии

носит название среднего квадратического отклонения случайной величины.

Значение s, характеризующее разброс случайных величин относительно их математического ожидания, наиболее часто используется для оценки случайной ошибки измерения.

Формулы (1.1) и (1.2) пригодны для оценки М [X] и D [X] генеральной совокупности, т. е. множества всех рассматриваемых единиц.

При измерениях обычно имеют дело с конечным подмножеством генеральной совокупности (n = 1...30), которое называют выборкой. Выборочные значения М [X] и D [X], обозначаемые обычно  (среднее арифметическое значение) и s², рассчитывают по формулам:

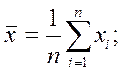
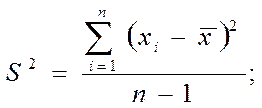  (1.3)

Если  n > 30, то 

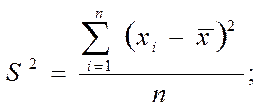  (1.4)

где п — число измерений или объем выборки.

Для оценки случайных ошибок измерений используют иногда коэффициент вариации u и среднюю арифметическую ошибку r_n:

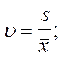
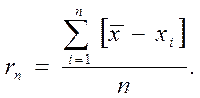
При достаточно большом числе наблюдений (практически при n >30) имеют место соотношения: s =1,25r_n   или  r_n = 0,8s.

По значениям s и  можно проверить, принадлежат резко выделяющиеся результаты измерений к данной генеральной совокупности или же вызваны грубыми погрешностями и их следует отбросить