Исследование и расчёт переходных процессов в объёмном гидроприводе с разветвлённой сетью трубопроводов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО

Факультет автоматизированных и информационных систем

Кафедра «Информационные технологии»

РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине «Информатика»

на тему:     «Исследование и расчёт переходных процессов в объёмном гидроприводе с разветвлённой сетью трубопроводов»

Исполнитель:          студент гр. ГА-21

Лифанов С.В.

Руководитель:         Курочка К.С.                                                

Дата проверки:               _____________________

Дата допуска к защите: _____________________

Дата защиты:                  _____________________

Оценка работы:              _____________________

Подписи членов комиссии по защите курсовой работы: ______________________________

Гомель 2005

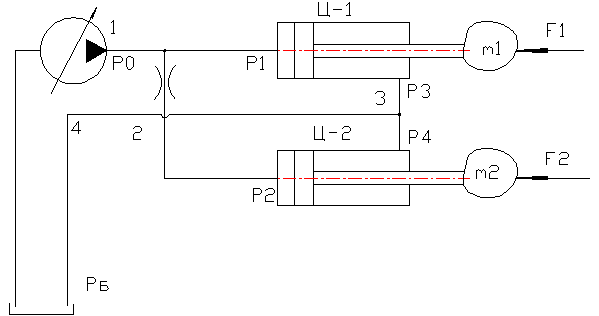
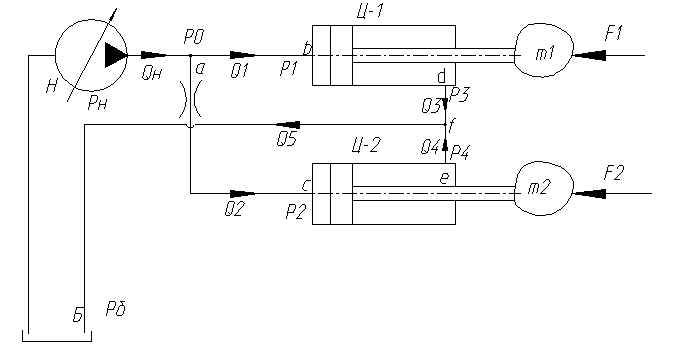
Рис. 1. Принципиальная гидравлическая схема привода

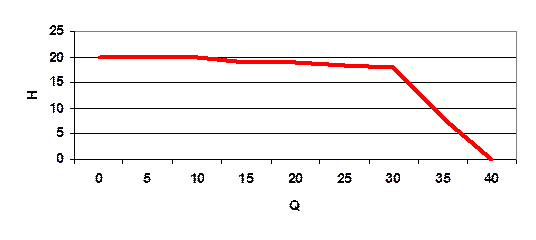
Рис. 2. Характеристика насоса

В соответствии с характеристикой насоса:

Кинематическая вязкость жидкости,

Плотность рабочей жидкости

Давление в баке

Коэффициент сопротивления дросселя

Характеристики трубопроводов:

Площадь на выпуск штока

Площадь на уборку штока

Рабочий ход штока

Приведенная к штоку масса

РАСЧЕТНАЯ ЧАСТЬ

1) Дифференциальное уравнение для участка трубопровода Н-a, см. рис. 3:

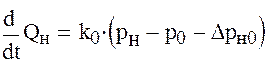
-давление в точке а;

-давление создаваемое насосом. Оно зависит от расхода жидкости в трубопроводе.

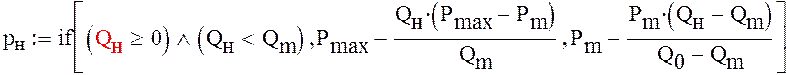
-потери на трение. Для определения  определим следующие величины:

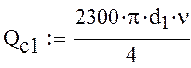
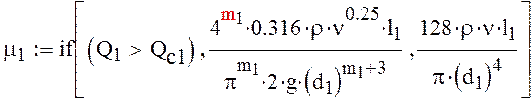
2)Дифференциальное уравнение для участка трубопровода a-b:

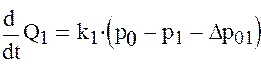
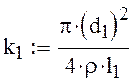-коэффициент учитывающий инерцию жидкости в трубопроводе

-гидравлические потери на трение.

Для определения  определим следующие величины:

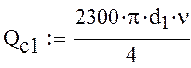
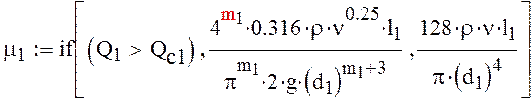
3) Дифференциальное уравнение для трубопровода на участке а-с:

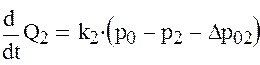
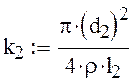-коэффициент учитывающий инерцию жидкости в трубопроводе

-давление в точке с;

-давление в точке а.

- суммарные потери, которые состоят из потерь на трение и потерь на дросселе.

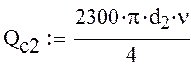
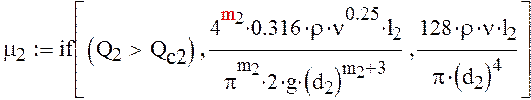
Изменение давления в дросселе:

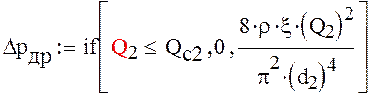
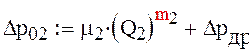
4) Дифференциальное уравнение для участка трубопровода d-f:

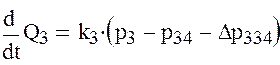
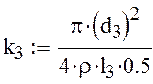-коэффициент учитывающий инерцию жидкости в трубопроводе

-давление в точке d;

-давление в точке f.

-потери давления на трение

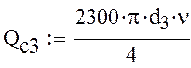
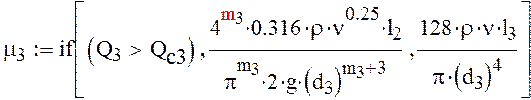
5) Дифференциальное уравнение для участка трубопровода e-f:

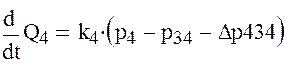
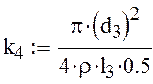-коэффициент учитывающий инерцию жидкости в трубопроводе

-давление в точке e;

-давление в точке f;

-потери давления на трение

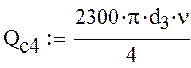
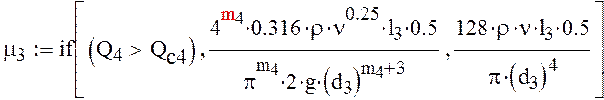
6) Дифференциальное уравнение для участка трубопровода f-Б:

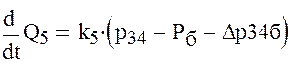
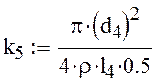-коэффициент учитывающий инерцию жидкости в трубопроводе

-давление в точке f;

-давление в баке;

-потери давления на трение

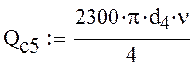
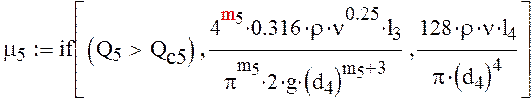
7) Дифференциальное уравнения неустановившегося движения поршня  гидроцилиндрах без учета сжимаемости жидкости в полостях

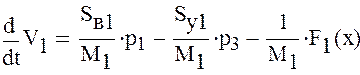
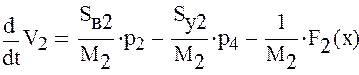
-активная сила вдоль штока гидроцилиндра. Будем считать, что она определяется следующей зависимостью.

-коэффициент жесткости штоков гидроцилиндров

Уравнение хода поршня

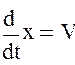
8) Уравнения расходов в трубопроводах

Зависимость расхода жидкости от скорости движения поршней гидроцилиндра

Подставив полученные зависимости  в уравнения расходов получим:

Продифференцируем  полученные уравнения

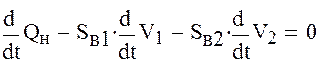
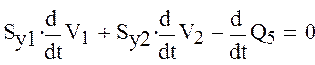
Подставим в эти уравнения ранее полученные дифференциалы

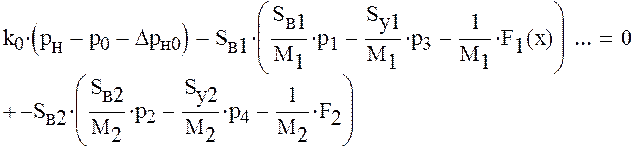
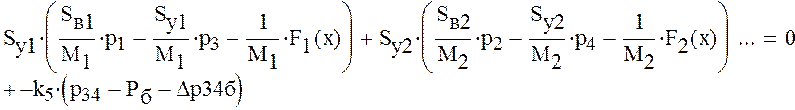
9) Продифференцируем следующие выражения

получим

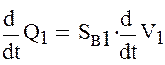
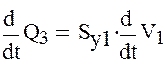
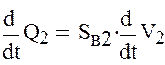
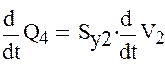
Получим следующую систему уравнений

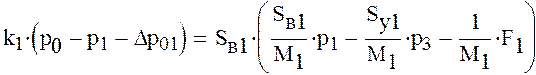
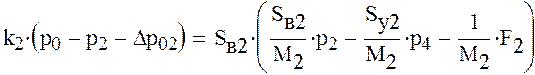
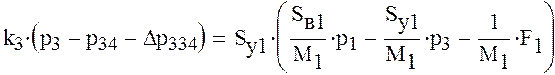
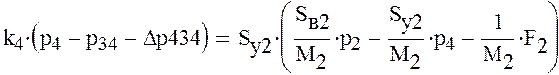
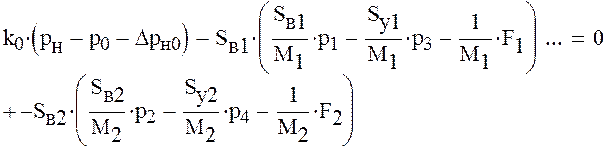
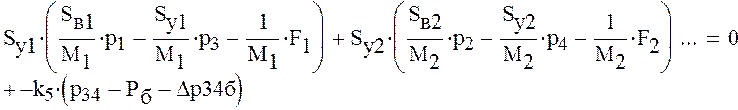
Решим полученную систему уравнений в начальный момент времени

при этом:

тогда

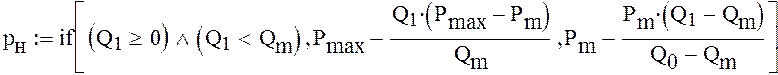
Обозначим

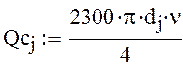
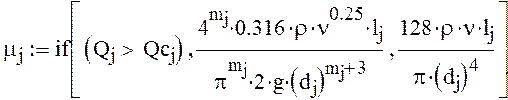
Так как, следовательно

Так как  состоит из потерь на  трение и на дросселе, то:

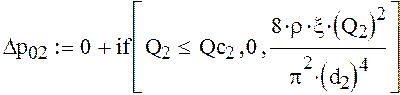
Получим систему линейных уравнений из шести уравнений с шестью неизвестными       .

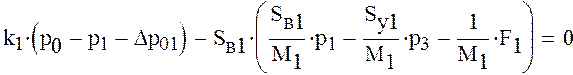
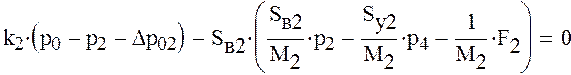
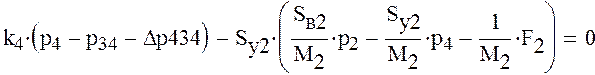
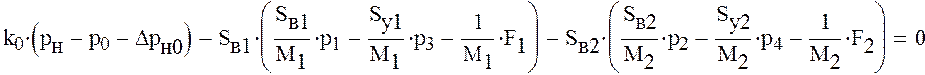
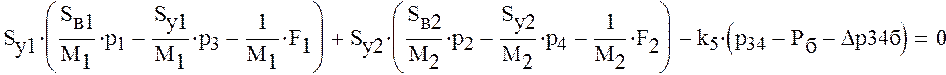
Преобразуем

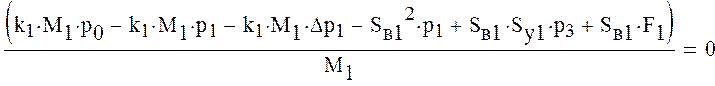
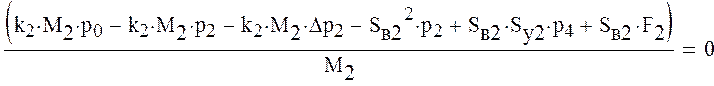
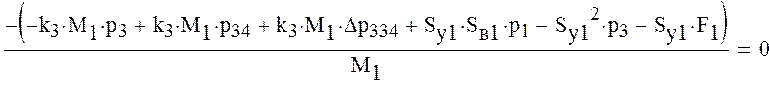
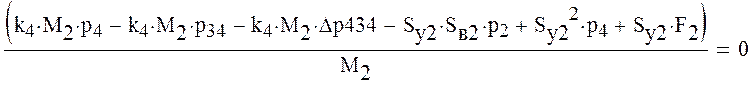
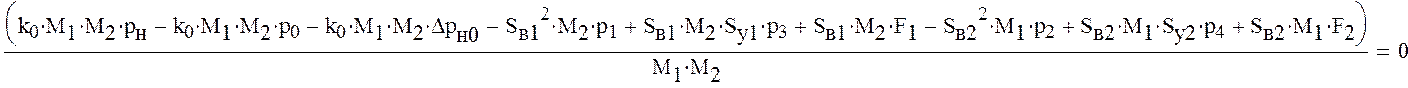
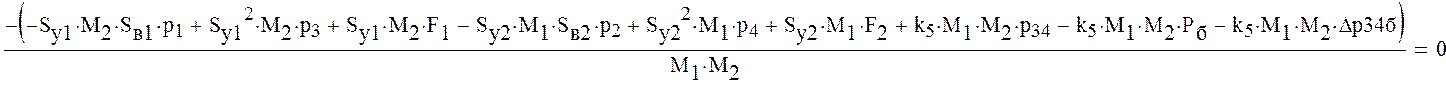
Перегруппируем уравнения системы таким образом, чтобы свободные члены были за знаком равенства

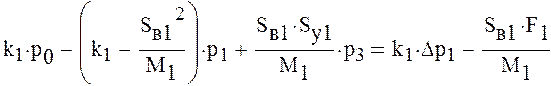
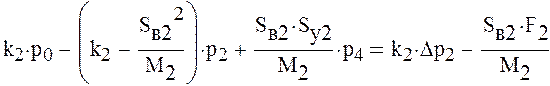
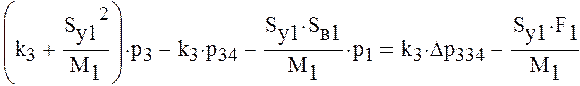
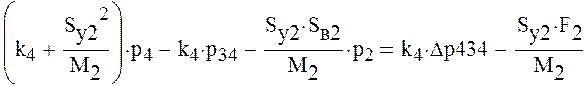
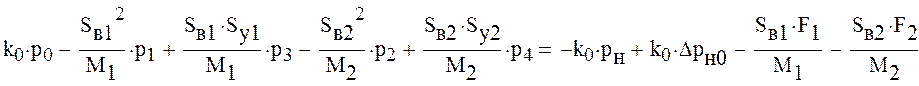
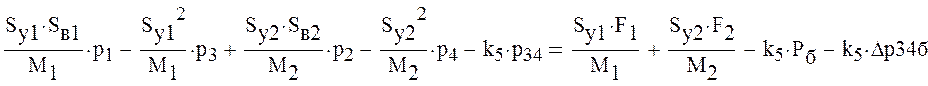
Решим полученную систему уравнений. Для этого составим матрицу коэффициентов при неизвестных давлениях и вектор свободных членов

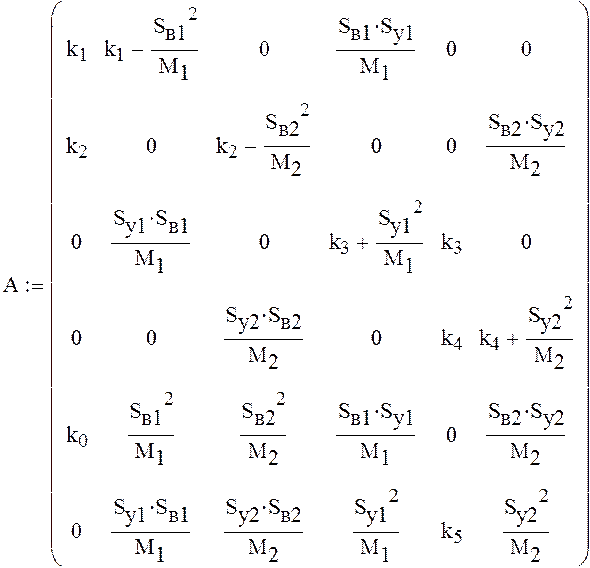
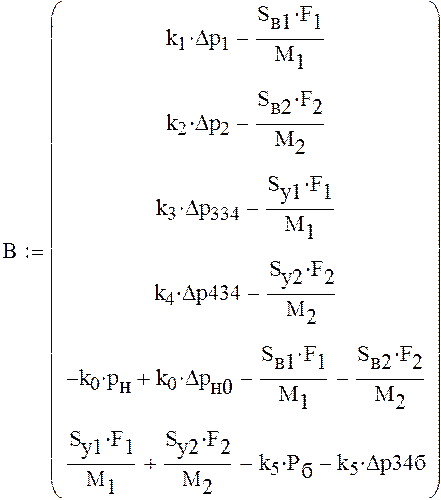
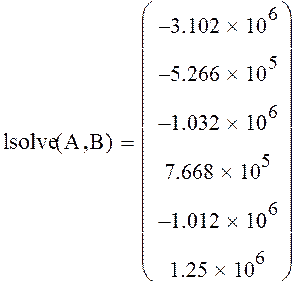
Найдем уравнения скорости движения поршней. Для  этого проинтегрируем дифференциальные уравнения неустановившегося движения поршней  гидроцилиндров.

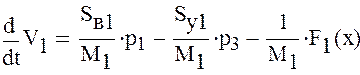
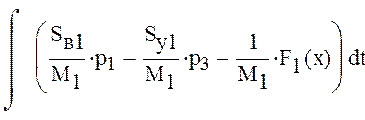
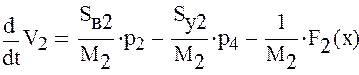
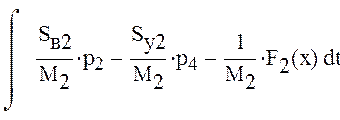
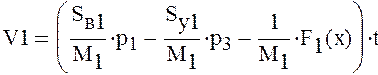
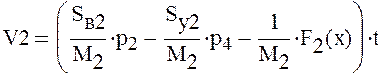
Для определения уравнения движения хода поршня проинтегрируем следующее уравнение

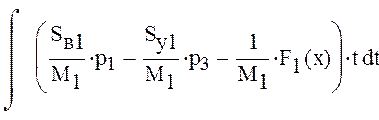
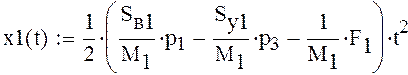
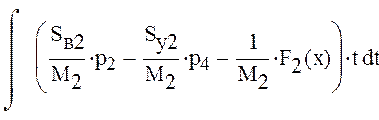
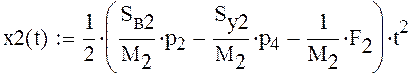
Построим графики хода штоков

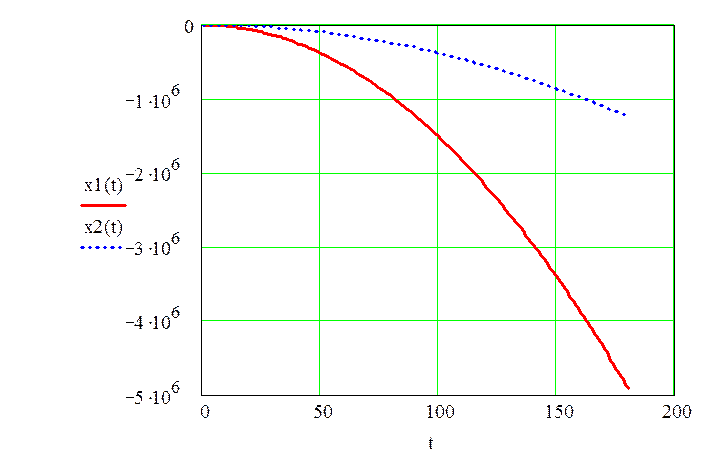
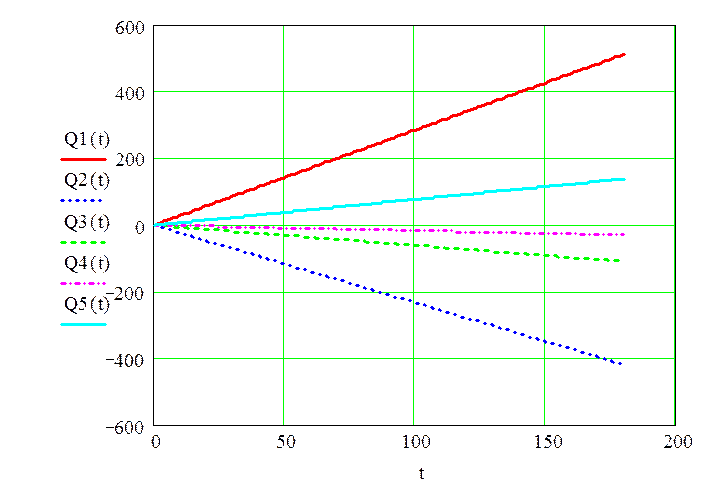
Построим графики расходов рабочей жидкости по всем линиям. Для этого продифференцируем уравнения расходов

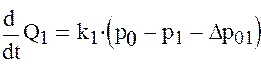
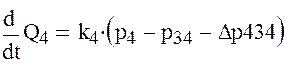
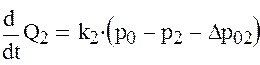
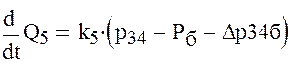
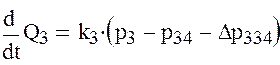
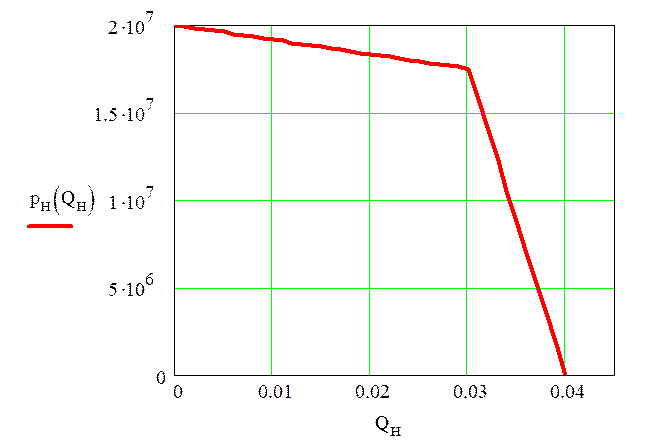
Построим график давления насоса:

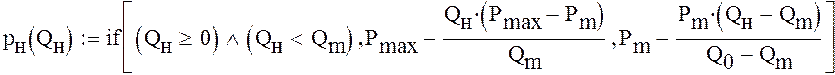
Влияние коэффициента сопротивления дросселя  на выход гидроцилиндра 2 на полный ход. Продифференцируем следующее уравнение

       получим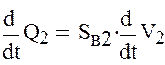          

или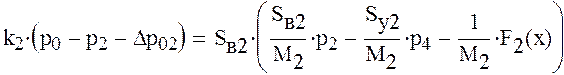 

Рассмотрим случай, когда  

примем     

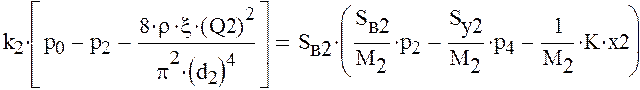
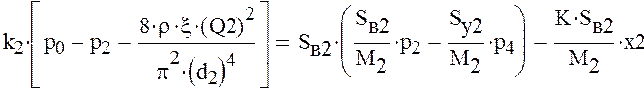
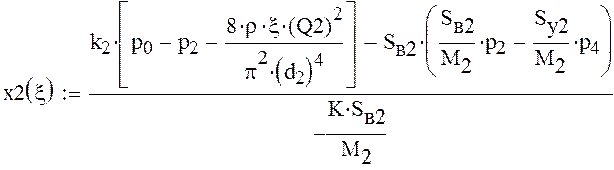
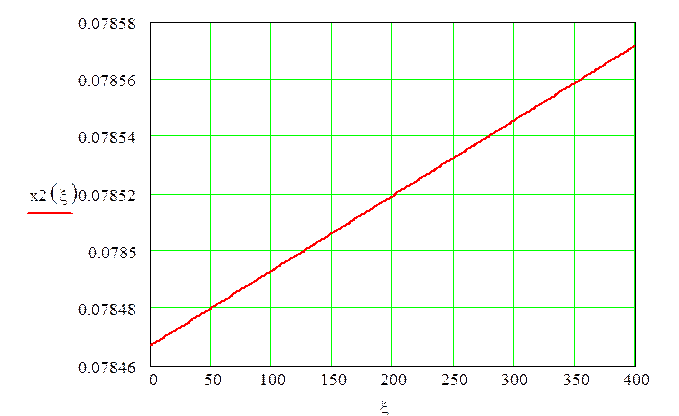
График зависимоти хода штока гидроцилиндра 2 от величины коэффициента сопротивления дросселя будет иметь вид: