Программирование прикладных задач на языке Паскаль: Задания к лабораторным и контрольным работам по курсу «Информатика»

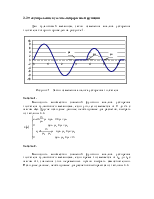
приведенный коэффициент вязкого сопротивления, вычисляется по формуле

Частота собственных колебаний p вычисляется по формуле:

Для исследования движения поршня необходимо знать следующие исходные данные: y₀– отклонение поршня от положения равновесия в начальный момент времени; с – жесткость пружины; D – диаметр цилиндра; d –  диаметр отверстия; z – число отверстий; m – масса поршня; H – высота поршня; µ - динамический коэффициент вязкости жидкости. Исходные данные приведены в таблице 3.3.

Таблица 3.3 – Исходные данные для задачи 3

3.3 Табулирование кусочно-непрерывной функции

Дан кулачковый механизм, закон изменения аналога ускорения толкателя которого приведен на рисунке 1.

Рисунок 1 - Закон изменения аналога ускорения толкателя

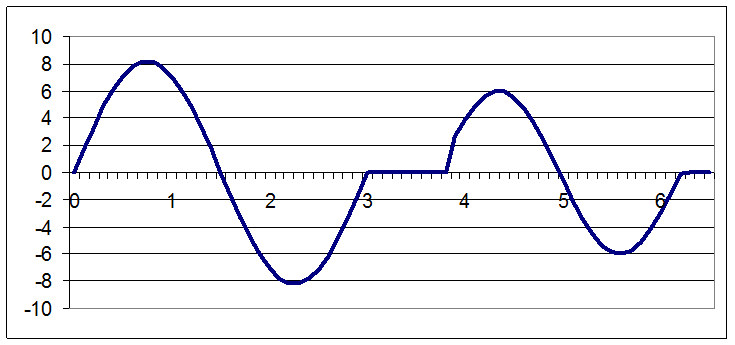
Задача 1.

Вычислить множество значений функции аналога ускорения толкателя кулачкового механизма, если угол φ изменяется от 0 до 2π с шагом Δφ. Другие исходные данные, необходимые для расчетов, выбрать из таблицы 3.3.

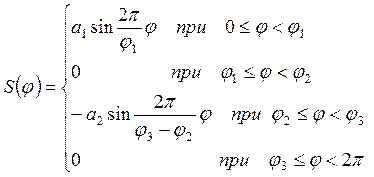
Задача 2.

Вычислить множество значений функции аналога ускорения толкателя кулачкового механизма, если время t изменяется от t_н до t_к с шагом Δt, значения этих переменных нужно выбрать самостоятельно. Исходные данные, необходимые для расчетов выбираются из таблицы 3.3.

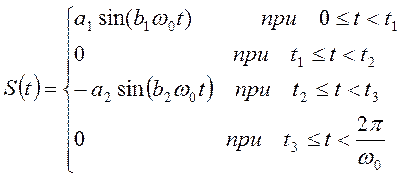
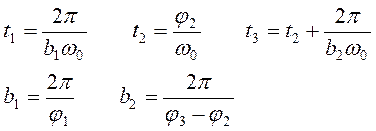
Таблица 3.3 – Исходные данные для задачи 2

4 Программирование прикладных задач с использованием одномерных массивов

4.1 Обработка элементов в одномерных массивах

Для предложенной задачи составить графическую схему алгоритма и написать программу. Исходные данные для расчетов подобрать самостоятельно.

Дана фигура (рисунок 2), которая может быть разбита на  прямоугольников высотой  и шириной .

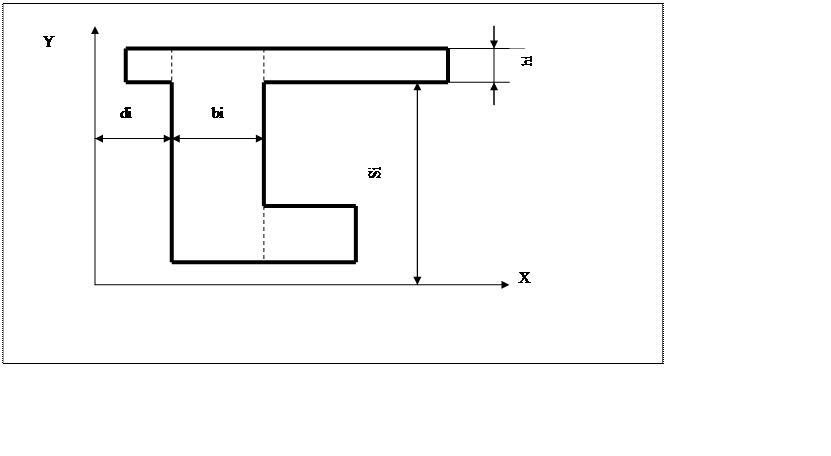
Рисунок 2 - Заданное сечение

Оси X и Y проводятся так, чтобы они были параллельны сторонам рассматриваемого сечения. Расстояния от осей X и Y до ближайших сторон прямоугольников обозначаются соответственно S_i и d_i. Координаты центра тяжести сложной фигуры определяются по формулам:

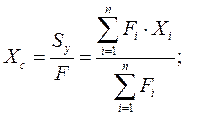
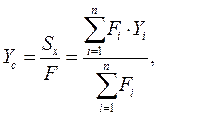
где S_x и S_y- статические моменты фигуры; F- площадь фигуры; F_i- площади отдельных простых частей; X_i и Y_i- координаты центров тяжести этих частей

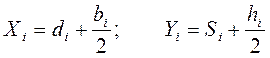
Моменты инерции сечения относительно осей X и Y определяются как сумма моментов инерции отдельных прямоугольников. При этом можно воспользоваться формулами преобразования при параллельном переносе осей:

 ;

.

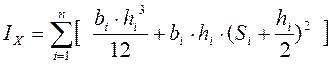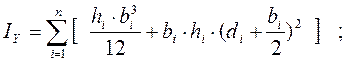
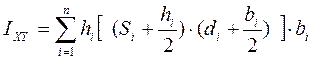Зная значения I_X, I_Y, I_XY, можно определить центральные моменты инерции:

;

.

Главные моменты инерции (,), угол наклона оси  к оси ( ) и радиусы инерции (,) определяются соответственно по формулам:

 ;         

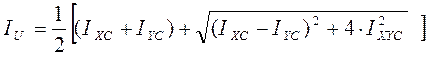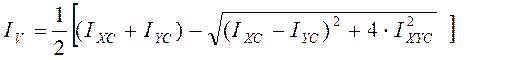
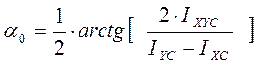
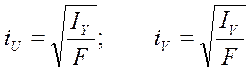
Вариант 1. Определить координаты центра тяжести Y_C сложной фигуры, состоящей из n участков.

Вариант 2. Определить момент  инерции I_X сечения сложной фигуры относительно оси X.

Вариант 3. Определить центральный момент инерции I_XC сложной фигуры.

Вариант 4. Определить координату X_C центра тяжести сложной фигуры, состоящей из n  участков.

Вариант 5. Определить главный момент инерции I_V сложной фигуры, разбитой на отдельные простые части.

Вариант 6. Определить центральный момент инерции I_YC сложной фигуры.

Вариант 7. Определить угол наклона оси U  к оси X_C – α₀.

Вариант 8. Определить координату центра тяжести X_C сложной фигуры.

Вариант 9. Определить главный момент инерции I_U сложной фигуры, разбитой на отдельные простые части.

Вариант 10. Определить момент  инерции I_Y сечения сложной фигуры относительно оси Y.

Вариант 11. Определить радиус инерции i_U сложной фигуры.

Вариант 12. Определить центральный момент инерции I_XYC сложной фигуры.

Вариант 13. Определить момент  инерции I_XY сложной фигуры.

Вариант 14. Определить радиус инерции i_V сложной фигуры.

Вариант 15. Определить координаты центра тяжести Y_C и X_C сложной фигуры, состоящей из n участков.

4.2 Обработка строк и столбцов двумерных  массивов

Для предложенной задачи составить графическую схему алгоритма и написать программу.

Три независимых эксперта проводили измерения шероховатости поверхности металлических образцов, полученных после обработки на станке с заданными параметрами. Результаты измерений представлены в виде матрицы значений независимых переменных и экспериментальных значений шероховатости поверхности. Первый столбец матрицы - номер опыта, второй и третий столбцы – значения независимых переменных: S – подача инструмента в мм/об; m – скорость м/с. В четвертом, пятом и шестом столбцах расположены эмпирические данные шероховатости поверхности, полученные тремя независимыми экспертами: (таблица 4.1.).

Таблица 4.1 – Результаты измерений шероховатости поверхности

Вариант 1. Найти максимальное значение шероховатости поверхности для всех опытов по всем измерениям экспертов.

Вариант 2. Найти минимальное значение шероховатости поверхности для всех опытов по всем измерениям экспертов.

Вариант 3. Сформировать массив из средних значений шероховатости поверхности для каждого опыта.

Вариант 4. Сформировать массив из максимальных значений шероховатости поверхности для каждого опыта.

Вариант 5. Сформировать массив из минимальных значений шероховатости поверхности для каждого опыта.

Вариант 6. Найти среднее значение шероховатости поверхности для всех