










точнее выбрано начальное приближение, тем быстрее функция root будет сходиться к точному значению.
Для
изменения точности, с которой функция root
ищет корень, можно изменить значение встроенной переменной TOL. Переменная TOL по
умолчанию равна 0.001. Если значение TOL
уменьшать, то процесс нахождения корня будет замедляться, но ответ будет более
точен. Например, уравнение ![]() имеет
два корня 1.2 и 1.25, при различных значениях TOLкорень определяется с
некоторой погрешностью.
имеет
два корня 1.2 и 1.25, при различных значениях TOLкорень определяется с
некоторой погрешностью.
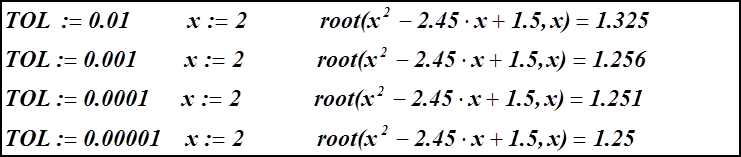
Уменьшать TOL желательно и в случае, когда два нулевых корня расположены близко друг от друга, чтобы различить их. Например, для предыдущего уравнения начальные условия определим в виде диапазонной переменной и установим различные значения TOL.


1.2. Нахождение корней полинома с применением функции polyroots
Для нахождения нулевых корней степенного полинома вида:
![]() , (1.3)
, (1.3)
лучше
использовать функцию polyroots, нежели
root. В отличие от функции root,
функция polyroots не требует начального приближения и вычисляет все
корни уравнения, как вещественные, так и комплексные. Аргумент функции polyroots состоит из вектора коэффициентов полинома длиной (n+1),
в котором коэффициенты полинома начинаются с константы ![]() .
Функция polyroots возвращает
вектор длиной n, состоящий из корней полинома.
.
Функция polyroots возвращает
вектор длиной n, состоящий из корней полинома.
На рис. 1.1-1.2 приведены примеры нахождения корней полиномов.
1.3. Решение систем алгебраических уравнений методом решающего блока
MathCAD имеет возможность решать системы алгебраических уравнений вида:
![]() (1.4)
(1.4)
c неизвестными ![]() . Максимальное количество уравнений и переменных равно
пятидесяти.
. Максимальное количество уравнений и переменных равно
пятидесяти.
Для решения системы уравнений необходимо выполнить следующие действия:
· Задать начальные приближения для всех неизвестных, входящих в систему уравнений.
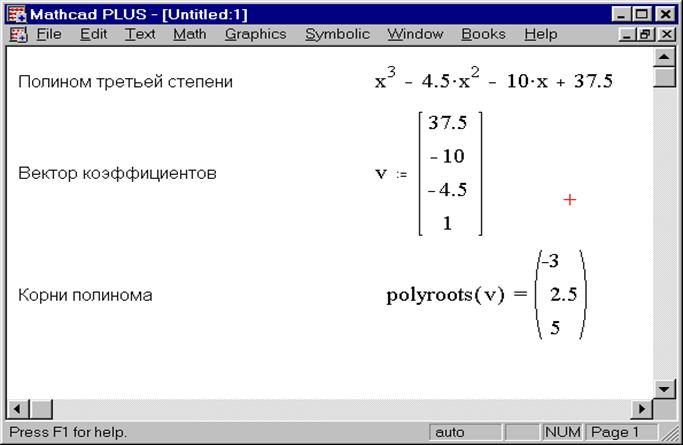
Рис. 1.1. Использование функции polyroots для поиска вещественных корней полинома
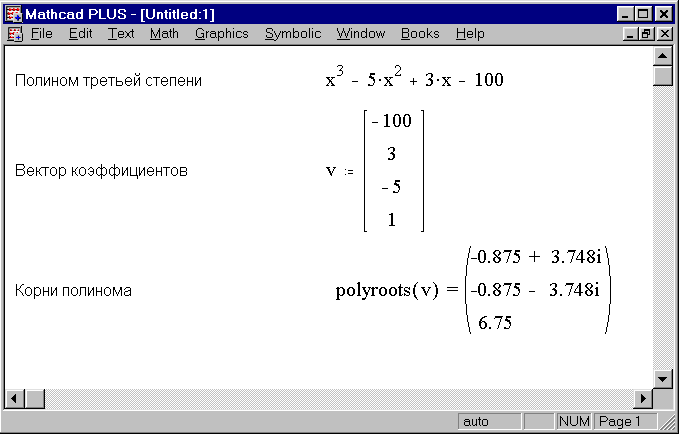
Рис. 1.2. Использование функции polyroots для поиска комплексных корней полинома
· Напечатать ключевое слово Given. Оно указывает MathCAD, что далее следует система уравнений. При написании слово Given можно использовать любой шрифт, прописные и строчные буквы. Данное слово не должно находиться в текстовой области или параграфе.
· Ниже ключевого слово Given ввести уравнения и неравенства в произвольном порядке. Правую и левую части уравнений должен отделять символ =(«жирное» = из палитры,либоиспользуя одновременно клавиши CTRL и = ).
· Введите любое выражение, которое включает функцию Find. При написании слово Find можно использовать любой шрифт, прописные и строчные буквы. Данная функция возвращает решение системы уравнений в виде одного числа или вектора, содержащего решение системы. Количество аргументов функции Find должно быть равно числу неизвестных.
Ключевое слово Given, уравнения и неравенства, а также выражение, содержащее функцию Find, называют блоком решения уравнений или решающим блоком.
На рис. 1.3 приведен пример решения одного уравнения с одним неизвестным.
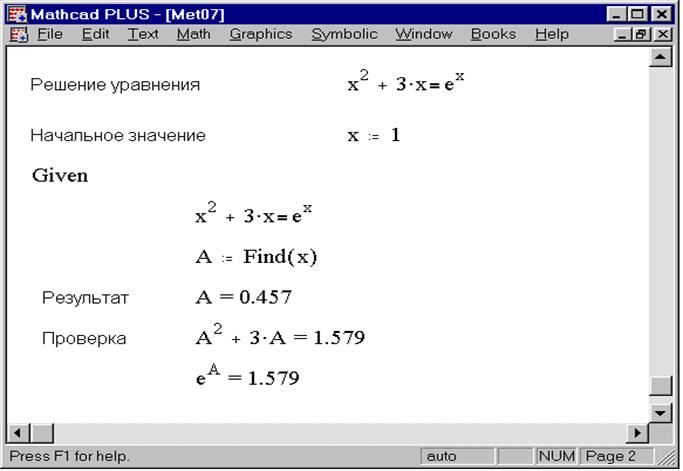
Рис. 1.3. Решающий блок для одного уравнения с одним неизвестным
На рис. 1.4 показан решающий блок, в котором использованы некоторые виды ограничений на искомое решение. Решаются два уравнения с двумя неизвестными. Функция Find возвращает результат в виде вектора с двумя компонентами.
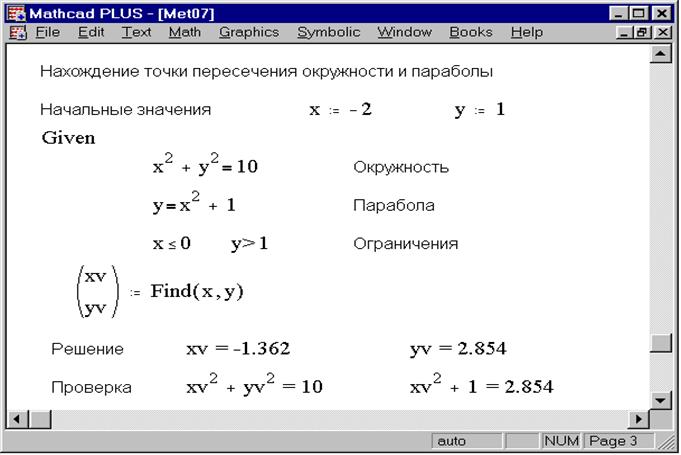
Рис. 1.4. Решающий блок для системы из двух уравнений
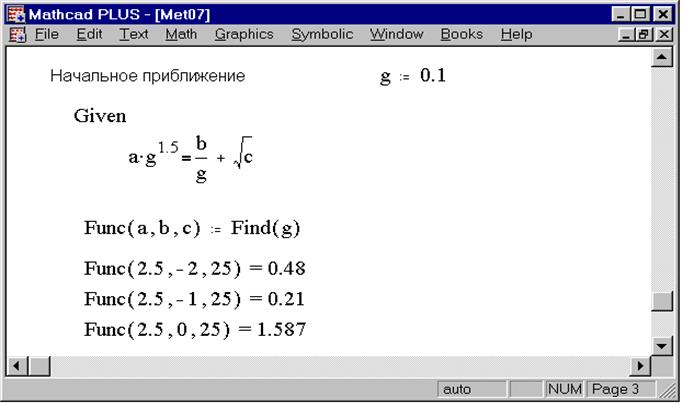
Рис. 1.5. Определение функции с использованием решающего блока
Функция Find может быть использована аналогично любой другой функции:
· Можно вывести найденное решение, напечатав выражение вида Find(x)= . Если решаются уравнения с несколькими неизвестными, то можно вывести вектор результатов в виде Find(x1,x2,x3)= .
· Можно определить переменную с использованием функция Find , для этого в конце решающего блока следует ввести выражение A:=Find(x). В данном случае переменную A можно использовать в другом месте рабочего документа, что показано на рис. 1.3. Если функция Find возвращает вектор результатов, можно ввести выражение вида A:=Find(x1,x2,x3) или как показано на рис. 1.4.
· Используя функцию Find , можно определить другую пользовательскую функцию. Для этого необходимо закончить блок решения уравнений выражением типа f(a,b,c,d):=Find(x1,x2,x3). Эта конструкция удобна в случае многократного решения системы уравнений для различных значений некоторых параметров a,b,c,d, входящих в систему уравнений. Например, на рис. 1.5 определена функция Func(a,b,c), каждый раз при выполнении которой аргументы a,b,c подставляются в блок и вычисляется результат
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.