Исследование кусочно-непрерывной функции

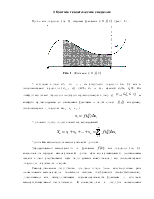
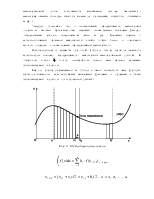
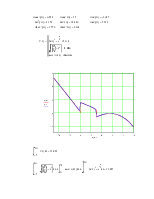
Таблица основных (глобальных) переменных приведена в таблице 2.

Таблица 2 – Глобальные переменные

4.3.2 Процедура построения вертикального меню (menu)

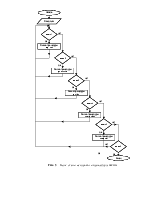
Блок-схема процедуры построения меню приведена на рис. 3.

Выбор пункта меню происходит следующим образом: на экран выводятся все пункты меню и затем первый пункт – инверсным цветом. Далее в программе идёт считывание нажатий клавиш. Если нажаты клавиши “вверх” или “вниз” происходит вывод текущего пункта меню на экран прямым цветом, затем рассчитывается новый текущий пункт меню в соответствии с нажатой клавишей, и затем выводится новый текущий пункт меню инверсным цветом. При нажатии клавиши “Enter” происходит вызов соответствующей подпрограммы в соответствии с приведенной на рис. 3 блок-схемой алгоритма.

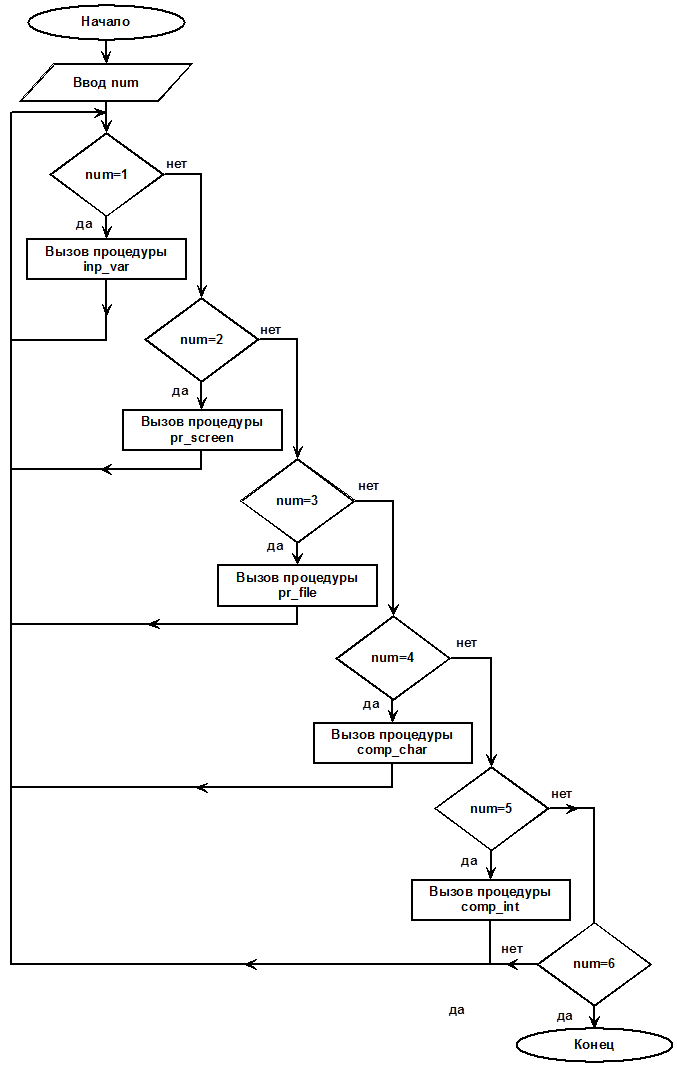
Рис. 3 – Блок-схема алгоритма процедуры menu

4.3.3 Процедура ввода входных данных (inp_var)

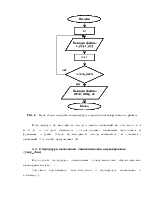
Блок-схема процедуры ввода входных данных приведена на рис. 4.

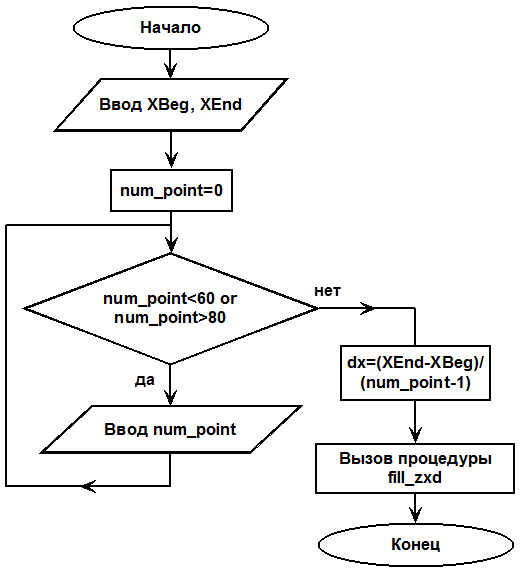
Рис. 4 – Блок-схема алгоритма процедуры ввода входных данных

В процедуре производится ввод основных входных параметров, таких как:

·  XBeg - Начальное значение X

·  XEnd - Конечное значение X

·  Num_point – Количество точек

В конце производится вызов процедуры fill_zxd, осуществляющей заполнение массива функции значениями.

4.3.4 Процедура вывода значений функции на экран (pr_screen)

Блок-схема процедуры вывода значений функции на экран приведена на рис. 5.

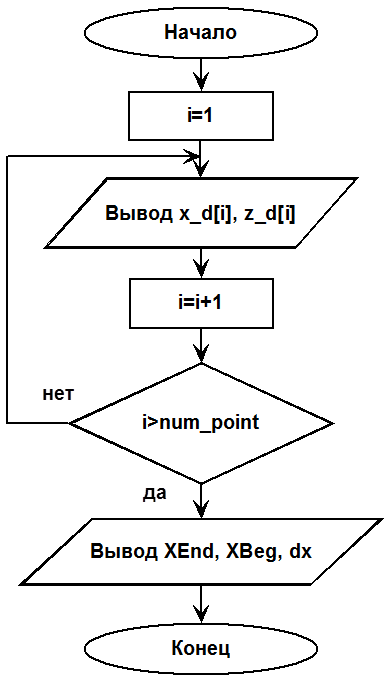
Рис. 5 – Блок-схема алгоритма процедуры вывода значений функции на экран

В процедуре производится вывод в цикле значений из массивов x_d и z_d, в которых хранятся соответственно значения аргумента и функции. Затем производится вывод начального и конечного значений X а также приращения dx.

4.3.5 Процедура вывода значений функции в файлы (pr_file)

Блок-схема процедуры вывода значений функции в файлы приведена на рис. 6.

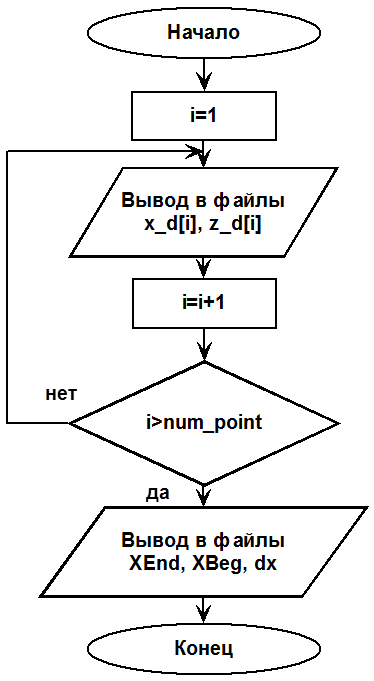
Рис. 6 – Блок-схема алгоритма процедуры вывода значений функции в файлы

В процедуре производится вывод в цикле значений из массивов x_d и z_d, в которых хранятся соответственно значения аргумента и функции, в файл. Затем производится вывод начального и конечного значений X а также приращения dx.

4.3.6 Процедура вычисления статистических характеристик (comp_char)

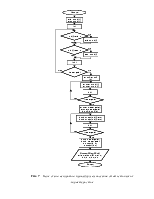
Блок-схема процедуры вычисления статистических характеристик приведена на рис. 7.

Основные переменные, используемые в процедуре, приведены в таблице 3.

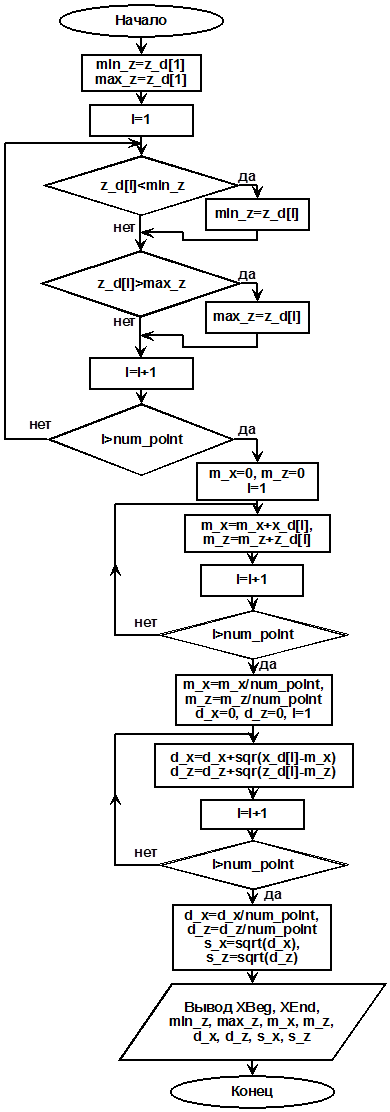
Рис. 7 – Блок-схема алгоритма процедуры вычисления статистических характеристик

Таблица 3 – Переменные процедуры comp_char

В процедуре происходит поиск максимального и минимального элементов в массиве функции z_d. После этого рассчитываются статистические характеристики, такие как математическое ожидание аргумента, математическое ожидание функции, дисперсии и среднеквадратические отклонения аргумента и функции. Затем происходит вывод рассчитанных характеристик как на экран, так и в файл.

4.3.7 Процедура вычисления интеграла функции методом прямоугольников (comp_int)

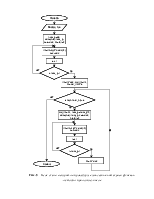
Блок-схема процедуры вычисления интеграла функции методом прямоугольников приведена на рис. 8.

Основные переменные, используемые в процедуре, приведены в таблице 4.

Таблица 4 – Переменные процедуры comp_int

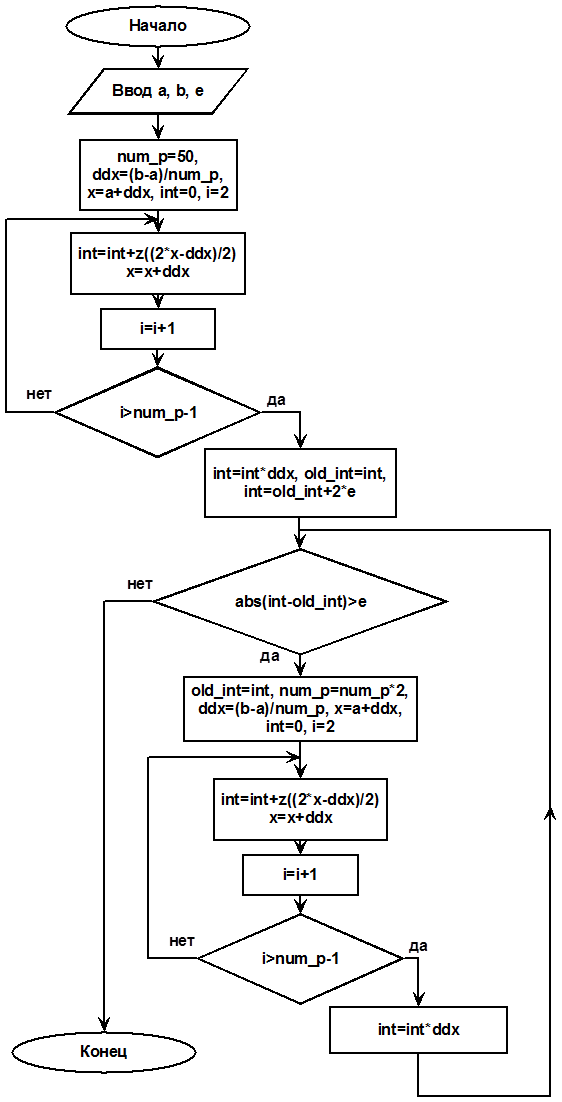
Рис. 8 – Блок-схема алгоритма процедуры вычисления интеграла функции методом прямоугольников

Изначально берется количество точек, равное 50. В соответствии с этим, заданным методом вычисляется интеграл. Затем количество точек удваивается и снова вычисляется интеграл. Процесс повторяется до тех пор, пока не будет достигнута заданная точность.

4.3.8 Процедура заполнения массива функции (fill_zxd)

Блок-схема процедуры заполнения массива функции приведена на рис. 9.

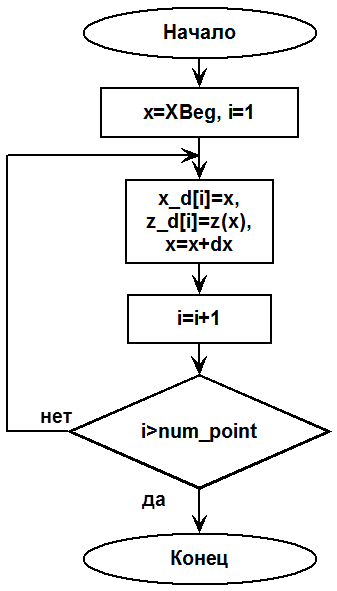
Рис. 9 – Блок-схема алгоритма процедуры заполнения массива функции