Метрология, стандартизация и сертификация: Учебное пособие. Часть 2 (Задания для выполнения практических работ по вариантам с методическими указаниями)

Федеральное государственное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

__________________________________________________________

Кафедра "Промышленный и городской транспорт"

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ

Часть 2

Учебное пособие

для студентов заочной формы обучения,

обучающихся по специальности

190701.65 «Организация перевозок и управление на транспорте»

САНКТ-ПЕТЕРБУРГ

2010

Задание 1 Практическая работа по метрологии «Обработка прямых измерений с многократными наблюдениями»

Цель работы и решаемые задачи

Изучение порядокаобработки прямых измерений с многократными наблюдениями:

- выявление и исключение грубых погрешностей (промахов) по критерию «трех сигм»;

- проверка ряда измерений на соответствие нормального закона распределения вероятностей (НЗРВ);

- построение гистограммы плотности нормального распределения вероятностей;

-  определение доверительных границ погрешности результата измерений.

 Задание

Провести обработку прямых измерений с многократными наблюдениями. Исходные данные по вариантам представлены в таблице 1 (Приложение 4).

Общие указания

При обработке измерений необходимо выявить и исключить грубые погрешности (промахи), которые могут появиться в результате неисправности средств измерений, ошибки оператора, резких изменений условий измерений. Как правило, промах сразу видны, но их наличие необходимо доказать.

Следующими этапами обработки результатов измерений являются проверка результатов измерений на соответствие НЗРВ, вычисление доверительных границы случайной погрешности результата измерения при заданной доверительной вероятности и контроль качества измерений.

Необходимо свести исходные данные в таблицу 2.3.1.

Таблица 2.3.1.

Краткие теоретические сведения и методические указания

Обнаружение и исключение случайной погрешности:

Оценка случайных погрешностей основывается на рассмотрении результатов наблюдений, результатов измерений и случайных погрешностей как случайных величин. Основой для оценки случайных погрешностей являются методы теории вероятностей и математической статистики.

Чаще всего случайные погрешности измерений подчиняются нормальному закону распределения плотности вероятности. В аналитической форме нормальный закон распределения выражается формулой:           

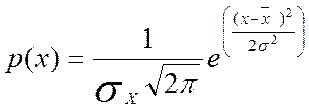                 (1.1)

где x — случайная величина;

 — среднее значение или математическое ожидание  (МО) случайной величины;

s_х — среднее квадратичекое отклонение (СКО).

Перенеся начало координат в центр распределения , и откладывая по оси абсцисс погрешность ∆x=x-, получим кривую нормального распределения погрешностей (рис. 1.1):

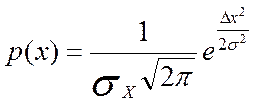                           (1.2)

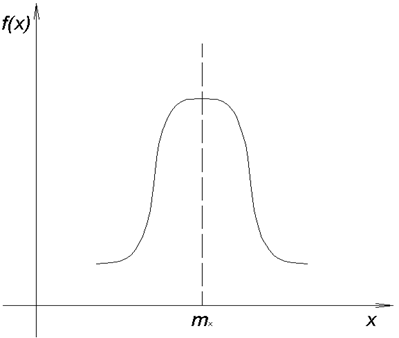
Рисунок 1.1 Кривая нормального распределения погрешностей

Для группы из n наблюдений (т.е. для дифференциального закона), распределённых по нормальному закону.

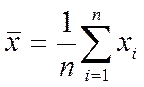               МО                        (1.3)

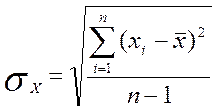   СКО                          (1.4)

Свойства нормального распределения:

1.  Кривая нормального распределения погрешностей симметрична относительно оси ординат (т.е. погрешности, одинаковые по величине, но противоположные по знаку, имеют одинаковую плотность вероятностей, т.е. при большом числе наблюдений встречаются одинаково часто)

2.  МО случайной погрешности равно нулю.

3.  Из характера кривой следует, что малые погрешности будут встречаться чаще, чем большие.

4.  Если сравнить между собой кривые нормального распределения с различными СКО, можно убедиться, что чем меньше СКО, тем меньше рассеяние результатов наблюдений и тем больше вероятность того, что большинство случайных погрешностей в них будет мало (рис 1.2).

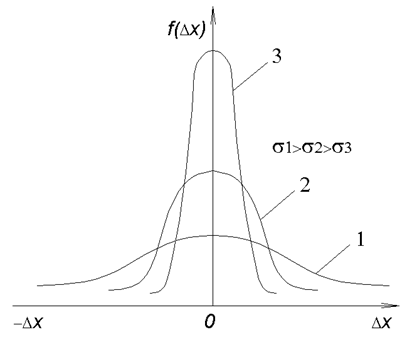
Рисунок 1.2 Зависимость СКО от рассеяния результатов наблюдений

Качество измерений тем выше, чем меньше СКО случайный погрешностей.

Интервал с границей ±Dx(P) называется доверительным интервалом случайной погрешности, а соответствующая ему вероятность — доверительной вероятностью. Принято границы доверительного интервала указывать симметричными относительно результата измерения.

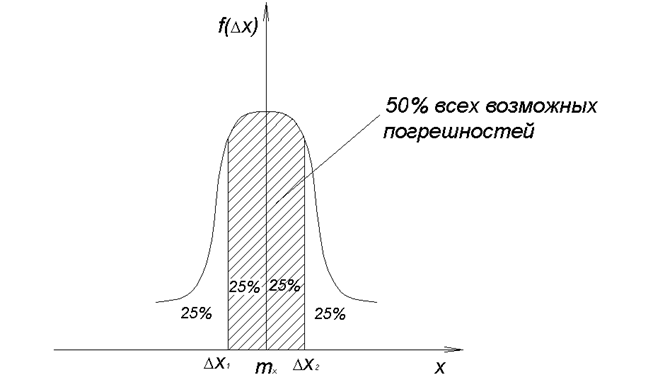
Рисунок 1.3 Интервальная оценка случайной погрешности.

Доверительные границы случайной погрешности Dx(P), соответствующие доверительной вероятности Р (таблица 2.4.1), находят по формуле:

Dx(P)=ts_х,                                                (1.5)

где t — коэффициент, зависящий от Р формы закона распределения