Расчет привода червячного двухступенчатого редуктора

Ориентировочно диаметр среднего участка вала определяется из условий прочности при кручении в случае пониженных допускаемых напряжений: ,  (мм).

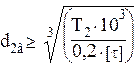                                                                              (4.13)

После подстановки получае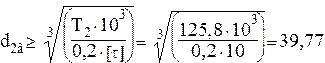м:

   мм          

Назначаем   мм - посадочный диаметр колеса;

Принимаем   вал ступенчатой формы, диаметры участков: (рис. 4.2)

 мм = 40-5=35 мм - посадочный диаметр подшипника;  - посадочный диаметр колеса

 = 52,8 мм  - диаметр впадин зубьев червяка

На основании эскизного проектирования принимаем расстояние между опорами:    = 345 мм

 = ;  =

Выписываем все силы, действующие на вал:

 = ;   = ;     = 3494 Н;               = ;      = ;       = 1573 Н;       

Для валов расчет на сопротивление усталости является основным, а расчет на статическую прочность выполняется как проверочный.

Определим  опорные реакции.        Изображаем вал как балку на двух опорах

Найдём  реакции в горизонтальной плоскости

;             

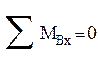имеем:

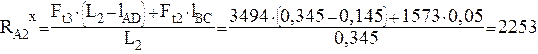   Н                                  (4.14)

;             

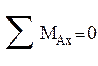имеем:

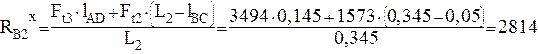   Н                                  (4.15)

Найдём  реакции в вертикальной плоскости

;             

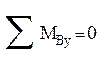имеем:

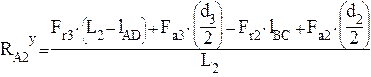 ,  Н                                                  (4.16)

Имеем:

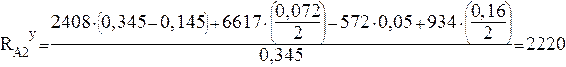   Н            

;             

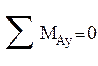имеем:

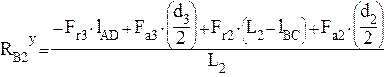 ,  Н                                              (4.17)

Подставляя  значения переменных величин получаем:

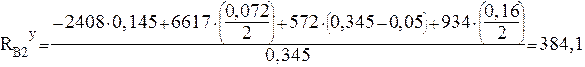   Н        

Определим  суммарные реакции:

  Н

  Н

Определим  изгибающие моменты

;             ;                ;       ;          

;             ;                ;              ;      ;    ;          

Рассчитаем  эквивалентный и суммарный изгибающий моменты в опасном сечении D:

 

 

Рассчитаем необходимый диаметр вала в опасном сечении D ,  (мм).

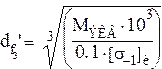                                                                          (4.18)

где        = 55 МПа - допускаемое напряжение при изгибе для обеспечения не только прочности, но и достаточной жёсткости вала.

После подстановки получае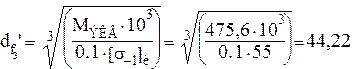м:

   мм    

Так как необходимый диаметр меньше  изначально принятого  = 52,8 мм, то оставляем ранее принятые размеры вала.

рассчитаем момент сопротивления вала кручению

 =                                                                                   (4.19)

имеем:

 

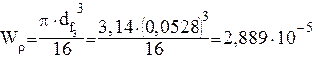
Момент сопротивления вала изгибу рассчитывается по формуле

W =                                                                                   (4.20)

подставим    значения     имеем:

 

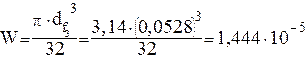
Амплитуду и среднее значение касательных напряжений от нулевого цикла подсчитывается по выражению

   =                                                                               (4.21)

после подстановки      получим:

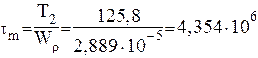    Па = 4,354  МПа

Амплитуду цикла нормальных напряжений подсчитывается по выражению

 =                                                                                   (4.22)

подставим    значения     получим:

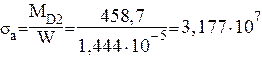  Па = 31,77  МПа

Найдём коэффициент запаса прочности по касательным напряжениям

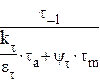 =                                                                           (4.23)

где        = 1.7   - коэффициент концентрации касательных напряжений;

 = 0,69   - значение масштабного фактора ;

 = 0.15   - коэффициент, характеризующий чувствительность материала к асимметрии цикла касательных напряжений;

 =  = 230  МПа - предел выносливости материала вала при кручении;

получим:

 

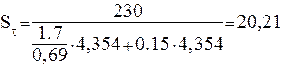
Коэффициент запаса прочности по нормальным напряжениям найдём по формуле

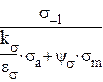 =                                                                           (4.24)

где        = 2.3   - коэффициент концентрации нормальных напряжений;

 = 0,69   - значение масштабного фактора ;

 = 0.25   - коэффициент, характеризующий чувствительность материала к асимметрии цикла нормальных напряжений;

 = 0;

  МПа - предел выносливости материала вала при изгибе;

имеем:

 

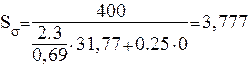
Рассчитаем результирующий коэффициент запаса прочности

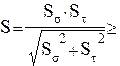
                                                                           (4.25)

где        = 2,5...4 - требуемый запас прочности для обеспечения прочности и жёсткости.

Отсюда имеем:

              

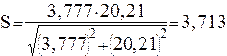
Условие (4.25) выполнено.

4.3. Расчёт 3 - го вала

Принимаем   материал вала - Сталь 45,  МПа.

Ориентировочно диаметр выходного конца вала определяется из условий прочности при кручении в случае пониженных допускаемых напряжений:

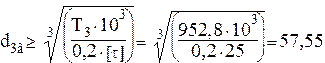   мм                                                      (4.26)

Назначаем   мм

Принимаем   вал ступенчатой формы (рис. 4.3)

 =   мм = 60+5 = 65 мм -  диаметр уплотнения;

 =   мм = 65+5 = 70 мм - посадочный диаметр подшипника;

 =  мм = 70+5 = 75 мм - посадочный диаметр колеса принимаем расстояние между опорами:

                                                                            (4.27)

где        = 8...15 мм - зазор между зубчатыми колёсами и внутренними стенками корпуса редуктора ;

 = 55...95 мм - ширина стенки корпуса в месте установки подшипников ;

 мм.

Подставим значения                = 230 мм

Принимаем f =  = 115 мм - ;  =

Выписываем все силы, действующие на вал:

   Н;             = ;   = ;     = 6617 Н;             

Для валов расчет на сопротивление усталости является основным, а расчет на статическую прочность выполняется как проверочный.

Определим  опорные реакции.        Изображаем вал как балку на двух опорах

Определим  реакции в горизонтальной плоскости

;             

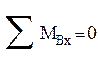имеем:

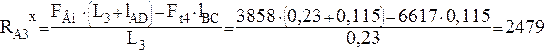   Н                                  (4.28)

;             

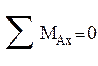имеем:

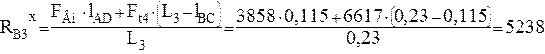   Н                                  (4.29)

Подсчитаем  реакции в вертикальной плоскости

;             

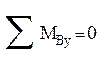имеем:

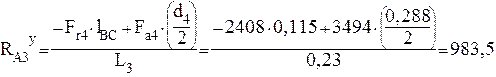   Н                                      (4.30)

;             

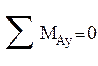имеем:

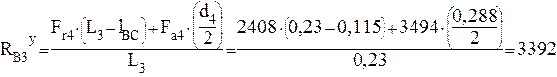   Н                              (4.31)

Рассчитаем  суммарные реакции:

  Н

  Н

Подсчитаем  изгибающие моменты

;             ;                ;     ;          

;           ;             ;                ;  ;          

Определим  эквивалентный и суммарный изгибающий моменты в опасном сечении C:

 

 

Рассчитаем необходимый диаметр вала в опасном сечении C

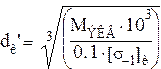 ,  мм                                                                      (4.32)

где        = 55 МПа - допускаемое напряжение при изгибе для обеспечения не только прочности, но и достаточной жёсткости вала.

Подставляя  значения переменных получае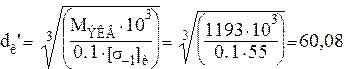м:

   мм      

Так как необходимый диаметр меньше  изначально принятого  = 75 мм, то оставляем ранее принятые размеры вала.

Момент сопротивления вала кручению рассчитывают  по формуле

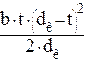 =  -                                                                       (4.33)

где       b - ширина шпонки, м;

t - глубина впадины вала, м.

для диаметра  = 75 мм имеем  шпонку  сечения 20  12  ;

подставляя    значения     имеем:

 -   -    

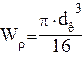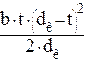
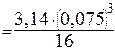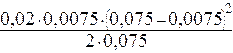
Определим момент сопротивления вала изгибу

W =  -  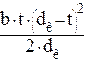                                                                     (4.34)

получим:

 -   -    

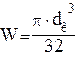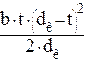
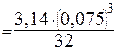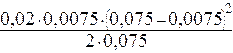
Амплитуду и среднее значение касательных напряжений от нулевого цикла определим по формуле

   =                                                                               (4.35)

после подстановки    значений переменных   получим:

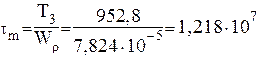    Па = 12,18  МПа

Амплитуду цикла нормальных напряжений находится по выражению

 =                                                                                   (4.36)

подставим    значения переменных   получим:

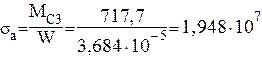  Па = 19,48  МПа

Коэффициент запаса прочности по касательным напряжениям находится по выражению

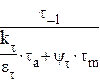 =                                                                           (4.37)

где        = 1.5   - коэффициент концентрации касательных напряжений;

 = 0,64   - значение масштабного фактора ;

 = 0.10   - коэффициент, характеризующий чувствительность материала к асимметрии цикла касательных напряжений;

 =  = 140  МПа - предел выносливости материала вала при кручении;

после подстановки      имеем:

 

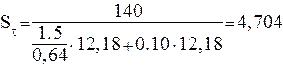
Коэффициент запаса прочности по нормальным напряжениям найдём