Изучение зависимости температуры нити лампы накаливания от потребляемой мощности

Петербургский Государственный Университет Путей Сообщения

Кафедра физики

Электротехническая лаборатория

Лабораторная работа №201-6

Изучение зависимости температуры нити лампы накаливания от потребляемой мощности

Выполнил студент

Гр РТС-312

Болгов Егор

Проверил __________________

Санкт – Петербург

2004 г.

Оглавление:

1.    Теоретические данные.. 3

2.    Цель работы... 4

3.    Порядок выполнения работы... 5

4.    Таблицы... 6

1.  Теоретические данные

Ток, текущий по нити лампы накаливания, нагревает проводник и заставляет излучать.

В установившемся режиме вся подводимая к проводнику мощность

P=UI (1)

Идет на излучение.

Мощность, излучаемая единицей поверхности металла, который нагрет до абсолютной температуры T, определяется соотношением:

(2)

,где σ = 5,67*10^-8 Вт/(м²*К⁴) – постоянная Стефана – Больцмана. К=0,30 – коэффициент поглощения вольфрама (он равен доле падающего излучения, которая поглощается нагретым телом).

Если нить лампочки – цилиндрический проводник с диаметром D и длинной L, то величина излучающей поверхности равна (πDL), а мощность, излучаемая лампочкой, определяется выражением:

 (3)

из (1) и (3) вытекает

Для определения абсолютной температуры T воспользуемся формулой зависимости сопротивления металлических проводников от температуры,

отсюда

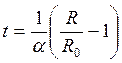
, где R₀ – сопротивление проводника при 0⁰С (значение R₀ дано на рабочем месте), t – температура по шкале Цельсия, α – температурный коэффициент сопротивления (он равен относительному увеличению сопротивления проводника при нагревании его на 1 градус).

В общем случае α зависит от температуры. В ограниченном диапазоне температур (до 500⁰ С) этой зависимостью можно пренебречь и считать α=const(t).

Для чистых металлов α≈1/273. В настоящей работе в качестве проводника используется нить лампочки накаливания из вольфрама с температурным коэффициентом α=4.8*10^-3.

По закону Ома сопротивление лампочки R=U/I. Таким образом для температуры T=273+t получим выражение:

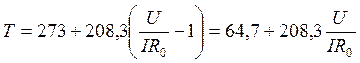
Сопротивление вольфрамовой нити диаметром D и длинной L при 0⁰С равно:

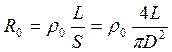
Удельное сопротивление при 0⁰С для вольфрама имеет значение ρ₀=5,5*10^-8 Ом.

Геометрические размеры проводника найдем, используя два соотношения: формулу для сопротивления R₀ однородного проводника и выражение для мощности, излучаемой поверхностью нагретой нити лампочки.

2.  Цель работы

Получение вольт-амперной характеристики проводника, определение по ней зависимости T(P),оценка неэлектрических параметров проводника – длины и диаметра – по результатам электрических измерений I(U) и заданному значению R₀.

3.  Порядок выполнения работы

1.  Включить выпрямитель в сеть, ключ К1 перевести в верхнее положение. Потенциометром П1 установить по вольтметру напряжение 1-2 В.

2.  Изучаемый проводник (лампочка) включен последовательно с потенциометром П2. Вывести П2 до отказа вправо, при этом увеличивается ток по амперметру А.

3.  С помощью П1 подобрать напряжение U, при котором ток в цепи будет максимальным. Значения напряжения U и тока занести в таблицу. Разбить диапазон 0 – U на 10-15 интервалов и снять зависимость I(U). Результат занести в таблицу. Построить график.

4.  Вычислить сопротивление проводника R=U/I. Результат занести в таблицу, построить график зависимости R(U).

5.  Во всех измеренных точках вычислить температуру проводника по кельвину. Результат занести в таблицу.

6.  Вычислить мощность P и корень четвертой степени из мощности. Занести в таблицу. Построить график .

7.  Выбрать линейный участок на графике  и определить угловой коэффициент прямой.

8.  Оценить длину и диаметр проводника.

9.  Вычислить погрешности.

4.  Таблицы