Исследование временных и частотных характеристик детерминированных сигналов (ТПС), страница 3

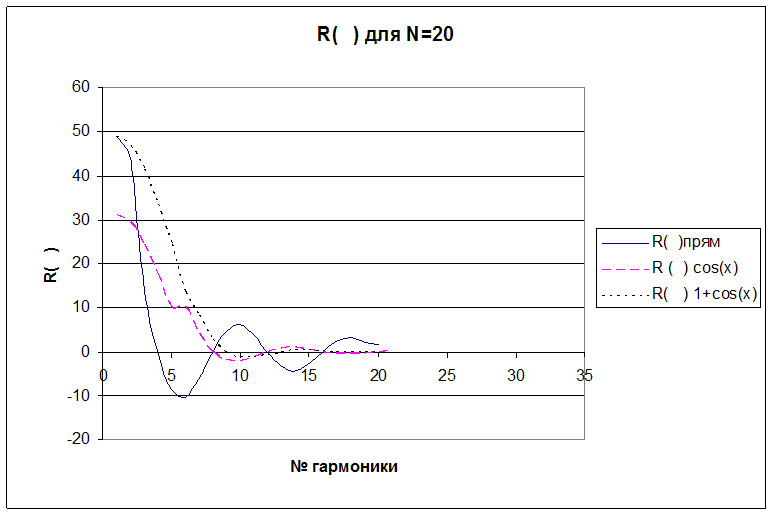
3. Выводы

Анализируя графики спектра напряжения для различных сигналов, можно сказать, что при резком ограничении формы сигнала (как в случае с прямоугольным) его спектр похож на функцию sin(x)/x, а если в форме сигнала нет разрывов ни первого ни второго рода, то его спектр подобен форме сигнала.

Графики спектров мощности получаются из спектров напряжения путем возведения этих спектров в квадрат, они показывают распределение энергии в частотной области. По спектру мощности мы не сможем восстановить сигнал, так как в нем нет информации о фазовом сдвиге сигналов.

Смотря на временные характеристики сигналов можно сказать, что чем больше гармоник мы берем для восстановления формы сигнала, тем более похожа получается его форма по отношению к идеальной. Также мы видим, что «хуже» восстанавливается сигнал прямоугольной формы, из-за того, что в его форме присутствуют разрывы первого рода.

Функция автокорреляции характеризует взаимозависимость между значениями одного и того же сигнала, сдвинутыми на время τ. При τ = 0 она характеризует энергию сигнала. Анализируя ее графики  можно сказать, что эта функция четная (т.к. получена из четной функции спектра мощности) и монотонна убывающая. Для сигнала прямоугольный формы она имеет ярко выраженный линейный характер.