Временная вход-выходная последовательность

ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ

Кафедра «Автоматика и телемеханика на железных дорогах»

Курсовая работа по ТДУ

Вариант №7

Выполнил ст. гр. АР-309:

Кулешов Ю. В.

Проверил:

Санкт – Петербург

2005г.

Задание

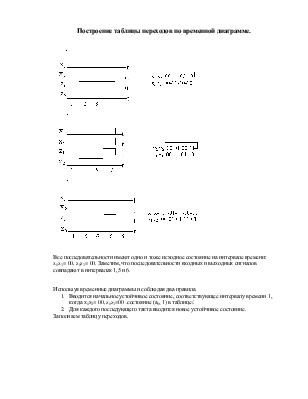
Курсовая работа задана с помощью временной вход-выходной последовательности. Она имеет следующий вид:

Построение таблицы переходов по временной диаграмме.

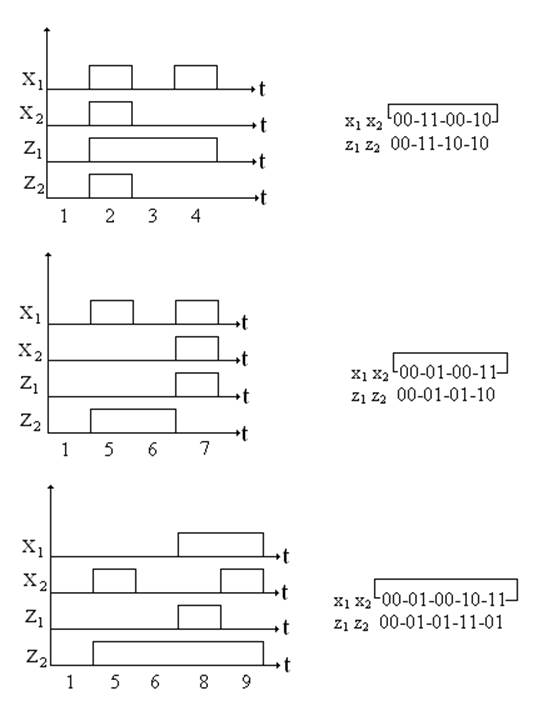
Все последовательности имеют одно и тоже исходное состояние на интервале времени: x₁x₂= 00, z₁z₂= 00. Заметим, что последовательности входных и выходных сигналов совпадают в интервалах 1,5 и 6.

Используя временные диаграммы и соблюдая два правила.

1.  Вводится начальное устойчивое состояние, соответствующее интервалу времени 1, когда х₁х₂= 00, z₁z₂=00 .состояние (а₁, 1) в таблице/.

2.  Для каждого последующего такта вводится новое устойчивое состояние.

Заполняем таблицу переходов.

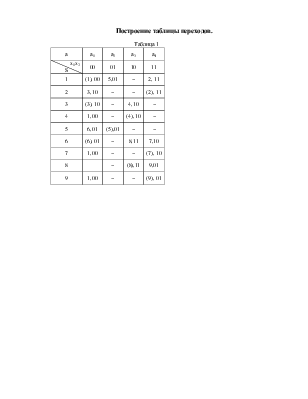
Построение таблицы переходов.

Таблица 1

Минимизация таблицы переходов.

Критерием оптимальности полученной ТП является минимум числа ее строк, так как от числа строк зависит число реле, необходимое для построения схемы. Поэтому после построения первичной ТП необходимо осуществить минимизацию числа строк. Эта минимизация возможна вследствие наличия в ТП безразличных состояний.

Две строки ТП называются совместимыми, если они имеют непротиворечивое размещение цифр, т.е. в одном столбце этих строк записаны одинаковые цифры или в одной строке записана цифра, а в другой – знак безразличного состояния.

Общая идея минимизации числа строк ТП заключается в нахождении всех максимальных подмножеств совместных строк и определении наилучшего варианта объединения строк.

Находим множества Е_j – множества строк, в которых в столбце поставлено состояние j или знак безразличного состояния:

Столбец а₁:                                                     

Е₁=(1, 4, 7, 8, 9)                                                

Е₃=(2, 3, 8)                              

Е₆=(5, 6,8)                            

Столбец а₃:                                                    Столбец а₄:

Е₄=(1, 2, 3, 4, 5, 7, 9)                                    Е₂=(1, 2, 3, 4, 5)

Е₈=(1, 2, 5, 6, 7, 8, 9)                                    Е₇=(3, 4, 5, 6, 7)

Е₉=(3, 4, 5, 8, 9)

Столбец а₂ имеет одно устойчивое состояние, множества не составляются.

Найдем множества, строки  которых не содержат противоречивых цифр:

Е₁₄₂= (1, 4) – А                                             Е₃₈₂= (2)

Е₁₄₇= (4, 7) – В                                              Е₃₈₇= (0)

Е₁₄₉= (4, 9) – С                                              Е₃₆₉= (8)

Е₁₈₂= (1)                                                        Е₆₄₂= (5)

Е₁₈₇= (7)                                                        Е₆₄₇= (5)

Е₁₈₉= (8, 9) – D                                             Е₆₄₉= (5)

Е₃₄₂= (2, 3) – E                                              Е₆₈₂= (5)

Е₃₄₇= (3)                                                        Е₆₈₇= (5, 6) - F

Е₃₄₉= (3)                                                        Е₆₈₉= (5, 8) - G

Из полученных множеств исключаются те, которые полностью входят в другое множество. Оставшиеся множества являются максимальными подмножествами совместных строк. Обозначим их латинскими буквами:

Е₁₄₂= (1, 4) – А                                             Е₃₄₂= (2, 3) – E

Е₁₄₇= (4, 7) – В                                              Е₆₈₇= (5, 6) - F

Е₁₄₉= (4, 9) – С                                              Е₆₈₉= (5, 8) - G

Е₁₈₉= (8, 9) – D

Составляем таблицу покрытий. Ее столбцы соответствуют множествам А, В,…..,G, а строки первичной ТП. На пересечении строки и столбца знак “+”, если данная строка ТП входит в данное  подмножество совместимых строк.

Решается задача покрытия :находится минимальное множество W множеств А, В,….,G такое, что каждая строка входит хотя бы в одно из них.

Для этого составляются алгебраическое выражение Q типа конъюнкция дизъюнкций. Число дизъюнкций равно числу строк. Каждая дизъюнкция образуется как дизъюнкция тех столбцов, в которых стоит метка “+” в данной строке.

Таблица 2

Для (таблицы 2) имеем:

Q=A E E (A+B+C) (F+G) F B (D+G) (C+D);

При вычислении используются правило повторения

AA = A;

и правила поглощения

A+ Ax = A;

A(A+ x) = A, где x – любое выражение.

В итоге получаем:

Q = ABDEF+ ABCEFG;

Множество W задается любой из конъюнкций минимального ранга выражения Q. В данном случае такая конъюнкция одна:

W= A B D E F = (1, 4) (4, 7) (8, 9) (2, 3) (5, 6);

Множество W преобразуется в множество W’ такое, что каждая строка первичной ТП входит только в одно из его подмножеств:

W’= (1,) (4, 7) (8, 9) (2, 3) (5, 6);

Производится объединение строк с использованием указанного выше правила.

Таблица 3

Производится перенумерация строк, и получаем минимизированную ТП (таблица 4). Принцип перенумерации заключается в присвоении каждой строке (таблицы 3) порядкового номера.

Таблица 4

Таким образом, подмножествам (1,) (2, 3)  (4, 7) (5, 6) (8, 9) присвоены порядковые номера соответственно 1, 2, 3, 4, 5. Затем цифры  состояний внутри клеток (таблицы 3) заменяются цифрами, присвоенными тем подмножествам, в которые эти состояния входят.

В ячейки с безразличными состояниями, ставим  состояния удобные