РЕЗУЛЬТАТЫ
1. Проверка правильности вычислений.
Воспользовавшись формулами (1)-(4):
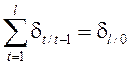 ,
, ![]() ; (1)
; (1)
![]() ; (2)
; (2)
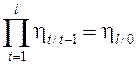 ,
, ![]() ; (3)
; (3)
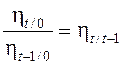 . (4)
. (4)
убедились в правильности нахождения абсолютных приростов: базисного и цепного; темпов роста: базисного и цепного.
2. Определение типа экономического развития.
Тип экономического развития – Тип 2. Поскольку на графике абсолютного базисного прироста наблюдается по большей части увеличение значений прироста, поэтому и считаем, что у нас рост увеличивающийся.
3. Анализ подобранных функций тренда для динамического ряда:
За математическую
модель тренда мы принимаем некоторое уравнение ![]() , где
фактические уровни
, где
фактические уровни ![]() мы заменяем теоретические, причем
эти уровни рассматриваются как функции времени.
мы заменяем теоретические, причем
эти уровни рассматриваются как функции времени.
При этом
каждый фактический уровень ![]() рассматривается как
сумма двух составляющих:
рассматривается как
сумма двух составляющих: ![]() , где
, где ![]() – систематическая составляющая, отражающая
тренд и выраженная определенным уравнением, а
– систематическая составляющая, отражающая
тренд и выраженная определенным уравнением, а ![]() –
случайная величина, вызывающая колебания уровней вокруг тренда.
–
случайная величина, вызывающая колебания уровней вокруг тренда.
По данному динамическому ряду были построены 4 тренда со следующими полученными уравнениями:
Логарифмический тренд y = 1,3105Ln(x) + 105,55
![]() = 0,1299
= 0,1299
Полиномиальный тренд y
= -0,0136![]() + 0,4431x + 105,77
+ 0,4431x + 105,77
![]() = 0,0974
= 0,0974
Экспоненциальный
тренд y = 107,19![]()
![]() = 0,061
= 0,061
Линейный тренд y = 0,1036x + 107,24
![]() = 0,0589
= 0,0589
Степенной ряд (y =
105,53![]() ;
;![]() = 0,1328) практически
совпал с логарифмическим, поэтому мы его не рассматривали.
= 0,1328) практически
совпал с логарифмическим, поэтому мы его не рассматривали.
Судя по
величине достоверности аппроксимации, которая по своему качеству в хорошей
аппроксимации должна стремиться к единице, наиболее подходящим трендом для
нашего ряда является логарифмический ряд, где ![]() =0,1299.
=0,1299.
Если же в качестве оценивателя брать расстояние от тренда до исходного графика, то получаем следующие цифры:
Логарифмический тренд: R=13,46658911
Полиномиальный тренд: R=13,71266114
Экспоненциальный тренд: R=13,741447
Линейный тренд: R=13,7273394
И снова мы убедились в том, что логарифмический тренд более лучше аппроксимирует исходную модель: расстояние от тренда до модели из всех рассмотренный трендов – минимальное.
С геометрической точки зрения, график логарифмического тренда является возрастающей функцией, как видно из следующего графика:
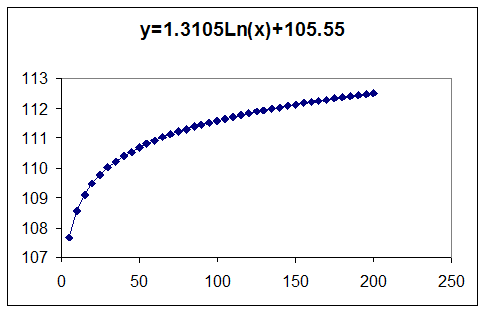
А в пункте 2 мы установили, что тип экономического развития -2: увеличивающийся рост; характеризуется увеличивающимся абсолютным приростом.
Таким образом,
если предположить, что выявленная закономерность возрастания развития будет
устойчива и сохраняться в будущем, то есть, что условия, в которых происходили
изучаемые явления в определенном периоде в прошлом, стабильны и
предположительно не изменяться в ближайшем будущем, на которое экстраполируется
ряд, то найденное уравнение логарифмического тренда вполне может использоваться
для прогнозирования с учетом некоторой случайно величины ![]() , которая , по возможности, будет
корректировать спрогнозированные результаты.
, которая , по возможности, будет
корректировать спрогнозированные результаты.
4. Сравнение качества аппроксимации наблюдений по методам скользящего среднего и аналитического выравнивания.
Как отмечалось выше, в качестве аналитического выравнивания мы определили для себя логарифмический тренд
Если в
качестве оценивателя качества аппроксимации между методом скользящего среднего
и логарифмического тренда брать величину ![]() , то
есть расстояние от спрогнозированного ряда до исходного ряда, то в этом случае
получаем такие цифры:
, то
есть расстояние от спрогнозированного ряда до исходного ряда, то в этом случае
получаем такие цифры:
Для метода скользящего среднего: R=6.4443
Для логарифмического тренда: R=13.4667
С этой точки зрения получаем, что метод скользящего среднего более близко аппроксимирирует исходный ряд. В чем заключается его плюс, но минус в том, что этот метод также продолжает отражать существенные скачки ряда, в отличии от логарифмического тренда, который компенсирует эти скачки каким то более усредненным значением.
Таким образом, для того, чтобы получить более гибкий и приближенный к истинным значениям ряд, но по-прежнему отражающего скачки значений ( если таковые есть) лучше использовать метод скользящего среднего. Если же требуется более идеализированная модель, с целью дальнейшего прогноза, то использовать лучше логарифмический тренд.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.