Теория игр

Здесь первое слагаемое по предположению не превосходит 2р_n+1, а второе больше 2р_n+1. Поэтому  .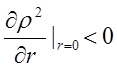

Отсюда следует, что для r, достаточно близких к нулю

Но это противоречит выбору z. Следовательно для любых у из В

15) Теорема о минимаксе.

Для любой функции F(x,y), определенной на произвольном декартовом произведении , имеет место неравенство

        (1)

Отсюда следует, что .

Нижний выигрыш 1 не может превышать верхнего проигрыша игрока 2.

Теоремао минимаксе утверждает, что .

Эта важнейшая теорема доказана многими способами. Используем доказательство фон Неймана и Моргенштерна. Для доказательства теоремы рассмотрим сначала две леммы.

Лемма 2. Пусть А = {a_ij}, матрица . Тогда справедливо либо утверждение 1, либо 2.

1.  точка `О (в m – мерном пространстве) содержится в выпуклой оболочке m + n точек

………………

и

,

,

………………

.

2.  существуют числа х₁, … , х_m, удовлетворяющие условиям

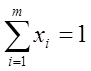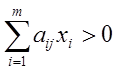 , , , j = 1, …, n.

Доказательство.

Предположим, что 1 не верно. Т.е. точка`О не содержится в выпуклой оболочке.

На основании Леммы1 существуют такие числа р₁, …, р_m+1, что

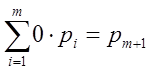 Þ  p_m+1 = 0 и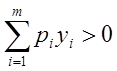 

для всех`у в указанном выпуклом множестве. В частности это выполняется, если`у является любым из m+n векторов a_j, e_i. Поэтому

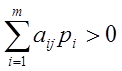для 

 для 

Т.к. , получаем  , и можно положить

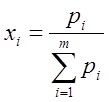
Следовательно, , , .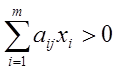

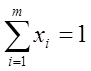Лемма доказана .

16) Доказательство теоремы о минимаксе.(V₁=V₂)

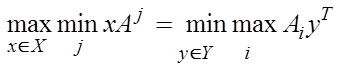, где A^j – столбец, а A_i – строка.

Пусть A – матричная пара. По лемме 2 имеет место либо утверждение (1), либо утверждение (2).

Если верно (1), то `0 является выпуклой линейной комбинацией m+n векторов. Поэтому существуют такие S₁,…, S_m+n, что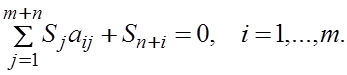

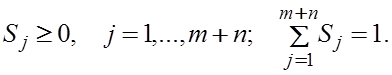
Если бы все числа S₁,…, S_n были равны нулю, то`0 оказывался бы выпуклой линейной комбинацией m единичных векторов e₁, e₂,…, e_m, что, очевидно, невозможно, т.к. они линейно независимы. Следовательно, по крайне мере одно из чисел S₁,…, S_n положительно и 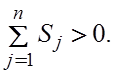 Тогда можно положить 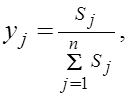и мы получаем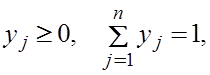  

Значит 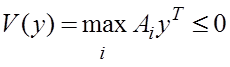 и

Предположим теперь, что верно утверждение (2).

.

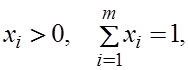
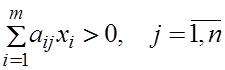Тогда, 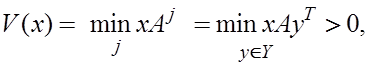так что

Следовательно, неравенство  не может иметь ??????????????

Предположим теперь, что мы изменили игру А, заменив её на игру B={b_ij}, где . Ясно, что для любых x, y 

Поэтому  

Т.к. неравенство  не может иметь места, то неравенство  также не выполняется. Но k – произвольно. Значит, неравенство, то , что и требовалось доказать.

Т.о., мы видим, что при использовании смешанных стратегий нижний выигрыш игрока 1 в точности равен верхнему проигрышу игрока 2. Общая величина V этих двух чисел называется значением игры.

Мы видим, что стратегия x, удовлетворяющая условию

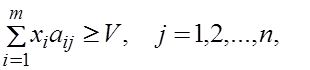                                                                                                                                              (2)

является оптимальной для игрока 1 в том смысле, что не существует стратегии, которая дала бы ему больший ожидаемый выигрыш, чем V, против каждой стратегии игрока 2.

Обратно, если y удовлетворяет условию

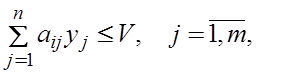                                                                                                                                              (5)

то y является оптимальной для игрока 2 в том же смысле.

Далее, очевидно, что xAy^т = V, т.к. если бы правая часть этого равенства была меньше левой, то это противоречило бы (5), а если бы она была больше левой – это противоречило бы (4). Следовательно, оптимальнее стратегии x и y являются также оптимальными одна против другой, а также против любой иной оптимальной стратегии.

Будем называть любую пару оптимальных стратегий (x,y) – решением игры.

17) Вычисление оптимальных стратегий.

Теорема о минимаксе гарантирует, что каждая антагонистическая игра имеет оптимальные стратегии. Она даёт существование, но не определяет, как искать эти оптимальные стратегии.

1.  Простейшим является тот случай, когда существует седловая точка, т.е.

когда существует элемент a_ij, являющийся максимальным в своём столбце и минимальным в своёй строке. Тогда чистые стратегии i и j (или, что равносильно, смешанные стратегии x и y, для которых x_i=1, y_j=1, а все остальные компоненты равны нулю) будут оптимальными стратегии для игроков 1 и 2 соответственно.

2.  Доминирование. Пусть дана матрица A. Будем говорить, что i-ая строка доминирует k-ую строку, если  и   по крайней мере для одного j.

Аналогично, будем говорить, что j-ый столбец доминирует l-ый столбец, если   и  по крайней мере для одного i.

Короче говоря, одна чистая стратегия (представленная своей строкой или столбцом) доминирует другую чистую стратегию, если выбор первой (доминирующей) стратегии по крайней мере не хуже выбора второй (доминируемой) стратегии, а в некоторых случаях и лучше.

Отсюда следует, что игрок всегда может обойтись без доминируемых стратегий и использовать только недоминируемые стратегии. 

Теорема.(Без доказательства)

Пусть А – матричная игра, и пусть строки i_1, i_2,…, i_k матрицы доминируются. Тогда игрок 1 имеет такую оптимальную стратегию x, что ; кроме того, любая оптимальная стратегия для игры, получающейся в результате удаления доминируемых строк, будет также оптимальной стратегией для первоначальной игры.

Аналогичная теорема справедлива и для доминирования столбцов. Общий результат этих теорем состоит в том, что все доминируемые строки и столбцы могут быть отброшены, а это позволяет иметь дело с меньшей матрицей.

Пример.

Рассмотрим игру с  матрицей 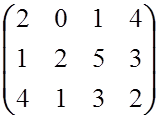. Второй столбец доминирует 4-ый. Следовательно, игрок 2 никогда не будет использовать свою 4-ую стратегию. Поэтому на неё можно не обращать внимания и рассматривать матрицу