Структуры данных и алгоритмов, используемых в МКЭ

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

кафедра прикладной математики

Лабораторная работа №2

по дисциплине:

«Метод конечных элементов»

Факультет:      ПМиИ

Группа:            ПМ-05, ПМ-06

Студенты:        Самоволик Н.Ю.

Шатрова А.А.

Преподаватели:   Чернышев А.В.

Петров Р.В.

Новосибирск, 2004

Цель работы

Изучение структур данных и алгоритмов, используемых в МКЭ, изучение приёмов вычисления локальных матриц с использованием барицентрических координат.

Результаты

Уравнени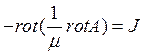е: ,  где

 магнитная индукция,

вектор-потенциал,

магнитная проницаемость среды.

Все необходимые исследования будем производить в следующей области:

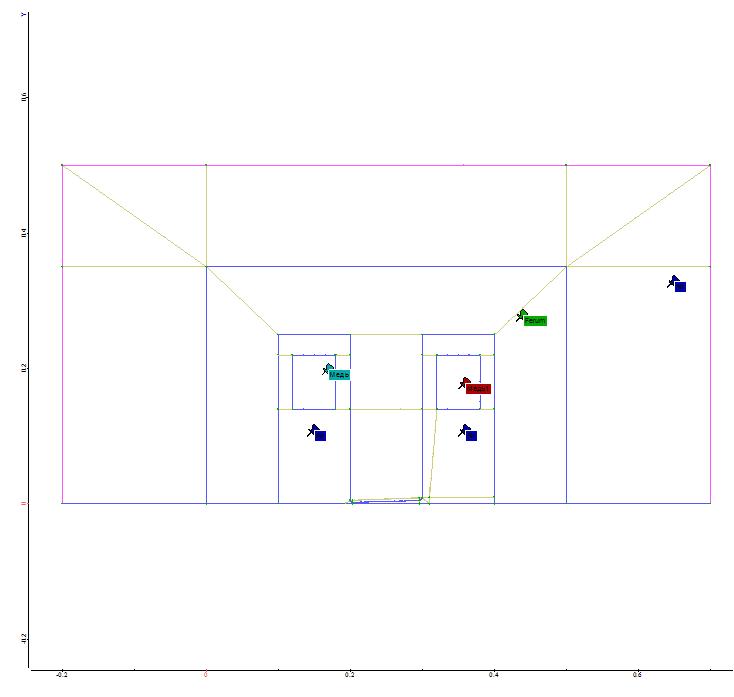
Вычисление локальных матриц и правой части, используя барицентрические координаты

Вычислим локальные матрицы и вектор правой части для реализации МКЭ с линейной аппроксимацией на треугольниках, используя барицентрические координаты. При этом будем считать, что коэффициент диффузии и источник являются на конечном элементе постоянными.

.

 

 

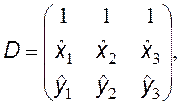
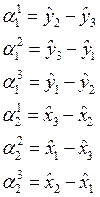
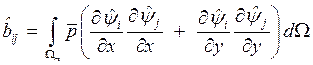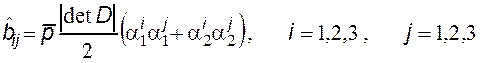
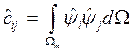
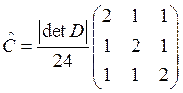
Программа сборки СЛАУ для треугольной сетки

Воспользуемся треугольной сеткой заданной в в формате препроцессора комплекса TELMA. Ниже приведена процедура сборки глобальной матрицы с заданным портретом.

c ---------------Формирование локальной матрицы--------------------Subroutine Local(ntr,xy,bc,g,nm,mas,nvtr)

Implicit double precision(a-h,o-z)

Implicit integer*4 (i-n)

common/razmer/n,n1,m

dimension xy(2,*), bc(3,3), g(3)

dimension mas(2,5),nvtr(3,*)

*    Координаты вершин треугольника

x1=   xy(1,nvtr(1,ntr))

y1=   xy(2,nvtr(1,ntr))

x2=   xy(1,nvtr(2,ntr))

y2=   xy(2,nvtr(2,ntr))

x3=   xy(1,nvtr(3,ntr))

y3=   xy(2,nvtr(3,ntr))

*   Вычисление коэффициента диффузии

p=(mas(1,nm)*4.0*3.1415926*0.0000001)

*         Площадь треугольника

d= (x2-x1)*(y3-y1) - (x3-x1)*(y2-y1)

d= dabs(d)

*         Локальный вектор правой части

do 21 i= 1,3

21     g(i)= (d/6.0)*mas(2,nm)

*         Матрица жесткости

bc(1,1)= ((y2-y3)*(y2-y3)+(x3-x2)*(x3-x2))/(2.0*d*p)

bc(2,2)= ((y3-y1)*(y3-y1)+(x1-x3)*(x1-x3))/(2.0*d*p)

bc(3,3)= ((y1-y2)*(y1-y2)+(x2-x1)*(x2-x1))/(2.0*d*p)

bc(1,2)= ((y2-y3)*(y3-y1)+(x3-x2)*(x1-x3))/(2.0*d*p)

bc(1,3)= ((y2-y3)*(y1-y2)+(x3-x2)*(x2-x1))/(2.0*d*p)

bc(2,3)= ((y3-y1)*(y1-y2)+(x1-x3)*(x2-x1))/(2.0*d*p)

do 23 i= 1,3

do 23 j= i+1,3

23                    bc(j,i)= bc(i, j)

end

c -----------------Формирование глобальной матрицы-----------------Subroutine Global(num,vector,bc,g,nvtr,ig,jg,gg,di)

Implicit double precision(a-h,o-z)

Implicit integer*4 (i-n)

common/razmer/n,n1,m

dimension vector(*),bc(3,3),g(3),nvtr(3,*)

dimension ig(*),jg(*),gg(*),di(*)

do 1 i=1,3

if (nvtr(i,num).le.n) then

di(nvtr(i,num))=di(nvtr(i,num))+bc(i,i)

vector(nvtr(i,num))=vector(nvtr(i,num))+g(i)

do 2 j=1,i-1

if (nvtr(j,num).le.n) then

i1=nvtr(i,num)

k=ig(i1)

l=k;

iflag=0

3                     continue

if (jg(l).eq.nvtr(j,num)) then

gg(l)=gg(l)+bc(i,j)

iflag=1

endif

l=l+1

if (iflag.eq.0)  goto 3

endif

2         continue

endif

1    continue

100      continue

return

end

Вывод

В результате решения программой msgnrh-m, на вход которой подавалась матрица, собранная в лабораторной работе было получено решение, которое мы сравнили с решением, полученным пакетом TELMA. Относительная погрешность (невязка), составила  2.885334e-005.