Статистические методы. Исследование отклика.

Министерство образования Российской Федерации

Кафедра прикладной математики

Лабораторная работа по статистическим методам №3

Факультет:                     ПМИ

Группа:                           ПМ-81

Студенты:                     Адаманова С.

Бобылева Д.

Фельдгендлер А.

Преподаватели:             Лисицин Д. В.         

Попов А. А.

Новосибирск – 2001

1. Постановка задачи

Значение исследуемого отклика описывается моделью y(x)=q1*f1(x)+q2*f2(x)+q3*f3(x).

2. Компьютерный листинг

I     

р=3  -  количество регрессоров.

Оценка вектора параметров :

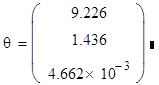RSS_p=21.218  - остаточная сумма квадратов рассчитанная по модели с р регрессорами.

С_р=3               - статистика Мэлоуса

 =0.915     - коэффициент детерминации

E_p=4.34        - среднеквадратичная ошибка предсказания 

J_p=37.132     - оценка Ротмана

II     

р=2  -  количество регрессоров.

Оценка вектора параметров :

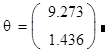RSS_p=21.236  - остаточная сумма квадратов рассчитанная по модели с р регрессорами.

С_р=1.007       - статистика Мэлоуса

 =0.914     - коэффициент детерминации

E_p=4.34        - среднеквадратичная ошибка предсказания 

J_p=30.674     - оценка Ротмана

III     

р=1  -  количество регрессоров.

Оценка вектора параметров :

RSS_p=284.182  - остаточная сумма квадратов рассчитанная по модели с р регрессорами.

С_р=98.149        - статистика Мэлоуса

 =0               - коэффициент детерминации

E_p=34.877       - среднеквадратичная ошибка предсказания 

J_p=341.018      - оценка Ротмана

Анализируя полученные результаты, приходим к выводу, что оптимальная модель имеет вид:

, подставляя оценки параметров и функции, получим:

3. Таблица

y	y	y-y	y	y	y-y
1	2.07	-1.07	9	10.71	-1.71
5	3.51	1.49	13	12.15	0.85
4	4.95	-0.95	14	13.59	0.41
7	6.39	0.61	13	15.03	-2.03
10	7.83	2.17	18	16.47	1.53
8	9.27	-1.27