Статистическая оценка надежности решений методами главных компонент и факторного анализа

1 Как видим, два последних приведенных критерия — кварти-мин и облимин — построены так, что одновременно в расчет принимаются старые значения координат элементарных признаков a_jk, значения элементов, задающих вращение латентных факторов p_kf и новые координаты признаков как результат умножения двух предыдущих значений a_jk p_kf. Оптимизируется структура каждого фактора по составу элементарных признаков (Хр j = 1,/и) и затем осуществляется обобщение на все общие факторы вращаемого пространства (W^ k, I = l,r).

Применение любого из критериев качества структуры общих факторов означает, что после каждого поворота факторного пространства проводятся расчет критерия и соответствующая оценка качества структуры факторов. Вращение завершается, когда критерий, достигнув максимального (минимального) значения, на следующем шаге алгоритма начинает отклоняться от оптимума.

Выбор угла вращения системы факторов представляется наиболее тонким вопросом при улучшении факторной структуры. Часто его решают субъективно, например, после построения графического изображения разброса точек, отображающих расположение элементарных признаков в пространстве общих факторов. Успех решения вопроса при этом во многом будет определяться опытом самого исследователя. Могут применяться и аналитические подходы, например, при ортогональном вращении тангенс наилучшего угла для поворота факторных осей рекомендуется находить по формуле [90]:

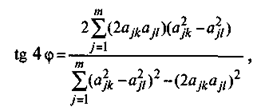
где k и / — пара факторов (F_k и F,) из матрицы факторного отображения A(k, I— \,г).

Вращение общих факторов дает возможность максимально сократить разброс субъективных суждений относительно названий (образов) общих факторов, неизменно присутствующий в факторном анализе. Тем самым методы факторного анализа из группы в большей степени теоретических методов статистики, ненадежных для аналитических выводов, как бы переходят в

ДРУГУ^Ю ГрУ^ппУ мешдив, гииклл и иизьилиющил ди^1<иичпи ди^-

товерно судить о явлениях и процессах.

7.9. Статистическая оценка надежности решений методами главных компонент и факторного анализа

Корректное решение задач при помощи методов факторного анализа предполагает подтверждение значимости исходной матрицы парных корреляций (ковариаций) и достаточности числа обобщенных факторных признаков в анализе.

Значимость корреляционной матрицы подвергается проверке, если принять во внимание, что незначимые корреляционные (ковариационные) связи элементарных признаков не дают оснований вообще для поиска обобщенных признаков. В этом случае все вычислительные собственные числа (Х^А^-Л/я) будут близки единице, и обобщенные факторы по составу становятся очень похожими на элементарные признаки. Проведение факторного анализа теряет смысл.

Проверка значимости матрицы парных корреляций осуществляется при помощи критерия Уилкса — х² > ^его наблюденное значение оценивается по формуле:

х2=-(и-£(2«+5))1п|Л|, где R — матрица парных корреляций;

п, т — соответственно число наблюдаемых объектов и число элементарных признаков в анализе.

Расчет х²-^кР^итеР^ия не представляет трудностей, так как уже на начальной стадии исследования, после получения собственных чисел Kj определитель |Л| легко находится из произт

ведения   П^у >   ^т-^е-   И =X_rX₂-...-X_m.   Наблюденное   значение

У=1

критерия Уилкса сравнивается с табличным, для %² -распределения при заданном уровне параметра а и числе степеней свободы v= 1/2 т (т - 1). Значимость корреляционной матрицы подтверждается при xh > Xa,v.