Решение
Матрица обмена А вида:
![]()
![]()
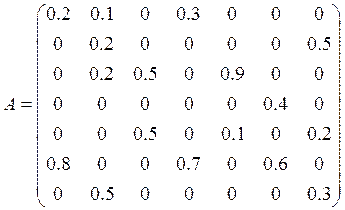
1. Реализовать алгоритм приведения матрицы обмена к каноническому виду. Для заданной матрицы обмена выделить неприводимые подмножества.
Приведение матрицы обмена к каноническому виду по алгоритму 1.
Шаг 1: В
качестве рассматриваемого множества N берем множество
всех индексов: ![]() .
.
Шаг 2:
Первый индекс из ![]()
![]() . Найдем
для него все индексы
. Найдем
для него все индексы ![]() , для которых выполняется условие
, для которых выполняется условие
![]() . Из
. Из ![]() и найденных индексов
и найденных индексов ![]() формируем подмножество
формируем подмножество ![]() :
: ![]() .
.
Шаг 3:
Берём в качестве ![]() последовательно все элементы
подмножества
последовательно все элементы
подмножества ![]() и повторяем шаг 2 до тех пор, пока оно не
перестанет пополняться. Выделенное в результате подмножество является независимым.
и повторяем шаг 2 до тех пор, пока оно не
перестанет пополняться. Выделенное в результате подмножество является независимым.
Шаг
3.2 ![]()
![]()
Новые
значения индекса ![]() включаем в подмножество
включаем в подмножество ![]() :
: ![]() .
Выделенное в результате подмножество является независимым.
.
Выделенное в результате подмножество является независимым.
Шаг 4: Для всех элементов независимого подмножества повторяем шаги 2 и 3 до тех пор, пока в нём не будут выделены все неприводимые подмножества.
![]()
![]() Шаг 4.2:
Формируем подмножество
Шаг 4.2:
Формируем подмножество ![]() :
: ![]()
Шаг
4.3: Берём в качестве ![]() последовательно все
элементы подмножества
последовательно все
элементы подмножества ![]() и повторяем шаг 2 до тех пор,
пока оно не перестанет пополняться:
и повторяем шаг 2 до тех пор,
пока оно не перестанет пополняться:
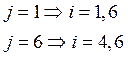
Множество ![]() .
.
![]()
![]() Шаг 4.2:
Формируем подмножество
Шаг 4.2:
Формируем подмножество ![]() :
: ![]()
Шаг
4.3: Берём в качестве ![]() последовательно все
элементы подмножества
последовательно все
элементы подмножества ![]() и повторяем шаг 2 до тех пор,
пока оно не перестанет пополняться:
и повторяем шаг 2 до тех пор,
пока оно не перестанет пополняться:
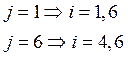
Множество ![]() .
.
![]()
![]() Шаг 4.2:
Формируем подмножество
Шаг 4.2:
Формируем подмножество ![]() :
: ![]()
Шаг
4.3: Берём в качестве ![]() последовательно все
элементы подмножества
последовательно все
элементы подмножества ![]() и повторяем шаг 2 до тех пор,
пока оно не перестанет пополняться:
и повторяем шаг 2 до тех пор,
пока оно не перестанет пополняться:
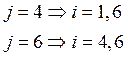
Множество ![]() .
.
Независимое
подмножество ![]() содержит независимое подмножество
содержит независимое подмножество ![]() , которое являtтся
собственным и неприводимым, поскольку не содержат других независимых
подмножеств.
, которое являtтся
собственным и неприводимым, поскольку не содержат других независимых
подмножеств.
Шаг 5:
Из рассматриваемого множества индексов ![]() вычеркиваем
те, которые вошли в выделенные неприводимые подмножества. Получаем новое
множество
вычеркиваем
те, которые вошли в выделенные неприводимые подмножества. Получаем новое
множество ![]() :
: ![]() .
.
Шаг 6: Возвращаемся на шаг 2 до тех пор, пока удаётся выделять неприводимые подмножества или пока рассматриваемое подмножество индексов не пусто.
Шаг
6.2: Находим для него все индексы ![]() , для
которых выполняется условие
, для
которых выполняется условие ![]() .
Из
.
Из ![]() и найденных индексов
и найденных индексов ![]() формируем подмножество
формируем подмножество ![]() :
: ![]() .
.
Шаг 6.3: Берём в
качестве ![]() последовательно все элементы подмножества
последовательно все элементы подмножества ![]() и повторяем шаг 2 до тех пор, пока оно не
перестанет пополняться:
и повторяем шаг 2 до тех пор, пока оно не
перестанет пополняться:
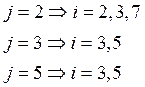
![]()
![]() -
независимое подмножество
-
независимое подмножество
Шаг 6.4: Для всех
элементов независимого подмножества ![]() повторяем шаги 2 и 3 до
тех пор, пока в нём не будут выделены все неприводимые подмножества:
повторяем шаги 2 и 3 до
тех пор, пока в нём не будут выделены все неприводимые подмножества:
Шаг 6.4.2:
![]()
Шаг 6.4.3:
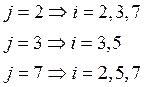
![]() - не
является неприводимым, т.к.
- не
является неприводимым, т.к. ![]()
![]()
Шаг
6.4.2: ![]()
Шаг 6.4.3:
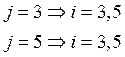
![]()
Шаг
6.4.2: ![]()
Шаг 6.4.3:
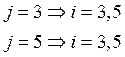
![]()
Шаг
6.4.2: ![]()
Шаг 6.4.3:
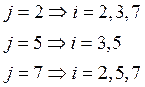
![]()
Независимое подмножество ![]() содержит независимое подмножество
содержит независимое подмножество ![]() , которое являются собственным и
неприводимым, поскольку не содержат других независимых подмножеств
, которое являются собственным и
неприводимым, поскольку не содержат других независимых подмножеств
Шаг 7: Перенумеровываем индексы
так, чтобы номера из ![]() -го неприводимого подмножества
занимали места с
-го неприводимого подмножества
занимали места с ![]() по
по ![]() , где
, где 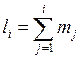 ,
, ![]() – число элементов в
– число элементов в ![]() -ом неприводимом подмножестве.
-ом неприводимом подмножестве.
Соответствие старых индексов в искомой матрице обмена А и в приведенной к канонической форме:
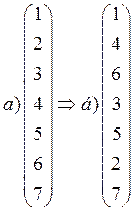
Матрица обмена в канонической форме:
|
0,2 |
0,3 |
0 |
0 |
0 |
0,1 |
0 |
|
0 |
0 |
0,4 |
0 |
0 |
0 |
0 |
|
0,8 |
0,7 |
0,6 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0,5 |
0,9 |
0,2 |
0 |
|
0 |
0 |
0 |
0,5 |
0,1 |
0 |
0,2 |
|
0 |
0 |
0 |
0 |
0 |
0,2 |
0,5 |
|
0 |
0 |
0 |
0 |
0 |
0,5 |
0,3 |
Приведение матрицы обмена к каноническому виду по алгоритму 2:
Матрица обмена А вида:
![]()
![]()
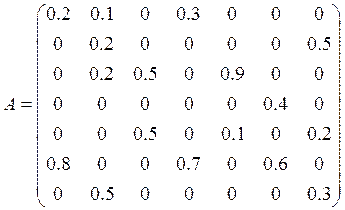
Шаг 1: Рассматриваем множество индексов ![]() .
.
Из множества ![]() выделяем в отдельные
неприводимые подмножества такие индексы
выделяем в отдельные
неприводимые подмножества такие индексы ![]() , для
которых выполняется равенство
, для
которых выполняется равенство ![]() ,
но подобных элементов
,
но подобных элементов ![]() не
имеется в матрице обмена, т.е. и соответствующих неприводимых подмножеств нет.
не
имеется в матрице обмена, т.е. и соответствующих неприводимых подмножеств нет.
Шаг2: Для каждого
индекса ![]() формируем подмножество
формируем подмножество
![]()
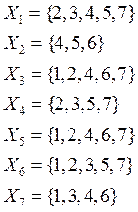
Шаг 3: Выделяем
класс индексов ![]() максимально большей размерности,
входящий в два и более подмножества
максимально большей размерности,
входящий в два и более подмножества ![]() :
:![]() .
.
Шаг 4: Пусть ![]() размерность
размерность ![]() ,
, ![]() – количество подмножеств
– количество подмножеств ![]() , в которые входит
, в которые входит ![]() ,
,
![]() – общее количество стран, участвующих в
обмене, тогда, если выполняется равенство
– общее количество стран, участвующих в
обмене, тогда, если выполняется равенство ![]() ,
выделяем неприводимое подмножество, включая в него все
,
выделяем неприводимое подмножество, включая в него все ![]() ,
для которых
,
для которых ![]() :
: ![]() - первое
неприводимое множество.
- первое
неприводимое множество.
Шаг 5: Повторяем шаги 3 и 4 до тех пор, пока удаётся выделить класс
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.