







3. Методические указания к выполнению задания.
1. Типовой расчет выполняется на бумаге формата А4, записи ведутся на лицевой стороне, титульный лист оформляется по установленному в университете образцу.
2. Все интегралы в типовом расчете считать с использованием основной теоремы о вычетах, не прибегая к помощи таблиц и справочников.
3.
Вычисления проводить для двух
случаев, ![]() и
и ![]() (
(![]() -параметр передаточной функции,
-параметр передаточной функции, ![]() - параметр входного сигнала).
- параметр входного сигнала).
4. Вычисления проводить дважды: методами частотных и импульсных характеристик.
5.
Там, где необходимо, использовать
представление ![]() - функции интегралом Фурье
- функции интегралом Фурье ![]() и определяющими эту функцию свойствами
и определяющими эту функцию свойствами 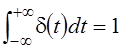 ,
, ![]() .
.
4. Теоретические сведения
Рассмотрим линейную систему, описываемую дифференциальным уравнением с постоянными коэффициентами
![]() , (1)
, (1)
где ![]() ,
, ![]() - оператор дифференцирования,
- оператор дифференцирования, ![]() - входной сигнал (реализация стационарного
случайного процесса),
- входной сигнал (реализация стационарного
случайного процесса), ![]() - сигнал на выходе системы. В
изображениях по Лапласу уравнение (1) имеет вид
- сигнал на выходе системы. В
изображениях по Лапласу уравнение (1) имеет вид
![]() , (2)
, (2)
где ![]() - передаточная функция
фильтра,
- передаточная функция
фильтра, ![]() ,
, ![]() . Если
. Если ![]() , то
, то ![]() -
импульсная функция фильтра, при этом, в силу
-
импульсная функция фильтра, при этом, в силу ![]() , имеем
, имеем ![]() , т.е.
, т.е.
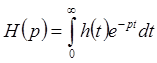 (3)
(3)
Если система устойчива (![]() абсолютно интегрируема, все полюсы
абсолютно интегрируема, все полюсы ![]() лежат в левой полуплоскости комплексной
плоскости
лежат в левой полуплоскости комплексной
плоскости ![]() ), то
), то ![]() и
и ![]() связаны преобразованием Фурье,
связаны преобразованием Фурье,
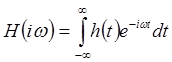 , (4)
, (4)
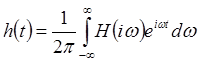 . (5)
. (5)
Для физически реализуемых систем ![]() при
при ![]() .
.
Пусть ![]() -
стационарный процесс с нулевым средним
-
стационарный процесс с нулевым средним ![]() , ковариационной
функцией
, ковариационной
функцией ![]() и спектральным представлением
и спектральным представлением
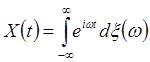 (6)
(6)
Функция интенсивности ![]() процесса
процесса
![]() называется спектральной плотностью
процесса
называется спектральной плотностью
процесса ![]() и связана с
и связана с ![]() преобразованием
Фурье (формулами Винера-Хинчина):
преобразованием
Фурье (формулами Винера-Хинчина):
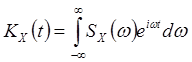 (7)
(7)
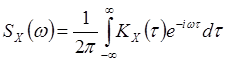 (8)
(8)
Согласно
(2), (6) процесс ![]() на выходе системы записывается в
виде стохастического интеграла
на выходе системы записывается в
виде стохастического интеграла ![]() . Поэтому
. Поэтому
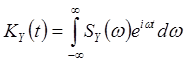 , (10)
, (10)
![]() , (11)
, (11)
Взаимная ковариационная функция стационарно связанных процессов ![]() и
и ![]() определяется
выражением [2, стр.252]
определяется
выражением [2, стр.252]
![]()
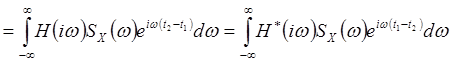 . (12)
. (12)
Чтобы записать выражения для ![]() и
и
![]() в терминах импульсной функции
в терминах импульсной функции ![]() , вместо (6) и (9) используют представления
, вместо (6) и (9) используют представления
![]() и
и ![]() в виде среднеквадратических
интегралов
в виде среднеквадратических
интегралов
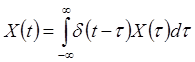 , (13)
, (13)
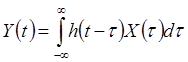 (14)
(14)
Из (13), (14) следует, что
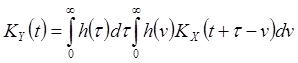 , (15)
, (15)
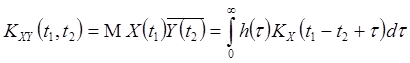 . (16)
. (16)
Положив ![]() , можем записать (12) и
(16) в виде
, можем записать (12) и
(16) в виде
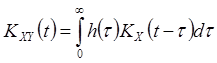 (17)
(17)
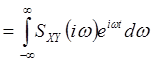 , (18)
, (18)
где
![]() (19)
(19)
Отметим, что, в общем случае, взаимная ковариационная функция не является четной.
Из (9), (14) получаем выражения для
среднего процесса ![]() ,
,
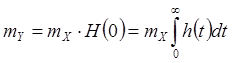 (20)
(20)
а из (10), (15) - для его дисперсии,
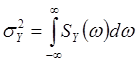 (21)
(21)
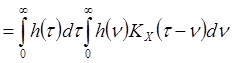 (22)
(22)
Интервал корреляции ![]() случайного процесса
случайного процесса ![]() вычисляется по формуле
вычисляется по формуле
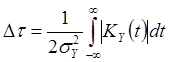 . (23)
. (23)
Ковариационную функцию производной ![]() находим, дважды
дифференцируя
находим, дважды
дифференцируя ![]() ,
,
![]() , (24)
, (24)
а дисперсию ![]() - по формулам
- по формулам
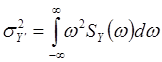 (25)
(25)
![]() . (26)
. (26)
5. Решение типового варианта.
Случайное напряжение ![]() подается
на вход системы
подается
на вход системы
|
|
с выхода которой снимается случайное напряжение ![]() .
.
Вычисление ![]() и
и ![]()
Согласно (2), (4) при ![]() имеем
имеем
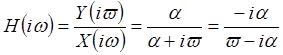 ,
, 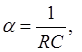
Положим ![]() ,
, ![]() . Используя основную теорему о вычетах [5], согласно
(5) находим
. Используя основную теорему о вычетах [5], согласно
(5) находим
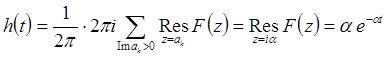 (24)
(24)
Указание. При нахождении вычета функции вида ![]() с полюсом
с полюсом ![]() кратности
кратности
![]() использовать формулу
использовать формулу ![]() . В частности, в (24)
. В частности, в (24) ![]() ,
, ![]() ,
, ![]() .
.
Вычисление ![]()
Согласно (8) находим
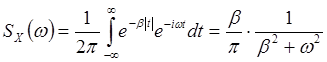
Отдельно рассмотрим варианты ![]() и
и
![]() .
.
Случай ![]() . Метод частотных характеристик. Согласно (11)
имеем
. Метод частотных характеристик. Согласно (11)
имеем
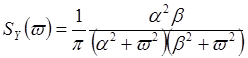 .
.
Функция ![]() имеет в верхней
полуплоскости два простых полюса,
имеет в верхней
полуплоскости два простых полюса, ![]() и
и ![]() . Следовательно, согласно (10) при
. Следовательно, согласно (10) при ![]() получаем
получаем
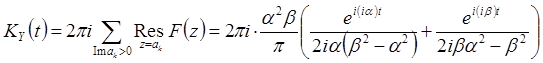
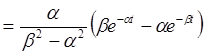 ,
, ![]() .
.
Интегрируя аналогичным образом при ![]() и объединяя полученный результат с
предыдущим, получаем окончательный результат
и объединяя полученный результат с
предыдущим, получаем окончательный результат
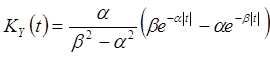 ,
, ![]() ,
,
Указание. При ![]() использовать формулу
использовать формулу ![]() , а при
, а при ![]() - формулу
- формулу
![]() .
.
Наконец, согласно (21) находим дисперсию сигнала на выходе системы,
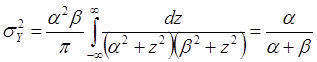 .
.
Метод импульсных характеристик. Согласно (15) при ![]() имеем
имеем
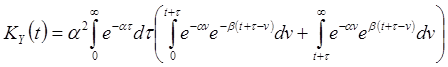
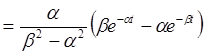 .
.
С учетом четности ![]() результат
вычислений совпадает с полученным выше. Далее по формуле (22) получаем
результат
вычислений совпадает с полученным выше. Далее по формуле (22) получаем
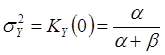 , что опять совпадает с предыдущим результатом.
, что опять совпадает с предыдущим результатом.
График функции ![]() представлен
на рис. 1. В точке
представлен
на рис. 1. В точке ![]() функция имеет гладкий максимум.
функция имеет гладкий максимум.
|
|
Рис. 1. Ковариационная функция ![]() ,
,
![]() .
.
Случай ![]() . Метод частотных
характеристик. Функция
. Метод частотных
характеристик. Функция
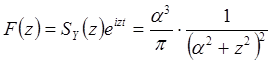
имеет в верхней полуплоскости полюс ![]() кратности
кратности ![]() . Следовательно,
при
. Следовательно,
при ![]() получаем
получаем
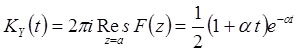 .
.
Объединяя этот результат с результатом интегрирования
при ![]() , заключаем, что
, заключаем, что
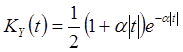 .
.
Указание. При нахождении вычета функции ![]() относительно
полюса
относительно
полюса ![]() кратности
кратности ![]() использовать
формулу [5,6,8]
использовать
формулу [5,6,8]
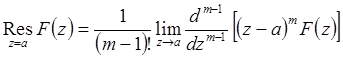
Метод импульсных характеристик. Используя соотношение (15), при ![]() получаем
получаем
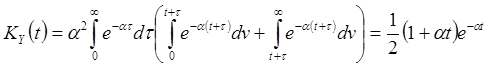 ,
,
|
|
Рис. 2. Функция ![]()
что приводит к тому же результату, что и выше. График
функции ![]() при
при ![]() представлен
на рис.2. В точке
представлен
на рис.2. В точке ![]() она имеет гладкий максимум,
равный
она имеет гладкий максимум,
равный
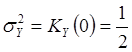 .
.
Вычисление ![]() .
.
Случай ![]() . Метод частотных
характеристик. Функция
. Метод частотных
характеристик. Функция
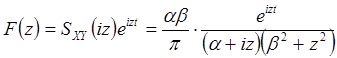
имеет в верхней полуплоскости два полюса, ![]() и
и ![]() , а в
нижней полуплоскости – один полюс
, а в
нижней полуплоскости – один полюс ![]() . Следовательно, при
. Следовательно, при ![]() получаем
получаем
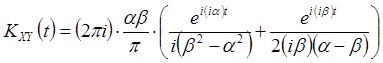
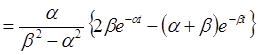 .
.
Если ![]() , то
, то
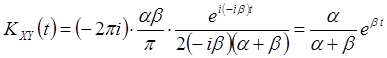 .
.
Метод импульсных характеристик. Вычисления согласно (17) при ![]() дают
следующий результат:
дают
следующий результат:
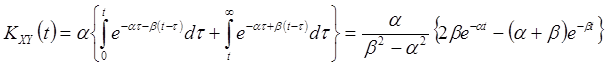 .
.
При ![]() по той же формуле (17)
получаем
по той же формуле (17)
получаем
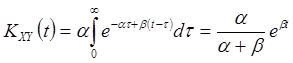 .
.
Случай ![]() . Метод частотных
характеристик. Функция
. Метод частотных
характеристик. Функция
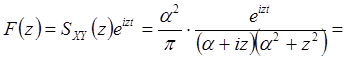
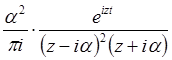
имеет в верхней полуплоскости полюс ![]() кратности 2, а в нижней – простой полюс
кратности 2, а в нижней – простой полюс ![]() . Следовательно, при
. Следовательно, при ![]() получаем
получаем
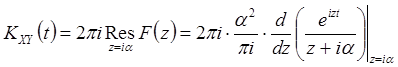
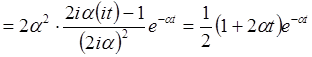 .
.
Если ![]() , то
, то
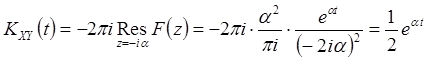 .
.
Метод импульсных характеристик. Действуем так же, как в случае ![]() (см. выше), но непосредственно перед
интегрированием учитываем, что
(см. выше), но непосредственно перед
интегрированием учитываем, что ![]() .
.
Вычисление ![]()
Случай ![]() . Поскольку
. Поскольку ![]() для всех
для всех ![]() , то
согласно (23) получаем
, то
согласно (23) получаем
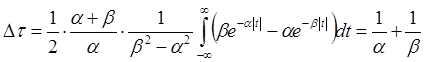
Случай ![]() . В данном случае
. В данном случае ![]() и
и ![]() . Поэтому
аналогично предыдущему находим
. Поэтому
аналогично предыдущему находим
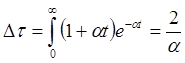
Отсюда видим, что оба выражения для ![]() при
при ![]() и
и ![]() можно объединить в одно, а именно
можно объединить в одно, а именно
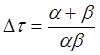 .
.
Вычисление ![]()
Процесс ![]() непрерывен
(в среднеквадратическом), так как функция
непрерывен
(в среднеквадратическом), так как функция
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.