Решение системы линейных алгебраических уравнений методом простой итерации

Задание

Решить систему линейных алгебраических уравнений методом простой итерации.

Ход работы

Решение системы осуществляется по итерационной схеме, используя формулу:

где – вектор решения на текущей итерации,

– вектор решения на предыдущей итерации,

b – вектор правой части, 

– весовой коэффициент.

Этот метод обеспечивает сходимость метода при условии, что весовой коэффициент положительный и меньше единицы.

Реализация алгоритма простой итерации.

Исходная матрица разрезается на блоки. Т.к. размерность матрицы может нацело не делиться на число компьютеров в топологии, блоков существует два типа,:

1.  блок ширины L, где L определяется следующим образом: 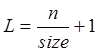, где n – размерность матрицы системы, size – число компьютеров в топологии.

2.  блок ширины L–1.

Таким образом, получаемая реализация разреза такова: сперва выделяются блоки шириной L, а затем блоки шириной L–1.

Таким же образом происходит разрезание векторов правой части и решения на текущей и предыдущей итерациях.

Main ()

{

{Size-1 компьютер производит считывание и рассылку данных всем остальным}

Continue: // метка продолжения счета

{Увеличить количество итераций}

{Умножить матрицу на вектор ()}

{Вычислить решение на текущей итерации: }

if (Условие выхода выполняется)

{Вывести результаты}

else

{Продолжить вычисления (goto continue)}

}

Компьютер, имеющий номер size–1, считывает матрицу и вектор правой части и рассылает всем остальным. После получения данных, происходит умножение матрицы на вектор, используя алгоритм пересылки данных по кольцу, и далее, вычисление решения на текущей итерации.

После получения решения каждый компьютер проверяет по своей части вектора решения условие выхода и посылает полученную информацию компьютеру с номером 0. Нулевой компьютер проводит анализ полученной информации и рассылает всем остальным решение об окончании или продолжении счета.

После окончания счета все компьютеры отсылают свои части вектора решения нулевому компьютеру.

Результаты

Проведем следующие исследования:

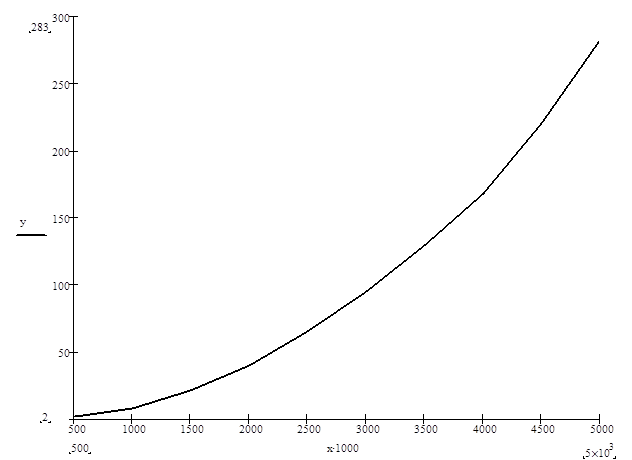
1.  время счета в зависимости от размерности задачи;

2.  при некоторой фиксированной размерности (n=N) построить график зависимости времени счета от числа процессоров в осях t, np.

Для исследований выберем матрицу следующего вида:

А =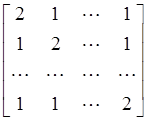

Эта матрица является невырожденной, следовательно, система линейных алгебраических уравнений с такой матрицей имеет единственное решение.

Для простой проверки правильности решения будем формировать правую часть таким образом, чтобы вектор решений был единичным.

Время счета в зависимости от размерности задачи

Размерность	Время счета, сек
500	2
1000	8
1500	21
2000	40
2500	65
3000	95
3500	129
4000	168
4500	220
5000	283

Зависимость времени счета от числа процессоров при размерности системы N=3000

Число процессоров	Время, сек
1	95
2	95
3	97
4	95
5	95
6	95
7	95
8	95

Вывод:

1.  По результатам 1^го теста мы получили, что при увеличении размерности системы увеличивается и время счета.

2.  Исходя из результатов 2^го теста, мы получили, что для метода простой итерации практически нет разницы на скольких процессорах считать (на тесте где размерность системы N=3000, на любом количестве процессоров от 1 до 8 было получено практически одно и тоже время, порядка 95 сек.), поэтому можно поставить под сомнение необходимость распараллеливания данного метода.

Программа

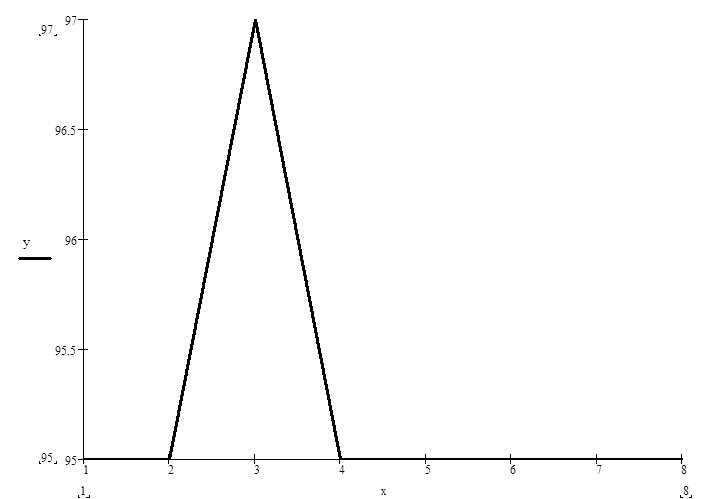#include "mpi.h"

#include <stdio.h>

#include <time.h>

#include <math.h>

#define ND 1

#define Eps 1.e-08

double **A, *Y1, *Y0, *Result, tau;

int n,m,L,iter=0;

time_t starttime,finishtime;

int main( int argc, char *argv[])

{

int tag=11,rank,size,start;

MPI_Status st; MPI_Comm ring;

int dims[ND],per[ND],reord=0,prev,next;

int i,j,k,dim,d;

FILE *fp;

int flag=0;

int recv_flag=0;

MPI_Init(&argc,&argv);

MPI_Comm_rank(MPI_COMM_WORLD,&rank); //computer number

MPI_Comm_size(MPI_COMM_WORLD,&size); //total number of computers

per[0]=1; //ring