Решение систем линейных алгебраических уравнений методом Гаусса с помощью различных алгоритмов

Задание

Решение систем линейных алгебраических уравнений методом Гаусса.

Постановка задачи

Необходимо найти решение системы линейных алгебраических уравнений вида

Ах = b

где А – матрица размера n x n, x – вектор неизвестных, b – вектор правых частей.

Первый алгоритм.

Исходная матрица А делится на блоки шириной m, где m = , size –  число компьютеров, и блоки рассылаются по компьютерам, соответственно 1 блок – компьютеру с номером 0, 2 блок – компьютеру с номером 1 и т.д.

После деления матрицу необходимо привести к диагональному виду, используя элементарные преобразования, а именно: умножение строки на ненулевое число, перестановка строк и добавления одной строки к другой, умноженной на ненулевое число. Соответствующие преобразования производятся с вектором правых частей. Приведение матрицы к диагональному виду начинает 0-й компьютер с посылки своей нулевой строки всем остальным и начинает обнулять свой блок. Другие компьютеры принимают эту строку и производят обнуление своего блока. После окончания 0-й компьютер посылает остальным свою первую строку и т.д. После окончания процесса будем иметь матрицу, где ненулевыми элементами являются элементы верхнего треугольника.

Начиная с последней строки матрицы, выполняем обратный ход и находим вектор решений системы.

Второй алгоритм.

Исходная матрица А также делится на блоки шириной m, где m = , size –  число компьютеров. После этого у каждого компьютера формируется свой блок следующим образом: строка с номером 0 отправляется 0-му компьютеру, строка с номером 1 – 1-му и т.д., строка с номером size-1 компьютеру, имеющему номер size-1. Строка с номером size –  0-му компьютеру, строка size+1 – 1-му и т.д. После формирования блоков для каждого компьютера выполняется приведение матрицы к треугольному виду, используя элементарные преобразования.

Нулевой компьютер отсылает свою 0-ю строку всем остальным компьютерам и начинает преобразовывать свой блок. Остальные, приняв 0-ю строку от 0-го компьютера, выполняют преобразования над своими блоками. После окончания преобразований 1-й компьютер отсылает свою 0-ю строку всем остальным, и  сам начинает преобразовывать свой блок. Все остальные, кроме 0-го, приняв строку, начинают преобразовывать свои блоки (полностью), а 0-й преобразовывает не весь свой блок, а только часть, исключив свою 0-ю строку. И т.д. В результате будем иметь матрицу с ненулевыми элементами в верхнем треугольнике.

Начиная с последней строки, выполняем обратный ход и находим решение системы линейных алгебраических уравнений.

Результаты.

Произведём сравнение двух алгоритмов. Для сравнения будем пользоваться матрицей следующей структуры:

А =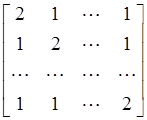

Эта матрица является невырожденной, следовательно, система линейных алгебраических уравнений с такой матрицей имеет единственное решение.

Для простой проверки правильности решения будем формировать правую часть таким образом, чтобы вектор решений был единичным.

Размерность системы	t сек, первый алгоритм	t сек, второй алгоритм
100	0	0
240	1	1
500	6	4
752	16	13
1000	36	28

Вывод: исходя из полученных результатов, можно сделать вывод, что второй алгоритм Гаусса является более быстрым, чем первый на матрицах большой размерности. Разница заметна уже на матрицах размерности 500 х 500.

Программа

Первый алгоритм

#include <mpi.h>

#include <stdio.h>

#include <time.h>

#define ND 1

#define eps 1.e-08

//#define N 4  //Number of rows in

//#define M 16 //Number of columns in

void kill_all (MPI_Comm ring)

{

FILE *fp;

fp=fopen("output.txt","wt");

fprintf(fp,"Решение не найдено.\n");

fclose(fp);

MPI_Abort(ring,1);

}

double **A, *V;

int n,m;

time_t starttime,finishtime;

main (int argc, char** argv)

{

int tag=11,rank,size;

MPI_Status st; MPI_Comm ring;

int dims[ND],per[ND],reord=0,prev,next;

double d,s;

int i,j,k,l;

FILE *fp;

int flag=0;

int recv_flag=0;

MPI_Init(&argc,&argv);

MPI_Comm_rank(MPI_COMM_WORLD,&rank); //computer number

MPI_Comm_size(MPI_COMM_WORLD,&size); //total number of computers

per[0]=1; //ring

dims[0]=0; //for auto creation

MPI_Dims_create(size,ND,dims);

MPI_Cart_create(MPI_COMM_WORLD,ND,dims,per,reord,&ring); //создание топологии

//Read data from file (last comp. do it)

if (rank == (size-1))

{ //Read matrix dimension and sent it to others

fp=fopen("input.txt","rt");

fscanf(fp,"%d",&n);

for (i=0;i<size-1;i++)

MPI_Send(&n,1,MPI_INT,i,tag,ring);

m=n/size; //Calculate the width

//Выделение памяти под массив (A U b)

A=(double**)malloc(m*sizeof(double*));

for (i=0;i<m;i++)

A[i]=(double*)malloc((n+1)*sizeof(double));

//Считывание матрицы А и вектора В из файла

for(i=0;i<size;i++)

{ for (j=0;j<m;j++)

for(k=0;k<n+1;k++)

fscanf(fp,"%lf",&A[j][k]);

if (i!=size-1) 

{

for(j=0;j<m;j++)

MPI_Send(A[j],(n+1),MPI_DOUBLE,i,tag,ring);

}

}       

fclose(fp);

}

else

{

//Получить размерность от последнего

MPI_Recv(&n,1,MPI_INT,size-1,tag,ring,&st);

//Выделить память под А и В

m=n/size;

A=(double**)malloc(m*sizeof(double));

for (i=0;i<m;i++)

A[i]=(double*)malloc((n+1)*sizeof(double));