в общем величины самих регрессионных коэффициентов с уменьшением числа предикторов колеблются незначительно. Но критерии надежности модели и ее параметров отличаются существенно и для а = 0,05 четыре уравнения, кроме первого, по /'-критерию нельзя считать адекватными реальным данным, с некоторой натяжкой исключение допустимо сделать для j>3. Так же резко снижаются и значения /-критериев надежности регрессионных коэффициентов. Следует обратить внимание, что выводы о малой значимости главной компоненты F4 по Х4 = 0,344 подтверждаются и ее низкой /-оценкой в регрессионной модели. Для компоненты F5 с Х5 = 0,09 регрессионный критерий / = 11,6 указывает на ее существенность в уравнении, при решении вопроса об исключении F5 следовало бы провести более глубокую логическую и критериальную проверку. В целом же на примере первой регрессионной модели (у{)видно, что с помощью обобщенных факторных признаков (главных компонент) реально построить хорошую линейную регрессию с высокой адекватностью и значительной объясняющей способностью (Л2 = 0,999).
Продемонстрированные примеры практического приложения метода главных компонент в кластерном и корреляционно-регрессионном анализе представляют в общем возможности и методов факторного анализа.
7.5. Разложение дисперсии в факторном анализе
Методы факторного анализа базируются на реальной оценке самой возможности исследования явлений. Здесь заранее при-, нимается, что общими факторами объяснить вариацию элемен тарных признаков на 100% нельзя, некоторая часть вариации ос тается скрытой характерностью изучаемого явления. Стандарта-^ зованное значение признака по /-му наблюдаемому объекту при этом представляется линейной зависимостью вида: <
![]()
где djj — латентный признак, обобщающий нераскрываемую, характерную вариацию элементарного признака;
а/ — весовой коэффициент при характерном факторе.
Уравнение функциональной зависимости Zy от Fr и D перепишем, введя обобщающий знак суммирования:
![]()
|
|
Как известно, дисперсия стандартизованной величины равна единице: D (zy) = 1, но одновременно Возведем в квадрат правую часть дисперсионного равенства:
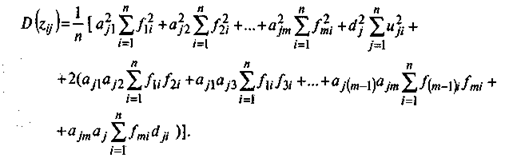
|
где г — коэффициент корреляции. Таким образом, можем записать: |
|
|
Здесь запись произведений упрощается с учетом аксиом ор-тонормированного пространства, в котором:
|
|
При условии линейной независимости общих факторов: rfkfi =0' в послеДнем равенстве выражение в скобках обращается в ноль, в итоге дисперсия стандартизованной величины раскладывается по оценкам дисперсии общих факторов и характерности:
![]()
Метод главных компонент может рассматриваться как частный от приведенного выше случай, когда
![]()
т
Назовем J^ajr общностью, это доля общей дисперсии, котог=\
рая поддается объяснению через общие факторы. Обозначим ее
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.