Основные стратегии решения задач. Задача о Ханойских башнях.

Министерство Образования

Российской Федерации

НГТУ

кафедра ПС и БД

Лабораторная работа № 2

по курсу: «Системы искусственного интеллекта»

Факультет ПМИ

Студенты:   Казыгашев К.С.    (ПМ – 15)

Корсун М.М.        (ПМ – 15)

Куликов И.М.      (ПМ – 15)

Царапкин В.А.     (ПМ – 13)

Преподаватели:    Пономаренко В.

Ванюкевич О.

Новосибирск

2005

1. Задание

Изучение   основных   стратегий    решения   задач. Приобретение  навыков  выбора  адекватных  стратегий  для решения конкретных  проблем,  возникающих на  практике. Выбор адекватного инструмента для реализации этих стратегий. Рассмотреть задачу о «Ханойских башнях».

2.  Анализ задачи

Задача о «Ханойских башнях» возникла в древней Индии, и её классическая постановка была следующей: на одном из трёх столбов были надеты 64 камня, различные по массе. Требовалось перенести камни на другой столбец, перемещая в единицу времени только один камень, используя два других столба и при этом больший камень нельзя было ставить на мене тяжёлый. Согласно легенде наступление апокалипсиса должно совпасть с перемещением последнего камня, то есть с решением задачи, причём один камень перекладывался с одного столба на другой за один день. Далее мы оценим количество дней, требуемых для перемещения камней.

Идея решения данной задачи состоит в сведении общей задачи к задачам меньшей размерности, то есть при перемещении  камней задача сводится к перемещению верхних  камней, затем перемещением на нужное место нижнего камня и только потом перемещение  камней на больший камень. Фактически данное решение можно представить в виде И/ИЛИ-графа. Который схематически представляется в виде:

   

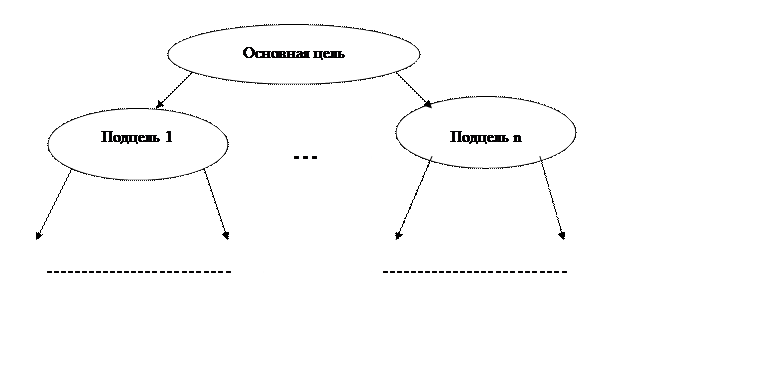
Здесь мы пока не уточняем цели для данной задачи, так как ещё не определили формально сами эти цели. Составим формальную модель. Определим задачи:

Можно Переместить Камни (Количество, Схема, Исходный столб, Вспомогательный столб, Результирующий столб).

Можно Переместить Камень (Исходный столб, Результирующий столб).

Первый задача осуществима, когда данное количество камней можно перенести по данной схеме с исходного столба на результирующий столб, с помощью вспомогательного столба. Вторая задача осуществима, когда можно переместить камень с одного столба на другой. Естественно переменная схема есть последовательность действий, связанной с перемещением данного количества камней с одного столба на другой, включает в себя правила перемещения камней. Тогда определив формально схему, как допустимую последовательность действий перемещения камней, и определив данные задачи как предикаты первого порядка, то решение задачи можно представить как истинность следующего высказывания:

То есть сначала с исходного столба на вспомогательный с помощью результирующего столба перемещается горка без одного (нижнего) элемента. Затем перемещается нижний элемент на результирующий столб. И потом горка перемещается на результирующий столбец.

Теперь можно изобразить И/ИЛИ-граф для данной задачи.

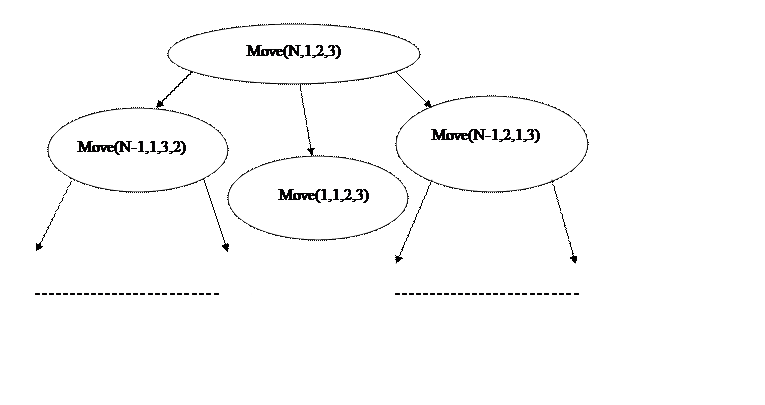
Формулируя задачу в рекуррентной форме, получим следующую схему:

move(count,n1,n2,n3) :

                    if count = 1 then

                              n1 to n3

                    endif

                    move(count-1,n1,n3,n2)

                    move(1,n1,n2,n3)

                    move(count-1,n2,n1,n3)

Приведём пример графа переходов для данной схемы, при условии, что количество камней равно 3 (стрелками обозначен обход графа):  

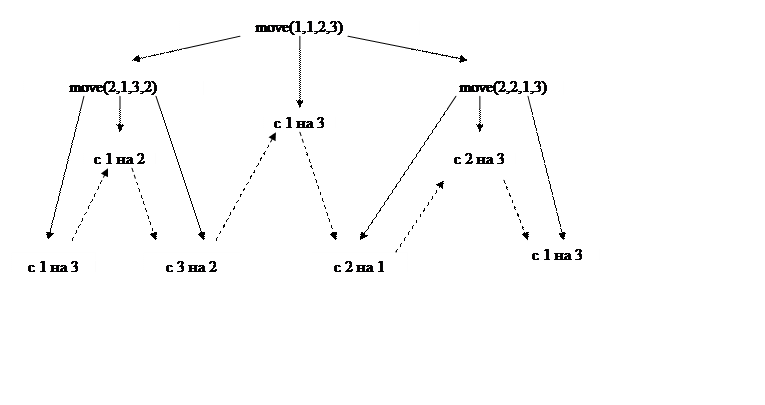
Исходя из данного графа, можно сказать, что обход осуществляется в глубину, так как вначале осуществляется спуск до листа дерева, затем подъём до корня и затем спуск по другому поддереву.

В заключении представим работу программы для перемещения трёх камней, результат которой можно сравнить с приведённым выше деревом:         

***** Start ******

Collumn 1/ -3--2--1- /

Collumn 2 / - /

Collumn 3 / - /

************

Collumn 1/ --3--2- /

Collumn 3 / --1-/

Collumn 2 / - /

************

Collumn 3/ --1- /

Collumn 1 / --3-/

Collumn 2 / --2- /

************

Collumn 1/ --3- /

Collumn 2 / --2--1-/

Collumn 3 / - /

************

Collumn 2/ --2--1- /

Collumn 3 / --3-/

Collumn 1 / - /

************

Collumn 2/ --2- /

Collumn 1 / --1-/

Collumn 3 / --3- /

************

Collumn 1/ --1- /

Collumn 2 / -/

Collumn 3 / --3--2- /

************

--3--2--1Текст программы:

/*

Hanoy town

Authors: Kazygashev,

Korsun,

Kulikov,

Tsarapkin

*/

domains

list = integer*

predicates

put(integer,                                    /* count */

integer,integer,integer,            /* number */

list,list,list,                                 /* old list */        

list,list,list,                                 /* new list */      

integer,integer,integer)            /* number collumn */      

outlist(list)

goal

write("***** Start ******"),nl,

put(3,1,2,3,[1,2,3],[],[],LR1,LR2,LR3,1,2,3),

outlist(LR1),nl,

outlist(LR2),nl,

outlist(LR3).

clauses

outlist([]) :write("-").

outlist([El|L]) :-

outlist(L),

write("-",El,"-").               

put(1,N1,N2,N3,

[El|L1], L2, L3,

L1, L2, [El|L3],

NUM1, NUM2, NUM3 ) :write("Collumn ",NUM1,"/ "),

outlist([El|L1]),write(" / "),

write("Collumn ",NUM2," / "),

outlist(L2), write("/ "),

write("Collumn ",NUM3," / "),

outlist(L3), write(" /"),nl,

write("************"),nl,

readchar(_).

put(N,N1,N2,N3,L1,L2,L3,NL1,NL2,NL3,NUM1,NUM2,NUM3) :NUM = N-1,

put(NUM, N1, N3, N2, L1, L3, L2,                             /* Old list */

NTL1_1, NTL1_3, NTL1_2,     /* New temp list 1 */

NUM1, NUM3, NUM2),

put(1, N1, N2, N3,  NTL1_1,NTL1_2,NTL1_3,      

NTL2_1,NTL2_2,NTL2_3,        /* New temp list 2 */

NUM1, NUM2, NUM3),

put(NUM, N2, N1, N3, NTL2_2,NTL2_1,NTL2_3,

NL2,NL1,NL3,                            /* Result new list */

NUM2,NUM1,NUM3).