Моделирование смешаного генератора псевдослучайных величин. Алгоритм моделирования

МО РФ

НГТУ

Кафедра прикладной математики

Лабораторная работа 1

По предмету “Моделирование в экономике”

Факультет:  ПМИ

Группа:        ПМ-92

Студентка:   Занданова Ю.Л.

Преподаватель: Самочернов  И.В.

Новосибирск 2003

1.Задание

а) Смоделировать  смешанный генератор псевдослучайных величин

б) Найти методом обратной функции моделирующее выражение для случайной величины , имеющей заданную плотность распределения:

в)  Написать алгоритмы моделирования случайной величины  с плотностью f(x) по методу исключений

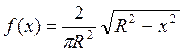
2.Выполнение

а) Для выполнения задания необходимо выбрать константы, входящие в выражение.

Выберем  , а n=250 (число генерируемых значений  в выборке). При таких значениях  период равен 250.

Используя программный  пакет ISW4.0, сравним эмпирическое и равномерное распределения, проверяя при этом вероятность совпадения по различным критериям. Результаты :

Хи-квадрат Пирсона c попр.Никулина S=2.6633e-27 P=1      

Колмогорова S=0.058259 P=1      

Смирнова S=0.013576 P=1      

Омега-малое кв. Мизеса S=0.00058331 P=1      

Омега-большое кв. Мизеса S=0.0094074 P=1      

Для иллюстрации приведем следующие графики:

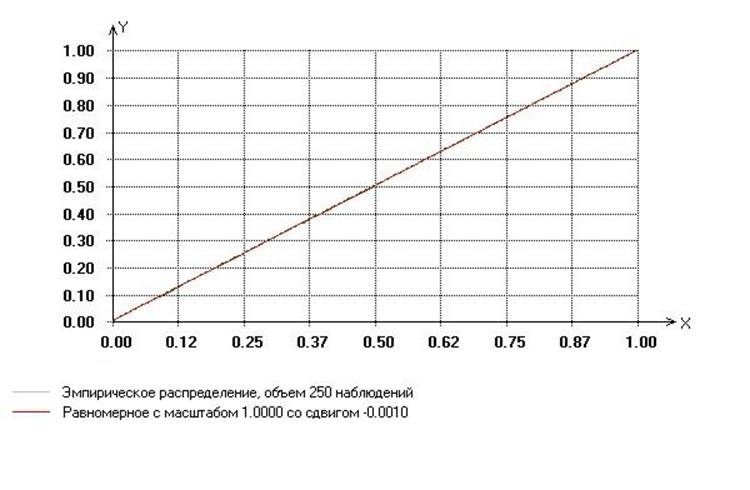
График плотности распределения равномерной и эмпирической функций :

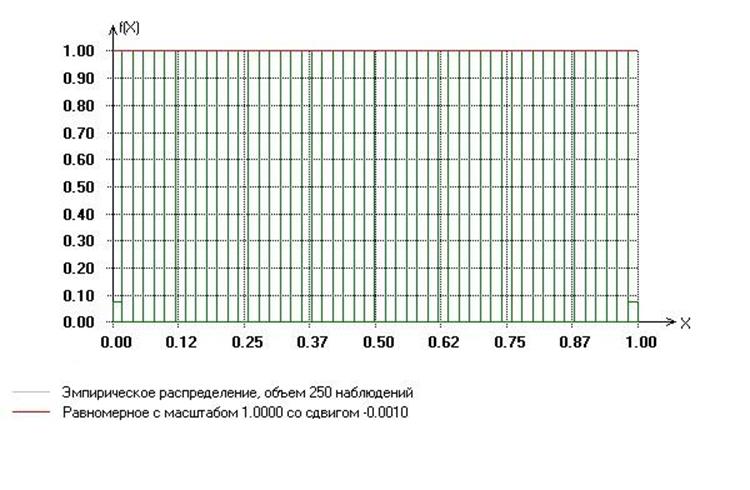
После сравнения становиться очевидно, что  генерируемые числа  практически соответствуют случайным числам, подчиненным равномерному закону распределения.

б) метод обратных функций

Будем моделировать случайную величину  =случайная величина, подчиненная нормальном закону распределения.

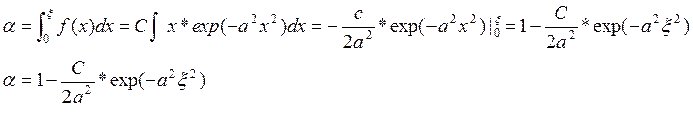
Выполнив соответствующие преобразования для реализации метода, получим формулу для генерации случайных величин

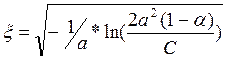,где a=0.1,

Константу С получим из условия  

C=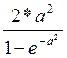

При  а=3   С=18.002;  случайное число.

График функции  распределения F(x)=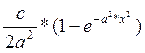

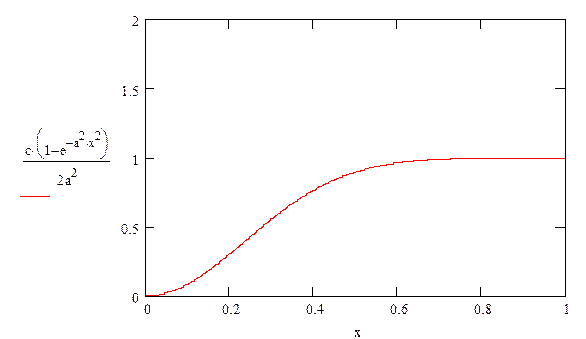
График функции плотности распределения

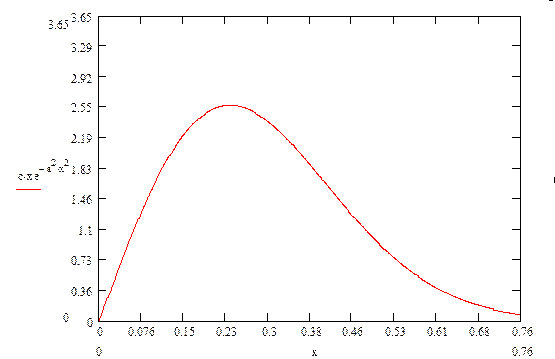
Используя программный  пакет ISW4.0,будем сравнивать полученную выборку с различными  функциями распределения, проверяя при этом вероятность совпадения. Наилучшие результаты получили при сравнении эмпирического наблюдения и распределении  Sb-Джонсона, а именно:

Отношения правдоподобия S=99.918   P=0.34494

Хи-квадрат Пирсона S=89.085   P=0.65163

Колмогорова S=0.35737  P=0.96   

Смирнова S=0.48567  P=0.9    

Омега-малое кв. Мизеса S=0.012994 P=0.96   

Омега-большое кв. Мизеса S=0.10306  P=0.98   

Для иллюстрации приведем следующие графики:

График распределения Sb-Джонсона и эмпирического распределения

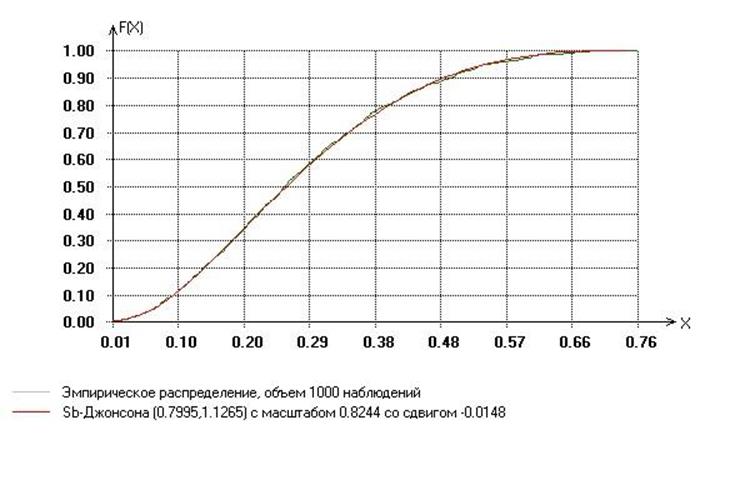
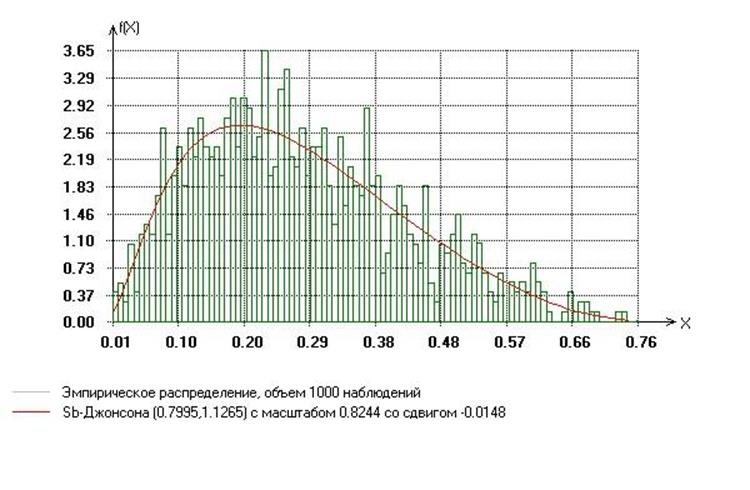
график функции плотности эмпирического распределения и функцией плотности Sb-Джонсона:

в) метод   исключений

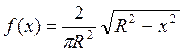
При использовании метода исключений необходимо генерировать две случайные величины , которые подчиняются закону равномерного распределения для получения  каждого значения из выборки.

Найдем  максимум функции f(x):  .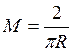

Теперь найдем значения , используя формулы метода

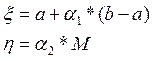
Подставляя значения для нашей задачи, получим

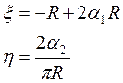
Теперь, генерируя параметры , будем проверять  истинность неравенства: 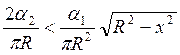. Если неравенство истинно, тогда

 удовлетворяет условиям задачи, если же неравенство ложно, то повторяем  предыдущие действия.

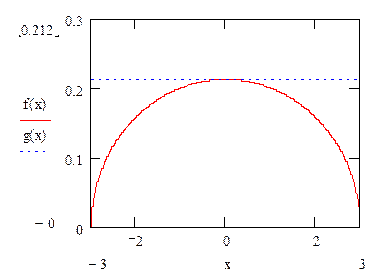
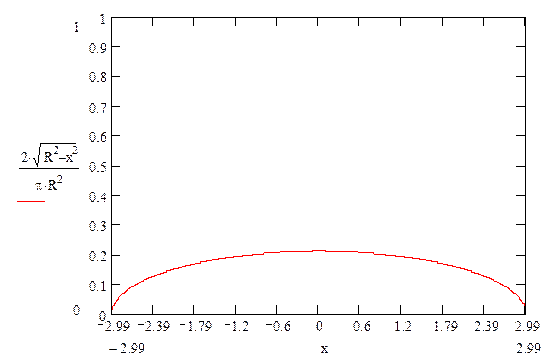
Построим график функции распределения

 

                      

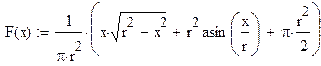
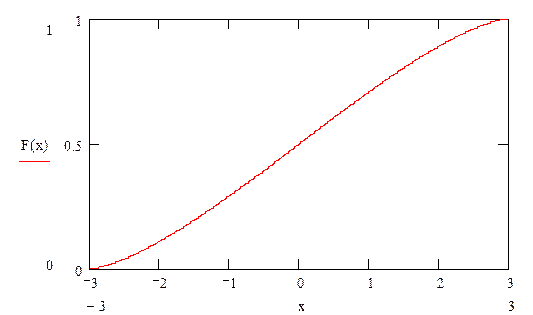
График функции плотности распределения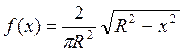

Используя программный  пакет ISW4.0,будем сравнивать полученную выборку с различными  функциями распределения, проверяя при этом вероятность совпадения. Наилучшие результаты получили при сравнении эмпирического наблюдения и распределении  Бета 3-го рода, а именно:

Отношения правдоподобия S=83.157   P=0.78064      

Хи-квадрат Пирсона c попр.Никулина S=82.8     P=0.7889 

Колмогорова S=0.47657  P=0.59    

Смирнова S=0.90848  P=0.8   

Омега-малое кв. Мизеса S=0.029685 P=0.62   

Омега-большое кв. Мизеса S=2e+100   P=0.62     

Для иллюстрации приведем следующие графики:

График распределения Бета 3-го рода  и эмпирического распределения

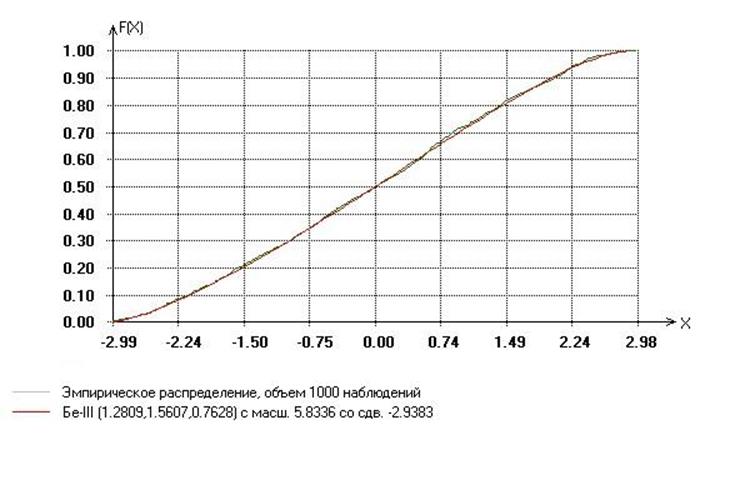
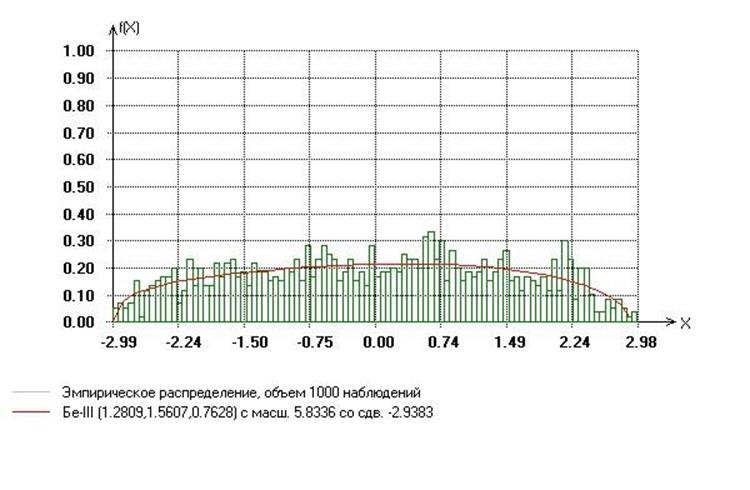
график функции плотности эмпирического распределения и функцией плотности Бета 3-го рода: