






НГТУ
по дисциплине «Моделирование и управление в экономике»
Факультет : ПМИ
Группа : ПМ – 92
Студент : Трубицын Р.М.
Вариант : 21
Преподаватель : Цой Е. Б.
Лабораторная №1
Задание 3
Предложить схему моделирования заданных ситуаций.
Пусть А - событие. Вероятность наступления А равно p.
Если взять ![]() - случайная величина,
то если α<=p,
то событие А произошло.
- случайная величина,
то если α<=p,
то событие А произошло.
если α>p, то событие А произошло.
Можно взять реальный физический пример:
Где событие А – это выпадение одинаковых чисел на 4-х игральных костях. Вероятность события А – p(A)=|A|/|Ω|; 6/(6*6*6*6)=1/216;
Лабораторная №2
Задание 1
Найти методом обратной функции
моделирующее выражение для СВ x,
имеющей заданную плотность распределения: 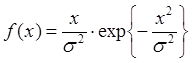 ,
, ![]() .
.
Найдем функцию распределения:
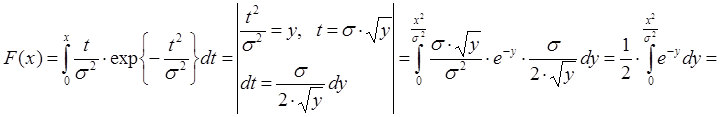
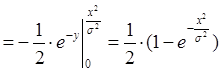
Тогда 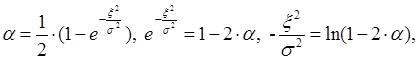 и моделирующая функция для x будет иметь вид
и моделирующая функция для x будет иметь вид ![]()
Задание 2
Найти моделирующее выражение для
СВ x, имеющей заданную плотность
распределения ![]() , по методу обратной функции,
когда j(a)
немонотонна.
, по методу обратной функции,
когда j(a)
немонотонна.
Найдем
константу C из условия 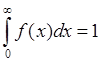 :
:
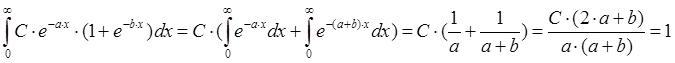
Þ
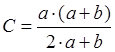
Таким образом,
функция плотности распределения имеет вид: 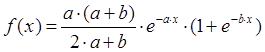 .
.
Положим 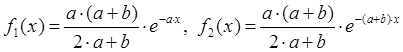 . Вычислим
. Вычислим ![]()
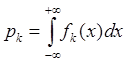 и
и 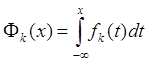 .
.
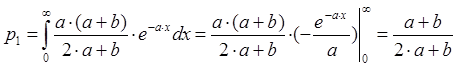
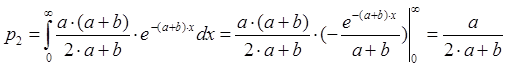
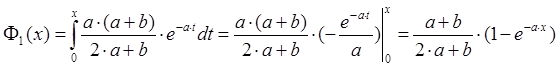
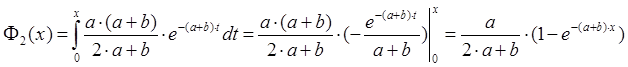
Вычислим
значения границ интервалов: ![]()
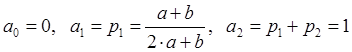 .
.
Вычислим
значения моделирующих функций на этих интервалах (![]() ):
):
1) 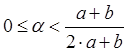
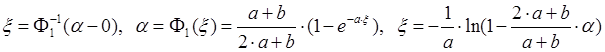
2) 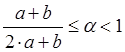
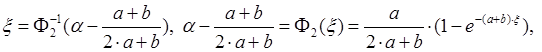
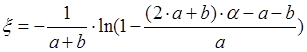
Задание 3
Написать алгоритм моделирования
СВ x, распределенной по закону f(x), с использованием порядковых
статистик. ![]()
В данном случае функция уже
представлена в виде полинома Бернштейна: N=1, b=4, k=1, n=4;
следовательно у нас будет всего одна порядковая статистика с 1 вероятностью –
собственно сама f(x). Т.о. мы
просто перейдем к методу обратной функции: ![]() .
.
Задание 4
Написать алгоритм моделирования случайной величины ε с заданной плотностью распределения. f(x).
![]()
Найдем С по свойству плотности: 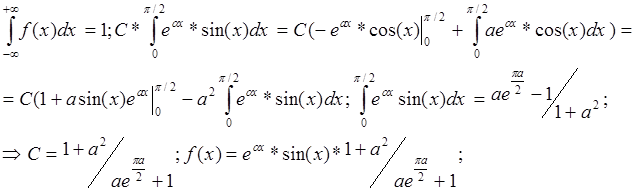
Метод исключения.
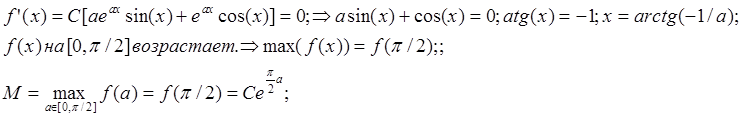
Алгоритм имеет вид:
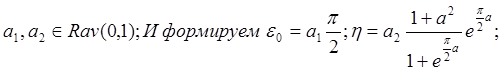
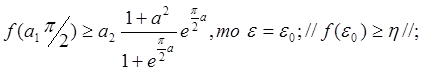 иначе возвращаемся
на шаг 1
иначе возвращаемся
на шаг 1Задание 5
Написать алгоритм моделирования
СВ x при помощи метода суперпозиции, 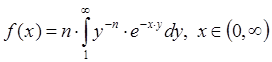 .
.
Для
использования формул 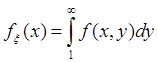 и
и 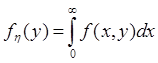 необходимо
найти совместную плотность распределения
необходимо
найти совместную плотность распределения ![]() . Для
заданной плотности распределения она будет иметь вид:
. Для
заданной плотности распределения она будет иметь вид: ![]() ,
находим маргинальное и условное распределения
,
находим маргинальное и условное распределения
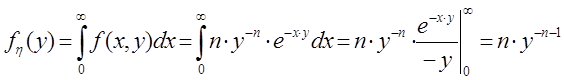 ,
,
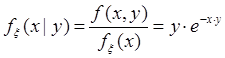 .
.
Тогда имеем
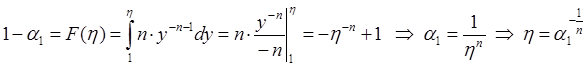
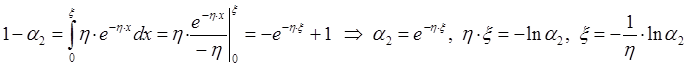 .
.
Используя
суперпозицию, получаем 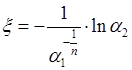 , где
, где ![]() - независимые СВ равномерно распределенные
на (0,1).
- независимые СВ равномерно распределенные
на (0,1).
Алгоритм моделирования:
1) генерируем
![]() ;
;
2) моделируем x в соответствии с полученным моделирующим выражением.
Задание 6
Написать алгоритм моделирования СВ x по методу исключения.
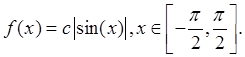 В данном случае M=с;
В данном случае M=с;
тогда: 1 шаг: моделируем ![]()
2 шаг: проверяем
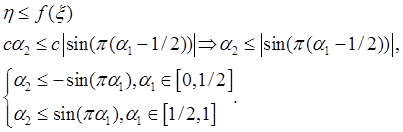
Лабораторная №3
Задание 1
Составить алгоритм моделирования
случайного вектора ![]() имеющего в области c распределение
имеющего в области c распределение ![]() .
.
Воспользуемся стандартным методом:
когда ![]() , тогда в данном случае мы получим:
, тогда в данном случае мы получим:
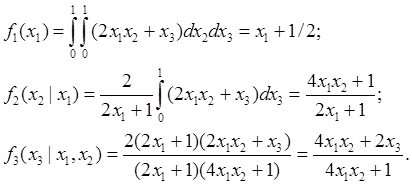
Найдем функции распределения: 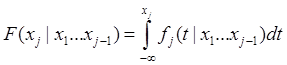 , тогда:
, тогда:
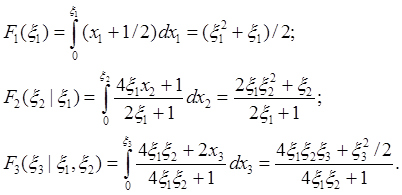
После решения уравнений вида ![]() , мы получим искомый случайный вектор x.
, мы получим искомый случайный вектор x.
Задание 2
Составить алгоритм моделирования
случайного вектора ![]() , имеющего в области
, имеющего в области ![]() распределение
распределение ![]() , по
методу исключения, где
, по
методу исключения, где ![]()
![]()
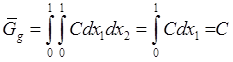
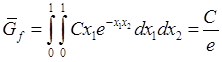
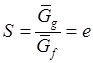
Алгоритм
моделирования вектора ![]() с плотностью
с плотностью 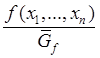 :
:
1.
моделируем ![]() , соответствует
, соответствует 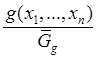 и
и ![]()
2. если ![]() , то выполняем пункт 1., иначе
, то выполняем пункт 1., иначе ![]()
Задание 3
Найти моделирующее выражение для
нормального СВ x с дисперсионной
матрицей 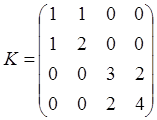 и МО
и МО  .
.
Для моделирования
нормального СВ x используем формулу: ![]() , где
, где ![]() .
Определим элементы матрицы А по формуле
.
Определим элементы матрицы А по формуле 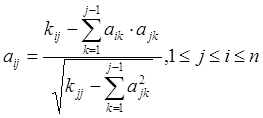 .
.
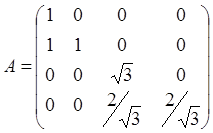 .
.
Тогда ![]()
![]()
![]()
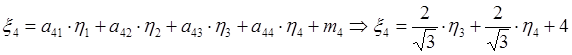
Задание 4
Написать моделирующий
алгоритм одномерного нестационарного гауссовского марковского процесса с
нулевым априорным средними корреляционной функцией вида 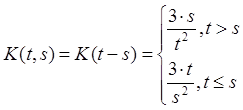 .
.
а) t>s
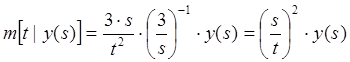 ,
,
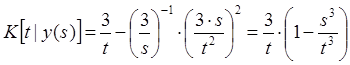 ,
,
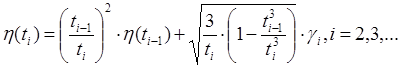 ,
,
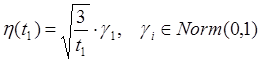 .
.
б) t>=s
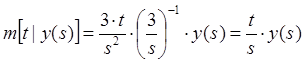 ,
,
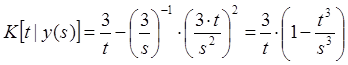 ,
,
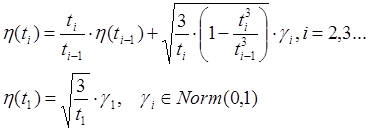 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.