























вычисляется через локальные матрицы жесткости и массы для одномерных конечных элементов.
Вычисление локальной
матрицы массы ![]() :
:
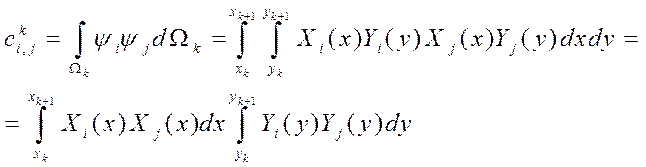 (2.7)
(2.7)
локальная матрица массы для прямоугольных конечных элементов вычисляется через локальные матрицы массы для одномерных конечных элементов.
Таким образом,
для вычисления компонент локальных матриц жесткости ![]() и массы
и массы
![]() на прямоугольных конечных элементах необходимо
предварительно вычислить интегралы вида:
на прямоугольных конечных элементах необходимо
предварительно вычислить интегралы вида:
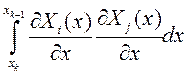 ,
, 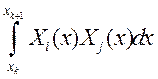 ,
, 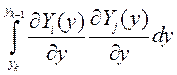 ,
, 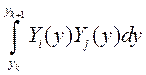 , где X(x) и Y(y) – некоторым образом
определенные на конечном элементе одномерные базисные функции.
, где X(x) и Y(y) – некоторым образом
определенные на конечном элементе одномерные базисные функции.
Локальный
вектор правой части ![]() вычисляется с учетом того, что
функция f на
конечном элементе Wij представлена в виде
разложения по базисным функциям
вычисляется с учетом того, что
функция f на
конечном элементе Wij представлена в виде
разложения по базисным функциям 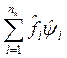 , где
, где ![]() – значения f в вершинах Wij. Тогда
– значения f в вершинах Wij. Тогда ![]() .
.
2.4.Одномерные базисные функции
Рассмотрим вид базисных функций на отрезке [-1,1].
Линейные базисные функции:
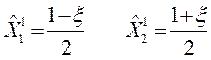 (2.8)
(2.8)
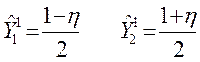
Рассмотрим вид базисных функций на отрезке [0,1].
Линейные базисные функции:
![]() (2.9)
(2.9)
![]()
3.Конечные элементы
3.1. Вычисление одномерных интегралов
Как уже было
сказано выше, для вычисления компонент локальных матриц жесткости ![]() и массы
и массы ![]() на
прямоугольных конечных элементах необходимо предварительно вычислить следующие
интегралы :
на
прямоугольных конечных элементах необходимо предварительно вычислить следующие
интегралы :
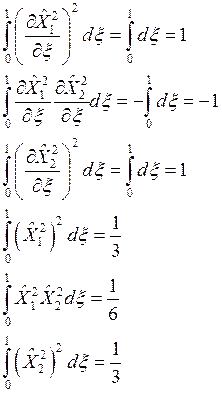 (3.1)
(3.1) 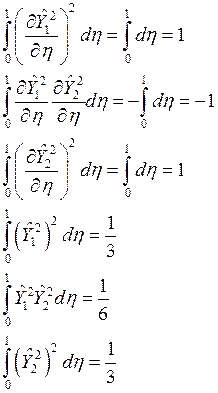 (3.2)
(3.2)
Вычислив одномерные интегралы, можно приступить к вычислению локальных матриц в двумерном случае.
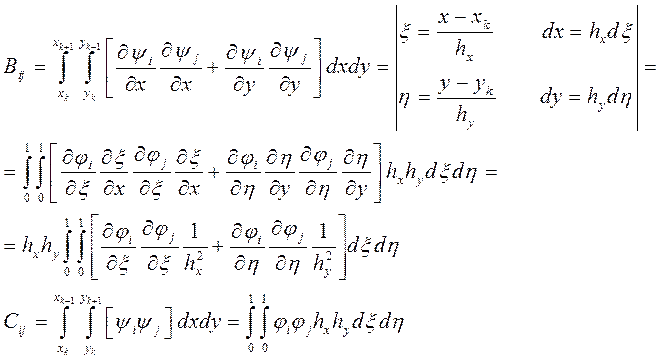 3.2. Вычисления
локальных матриц
3.2. Вычисления
локальных матриц
(3.3)
(3.4)
Таким образом, мы получили вклады в глобальную систему от конечных элементов. Теперь необходимо получить аналогичные вклады от бесконечных элементов.
4. Построение отображения
4.1. Отображение бесконечной области
в конечную область
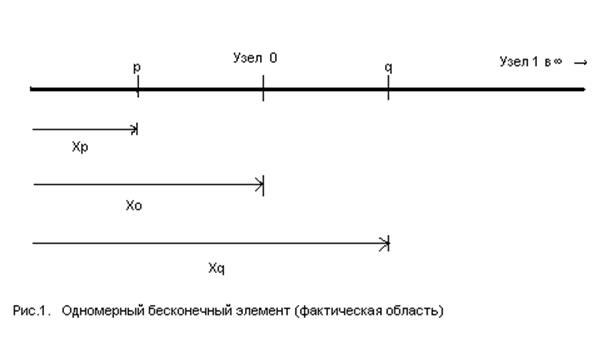
Сначала рассмотрим
возможность отображения одномерной области (или элемента), начинающейся в
некоторой точке с координатой ![]() , содержащей
промежуточную точку с координатой
, содержащей
промежуточную точку с координатой ![]() и продолжающегося до
бесконечности в
и продолжающегося до
бесконечности в ![]() (рис.1), в область
(рис.1), в область ![]() (рис.2).
(рис.2).
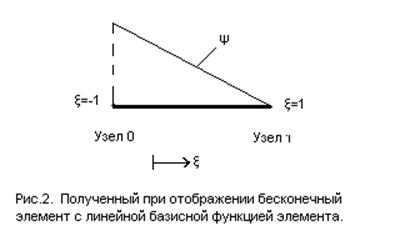
Определим отображение формулой
![]() (4.1)
(4.1)
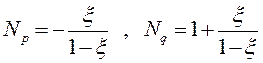 (4.2)
(4.2)
Это параметрическое
отображение специально выбрано таким образом, чтобы данное выражение принимало
бесконечное значение в точке 1 (т.е. при ![]() ) ;
координата
) ;
координата ![]() пока что не определена.
пока что не определена.
Отметим, что в силу формулы (2.1) при ![]()
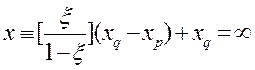 , если
, если ![]() , (4.3)
, (4.3)
а при ![]()
![]() (4.4)
(4.4)
как и требуется; наконец, для точки ![]() которую нужно отобразить в точку
которую нужно отобразить в точку ![]() , мы должны иметь
, мы должны иметь
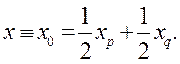 (4.5)
(4.5)
Это соотношение определяет
координату ![]() через
через ![]() и
и ![]() , и мы сразу видим, что точка
, и мы сразу видим, что точка ![]() лежит в центре отрезка
лежит в центре отрезка ![]() .
.
Теперь отображение можно
непосредственно записать через ![]() и
и ![]() как
как
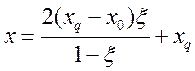 , (4.6)
, (4.6)
и требуемое отображение, таким образом, полностью определено.
Данное соотношение можно разрешить относительно ξ, выразив ξ через х, и, таким образом, обратное отображение определяется соотношением
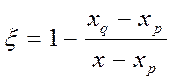 (4.7)
(4.7)
Если одномерное отображение бесконечного элемента найдено, то распространить его на случай двух измерений не составляет особого труда.
4.2.Выбор функций для реализации отображения
Хотя в (4.2) могут быть использованы многие другие виды функций, важно, чтобы выбранные для реализации отображения функции удовлетворяли соотношению
![]() (4.8)
(4.8)
Это условие тождественно выполняется для функций, определенных равенствами (4.2). Необходимость этого условия следует из достаточно очевидного требования, что отображение должно оставаться неизменным при сдвиге начала отсчета х. Иначе говоря, если мы сместим начало отсчета х на ∆х и запишем
![]() (4.9)
(4.9)
то требуется, чтобы для заданного ξ выполнялось равенство
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.