
Критерий х2 несколько иной конструкции используется и в оценке достаточности числа выделенных общих признаков (факторов). Для метода главных компонент расчет xh -критерия осуществляется по формуле Бартлетта:
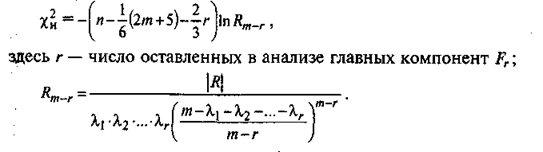
Число степеней свободы для х будет v = 1/2 ((т - г) - т - г -1), наблюденное значение сравнивается с табличным Xa,v и> если %н < Xa,v > принимается предположение о том, что выделенные г главных компонент достаточно полно представляют дисперсию т элементарных признаков и остальные главные компоненты: Fr+i, Ff+2, • •-, Рщ могут в анализе не рассматриваться из-за незначительного уровня их информативности. Если xh >Xo,v» то в анализе для формирования выводов должны быть введены дополнительно другие главные компоненты.
В факторном анализе для проверки гипотезы о достаточности числа обобщенных признаков (факторов) используется %2-критерий Лоули, имеющий аналогичную, как и в предыдущем случае, смысловую нагрузку:
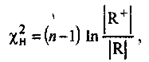
где R+ и \R\ — определители матриц парных корреляций: воспроизведенной (r+=aa'j и исходной.
Критическое значение для х2 -критерия находят по таблицам при заданном уровне значимости а и числе степеней свободы v = l/2\[m-r)2-т-г).Предположение о достаточном числе общих факторов подтверждается, когда xh < Xa,v •
Нередко приложение различных методов факторного анализа на одном массиве данных приводит к весьма отличным друг от друга решениям. При этом возникают вопросы: имеются ли в различных решениях близкие по составу общие факторы и действительно ли существенным образом различаются результаты факторных решений или они идентичны? Соответственно ответам на перечисленные вопросы исследователь в дальнейшем останавливается на любом из имеющихся факторных решений или выбирает из них наилучшее. Для оценки сходства различных факторных решений может использоваться коэффициент конгруэнтности:
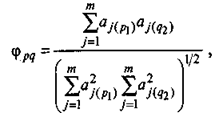
где р и g — сопоставляемые общие факторы соответственно в первом и втором факторных решениях;
aj(p\) и aj(<!2) ~~ коэФФиЦиенты факторных нагрузок на у-и признак (j-\,m) в р- и ^-факторах при первом и втором факторных решениях.
Коэффициент фи изменяется в пределах от —1 до +1. Его значения, близкие к —1, указывают на полную и обратную связь факторов, +1 — связь полную и прямую, наконец, при Фет-»0 следует предположение об отсутствии связи факторов.
Для оценки адекватности факторной модели в целом может использоваться подход, описанный Харманом [90]. К сожалению, он не содержит рекомендаций по поводу пороговых уровней, скажем неадекватности, но в сравнении с другими приемами значительно легче при реализации и базируется на простой средней оценке расхождений исходных и воспроизведенных коэффициентов корреляции:
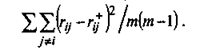
Средний квадрат отклонений Хармана исчисляется по всем, кроме диагональных, коэффициентам корреляции. Из нескольких моделей факторного анализа, естественно, будет лучше та, для которой средняя сумма квадратов отклонений окажется наименьшей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.